水弹性子结构分离及集成方法

邹明松，吴有生

（中国船舶科学研究中心，江苏 无锡 214082）

水弹性子结构分离及集成方法

邹明松，吴有生

（中国船舶科学研究中心，江苏 无锡 214082）

针对船舶结构流固耦合动力学问题，提出将主船体与船内子结构分离，采用聚缩阻抗矩阵综合法获取子结构的聚缩动刚度矩阵，采用声介质中三维结构水弹性方法计及主船体与水介质的流固耦合作用。在此基础上，通过边界协调条件，完成主船体与子结构的集成。该方法提供接口的作用，使得研究成果具有更好的继承性。最后通过一数值算例和一水下结构振动试验，部分验证了方法的正确性和高效性。

水弹性力学；船舶；子结构；模态

1 引 言

随着对海洋工程结构动态设计要求的提高，结构的动态分析变得越来越重要。在复杂结构的动态分析中，由于模型的自由度非常多，不得不进行大量的计算；另一方面，船舶等各种大型海洋工程结构往往是由若干个在不同地方的生产厂家制造的部件（子结构）组装而成，因此，进行各部件独立的动态试验不但更容易，而且也是必须的。动态子结构方法将复杂结构分解成一些较简单的子结构，根据子结构动态特性的计算或试验结果综合出整个复杂结构的动态特性。该方法的理论体系已基本发展成熟[1-2]。

从结构振动特性或者声隐身性能出发，对船内部分子结构（如基座等）进行优化设计，主船体作为弹性边界条件对子结构的振动特性具有较大影响；如将主船体与子结构放在一起建立流固耦合计算模型，则计算量相当大，部分子结构的小量修改将导致整个模型的重新计算，效率低且研究成果继承性不强。针对上述问题，本文提出了水弹性子结构分离及集成方法，该方法具有流固耦合、子结构局部细化等功能特点。

本文是在声介质中三维结构水弹性力学理论[3]的基础上，引入动态子结构的思想，提出了专门用于解决船舶等复杂海洋浮体结构声弹耦合问题的水弹性子结构分离及集成方法。早在20世纪80年代，文献[1]就论述了动态子结构方法在水弹性力学中的应用，其对水介质的处理采用有限区域离散的方法，在大型海洋浮体结构的应用中会面临自由度数过多的问题。随着计算机水平的提升，子结构方法已应用于实船流固耦合动力学分析中[4]。也有众多学者在子结构方法的基础上，提出了各种新的思想。文献[5]将一个复杂的结构分解成主体结构和子结构两部分，主体结构考虑与流体介质的耦合作用，对于刚度、质量分布不确定的子结构采用概率统计的方法处理成模糊子结构（fuzzy structure）。文献[6-7]提出将结构分解成高分辨率的局部子结构和低分辨率的主体结构，建立不同网格尺度的有限元模型或者解析模型进行独立求解和集成。文献[8]提出在进行结构主体振动特性分析时，将结构分解成主体结构和从属结构两部分，对从属结构以及连接边界进行简化处理。本文所述的方法既有动态子结构方法的共性，同时还有水弹性流固耦合分析的特点。

2 水弹性子结构分离及集成方法的基本理论

图1表示一漂浮于水上的船舶结构，其由主船体和基座两部分组成。应用水弹性子结构分离及集成方法将图1所示的船舶结构分割成两部分，如图2所示。不失一般性，采用该模型论述水弹性子结构分离及集成方法的具体内容。

图1 船舶结构示意图Fig.1 Sketch of ship structures

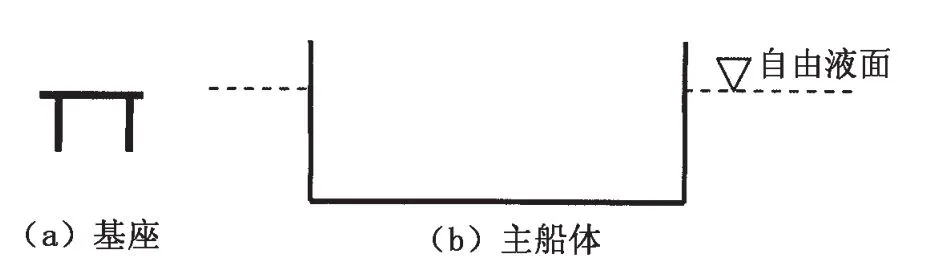
图2 船舶结构的分割Fig.2 Separations of ship structures

在频域内采用动刚度矩阵描述基座结构的振动特性：

上式中：［KB］、［CB］和［MB］分别是基座结构的刚度、阻尼和质量矩阵，ω 为角频率，i为虚数符号。

基座结构的振动方程为：

上式中：｛xB｝为基座结构位移列向量，｛FB｝为作用在基座上的载荷列向量。

求解上述矩阵方程，可得基座外载荷作用点处的位移响应以及主船体的干模态位移主坐标响应。进一步可计算出机械阻抗、水中辐射声等物理量[3]。

实际计算中，如主船体与基座在连接处的网格尺寸不一致，则可以通过插值实现边界连接，这意味着可以建立不同分辨率的主船体和基座计算模型。

3 算 例

采用图3所示的模型作为考核算例进行计算，“主体”是6个面全封闭的，图4是为观察到里面的“子结构”，所以少显示了一个面。具体结构参数为：结构体密度：7 800 kg/m3；杨氏模量：2.1E11 N/m2；泊松比：0.3；干模态阻尼比：0.01。

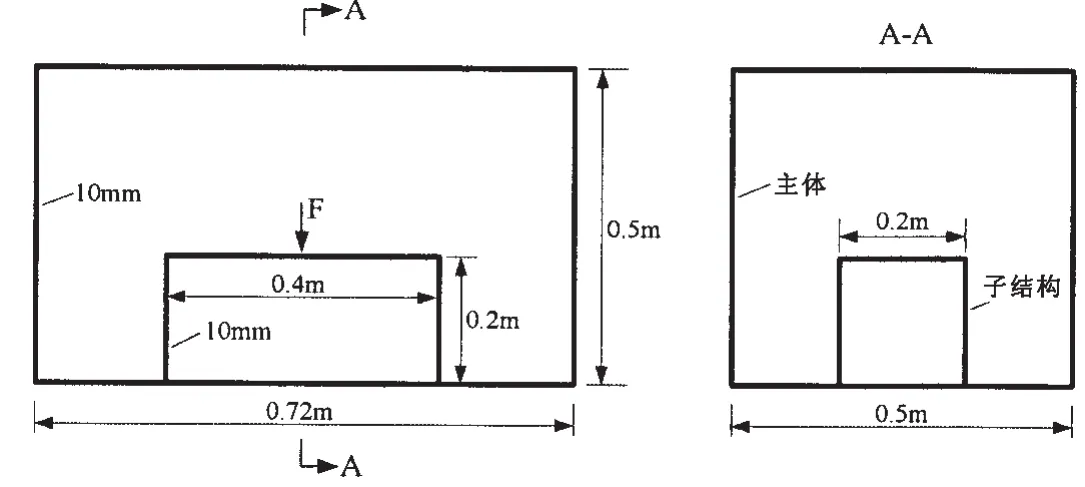
图3 计算模型示意图 Fig.3 Sketch of calculated model

图4 计算有限元模型（壳单元）Fig.4 Calculated finite element model(shell element)

先计算结构在真空中的情况，采用模态叠加法计算结构的谐响应，计算图3所示激励点处（“子结构”中间）的输入机械阻抗，分析模态截断对计算结果的影响。

图5中“直接计算—截断干模态频率1 500 Hz”是指采用模态叠加法计算图4所示有限元模型在激励点处的输入机械阻抗，截断干模态最高固有频率为1 500 Hz；“直接计算—截断干模态频率3 000 Hz”是指截断干模态最高固有频率为3 000 Hz；“子结构法—截断干模态频率1 500 Hz”是指将按照第1节中所述的方法将结构分离成“主体”和“子结构”两部分，“子结构”采用聚缩阻抗方法进行处理，“主体”采用模态展开方法进行处理，其中“主体”截断干模态最高固有频率为1 500 Hz。

通过试算发现“直接计算—截断干模态频率3 000 Hz”已基本收敛到精确值。采用子结构方法之后，“主体”干模态只要截断到1 500 Hz就基本已收敛，这是由于频率较高时“子结构”对其输入机械阻抗存在较大的影响，采用聚缩阻抗方法处理“子结构”不存在模态截断的问题。计算实船中基座等局部结构的机械阻抗时，局部结构本身的细节对计算精度影响很大，往往需要对主船体和局部结构采用不同的网格分辨率进行建模，要求局部结构的模态特性保留得更完备。此时，应用子结构分离及集成方法能大幅度提高效率。

将结构浸没在无限大水介质中，取水介质密度为1 025 kg/m3，水中声速为1 500 m/s。计算结构输入机械阻抗以及单位集中力作用下的水下辐射噪声，结果如图6、7所示。可见：水弹性子结构分离及集成方法具有较高的计算精度；结构水下辐射噪声由结构振动以及振动形态对应的声辐射效率两个因素决定，很多情况下，个别模态虽然对结构振动起到较大贡献，但是对其水下辐射噪声的影响却很小。本算例中，结构在500 Hz以内的辐射噪声主要由干固有频率在1 000 Hz以内的模态提供。

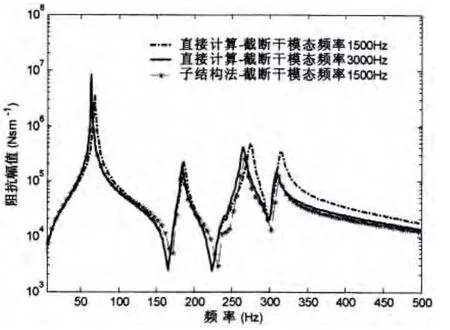
图5 干结构输入机械阻抗Fig.5 Driving-point mechanical impedance of dry structure

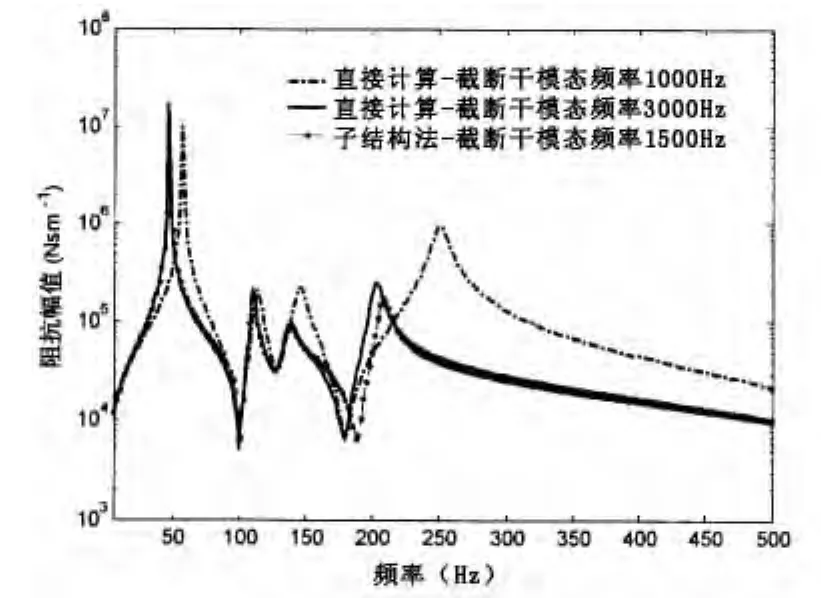
图6 湿结构输入机械阻抗 Fig.6 Driving-point mechanical impedance of wet structure

图7 结构水下辐射噪声（ref 0.67E-18W）Fig.7 Structural acoustic radiation underwater(ref 0.67E-18W)

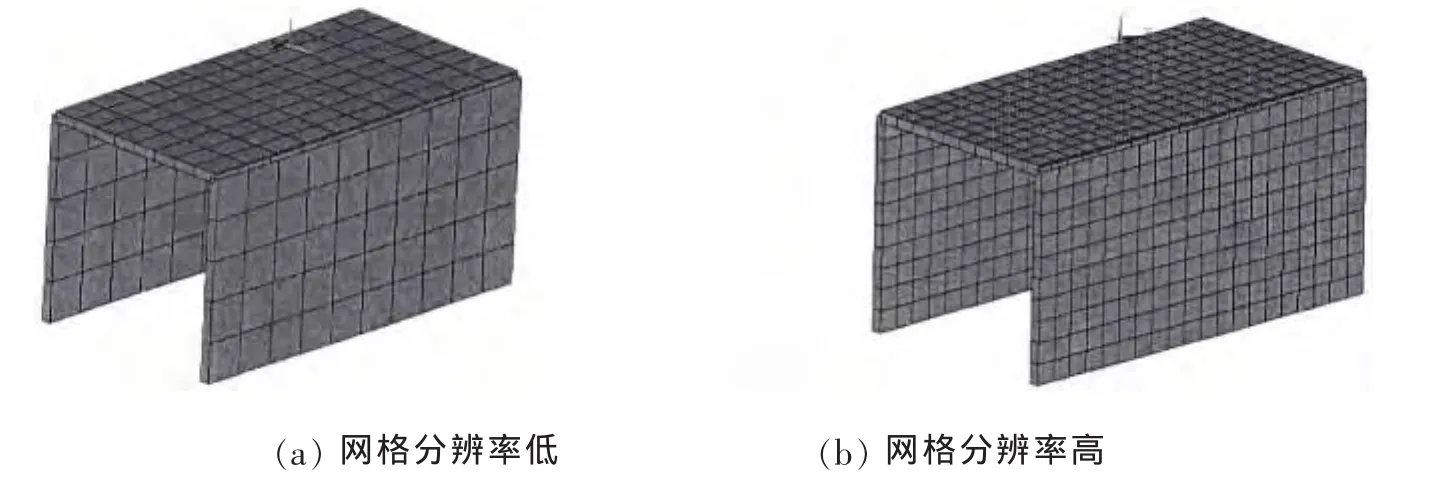
图8 不同网格分辨率的“子结构”计算模型Fig.8 Substructure calculated models with different mesh resolution

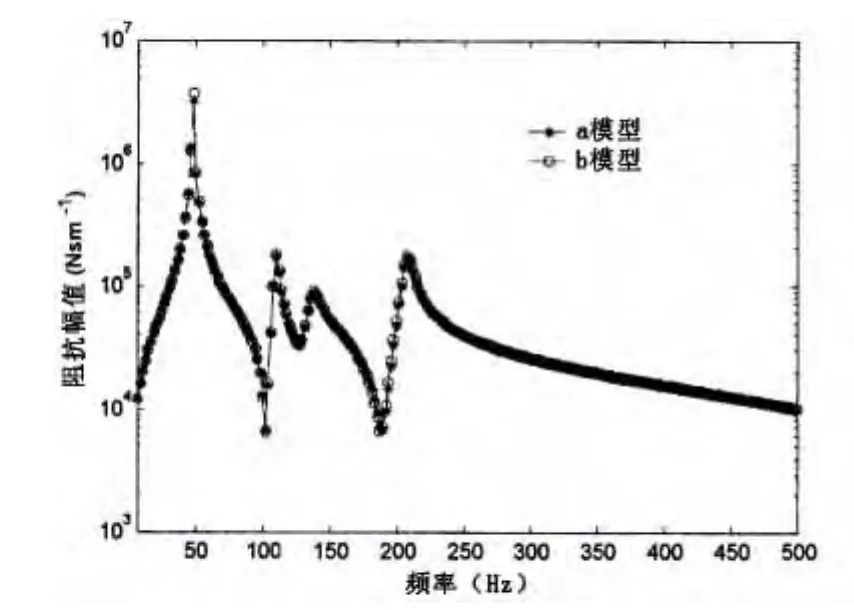
图9 湿结构输入机械阻抗 Fig.9 Driving-point mechanical impedance of wet structure

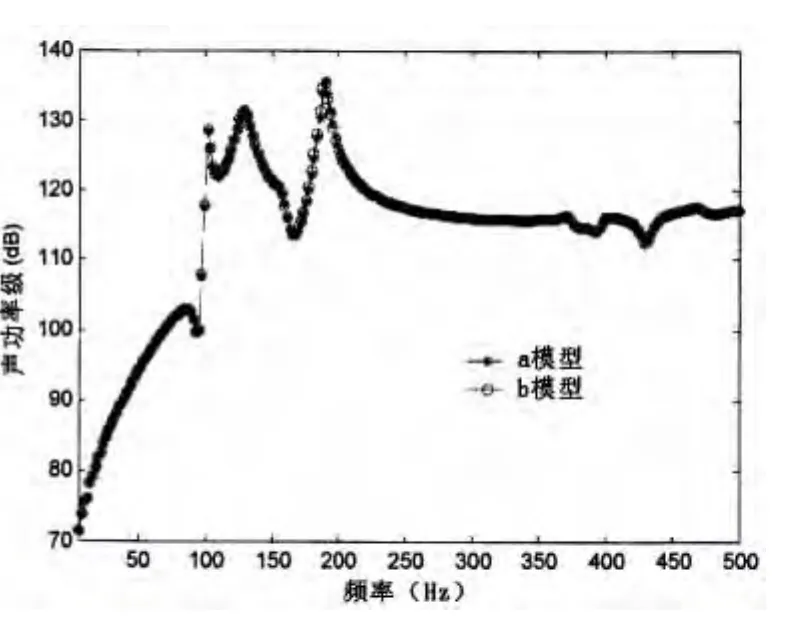
图10 结构水下辐射噪声Fig.10 Structural acoustic radiation underwater

改变“子结构”的网格尺度，如图8所示，“主体”网格尺度不变（同b模型）。应用水弹性子结构分离及集成方法计算两种“子结构”网格尺度模型的阻抗及水下辐射噪声。由图9、10可见：“子结构”采用不同网格尺度的有限元模型，“主体”与“子结构”在连接处网格尺度不一致，对计算结果影响很小。

图11 加筋圆柱壳有限元模型Fig.11 Finite element model of a stiffened cylindrical shell

4 试验验证

开展图11所示加筋圆柱壳结构的水下振动测试试验。试验时，采用电磁激振机垂直激励铺板结构，在激振杆端部安装一个力传感器，获取动态激振力；并在贴近激励点部位安装一个加速度传感器（可认为与激励点重合），测得激励点的垂向加速度响应，通过简单的频谱转化关系可得出速度响应；将测得的转化到频域后的激励力除以速度响应，即得到铺板上激励点处的输入机械阻抗。应用水弹性子结构方法将铺板和主船体分离，再集成计算铺板中部的机械阻抗，与试验结果进行比对，结果如图13所示。

图12 测试时电磁激振机激励铺板Fig.12 The floor-board was excited by an electromagnetic exciter at testing

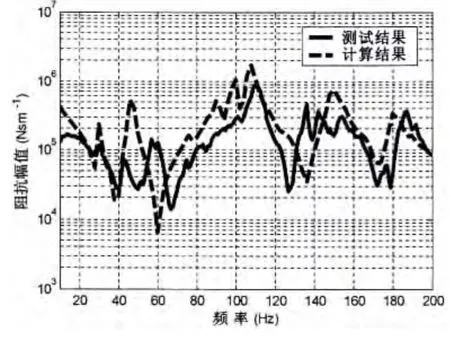
图13 铺板激励点处的输入机械阻抗Fig.13 Driving-point mechanical impedance of the floor-board

5 结 论

本文将子结构思想与水弹性理论相结合，提出了水弹性子结构分离及集成方法，通过数值算例和实物试验，部分验证了方法的正确性和高效性。

在船舶结构流固耦合分析中，应用水弹性子结构分离及集成方法可以针对主船体和船内局部结构建立不同分辨率的计算模型，该项功能使得在保证计算精度的同时减小了计算量，也进一步提高了实船建模的可操作性。从一般单位的中小型计算机计算能力以及实际工程应用的角度出发，本文所述的方法还可以提高计算频率范围。

在主船体固定的情况下，应用本文所述的方法可以方便且高效地修改局部结构进行计算分析、优化迭代。

发展一种船舶结构参数化建模的技术，将提升现有的各种计算方法以及计算软件的工程实用化水平。本文提出的将主船体与子结构分离，且在集成时主船体与子结构在边界连接处可以有不同网格尺度的方法减小了船舶局部结构参数化建模的技术难度。

[1]王文亮,杜作润.结构振动与动态子结构方法[M].上海:复旦大学出版社,1985.

[2]殷学纲,陈 淮等.结构振动分析的子结构方法[M].北京:中国铁道出版社,1991.

[3]邹明松,吴有生等.考虑航速及自由液面影响的声介质中三维结构水弹性力学研究[J].船舶力学,2010,14(11):1304-1311.Zou Mingsong,Wu Yousheng,et al.Three dimensional hydroelasticity with forward speed and free surface in acoustic medium[J].Journal of Ship Mechanics,2010,14(11):1304-1311.

[4]邹春平,陈端石等.船舶结构振动模态综合法[J].上海交通大学学报,2003,37(8):1213-1218.

[5]Soize C.A Model and numerical method in the medium frequency range for vibroacoustic predictions using the theory of structural fuzzy[J].J Acoust.Soc.Am.,1993,94(2):849-865.

[6]Franzoni L P,Park C D.An illustration of analytical/numerical matching with finite-element analysis for structural vibration problems[J].J Acoust.Soc.Am.,2000,108(6):2856-2864.

[7]Park C D.Analytical-numerical matching for fluid-loaded structures with discontinuities[J].J Acoust.Soc.Am.,2004,116(5):2956-2968.

[8]Liang J,Petersson B A T.Dominant dynamic characteristics of built-up structures[J].J Sound Vib.,2001,247(4):703-718.

A method used for separating and coupling substructure based on hydroelasticity theory and dynamic substructural theory

ZOU Ming-song,WU You-sheng
(China Ship Scientific Research Center,Wuxi 214082,China)

Aiming at the fluid-structure coupling dynamic problems of ship structure,the ship structures are separated into main hull and substructure in ship.The reduced dynamic stiffness matrix of substructure is obtained by using reduced method of impedance matrix synthesis,and the fluid-structure coupling effect of main hull with water is considered by using 3-D hydroelasticity analytical method in acoustic medium.On that basis,the coupling of main hull and substructure is implemented through compatible boundary condition.This method provides joint function that makes research productions have better succession.The validity and high efficiency of this method are checked partly through a numerical calculation and a vibration underwater test of a floating body.

hydroelasticity;ship;substructure;modal

TV131.2

A

10.3969/j.issn.1007-7294.2014.05.012

1007-7294（2014）05-0574-07

2014-01-03

邹明松（1982-），男，中国船舶科学研究中心博士研究生，工程师，E-mail：zoumings@126.com；

吴有生（1942-），男，研究员，博士生导师，中国工程院院士。