大型集装箱船高强度钢甲板裂纹缺陷的安全寿命评估

张 鼎 ，黄小平 ，丁仕风 ，洪 英 ，徐博文

（1上海交通大学 海洋工程国家重点实验室，上海 200240；2中国船舶及海洋工程设计研究院，上海 200011；3中国船级社 上海规范研究所，上海 200135）

大型集装箱船高强度钢甲板裂纹缺陷的安全寿命评估

张 鼎1，2，黄小平1，丁仕风3，洪 英3，徐博文3

（1上海交通大学 海洋工程国家重点实验室，上海 200240；2中国船舶及海洋工程设计研究院，上海 200011；3中国船级社 上海规范研究所，上海 200135）

文章根据船级社规范的疲劳校核应力计算方法及应力范围长期分布的基本特征，采用等效应力法将船舶受到的外载荷转换为等幅疲劳载荷。将失效评估图技术和疲劳裂纹扩展计算方法结合起来，探讨复杂载荷作用下集装箱船高强度钢甲板安全寿命评估方法，并考虑焊接残余应力的影响。对某大型集装箱船上甲板焊接接头焊趾处裂纹缺陷在复杂载荷作用下的疲劳寿命进行了评估，其中考虑了表面裂纹缺陷和埋藏裂纹缺陷两种情况。结果表明，初始裂纹的尺寸大小对裂纹扩展影响显著，且在相同的初始裂纹尺寸和外载荷条件下，表面疲劳裂纹对结构安全的危害性比内部的埋藏裂纹危害性更大。

高强度厚钢板；失效评估图技术；裂纹缺陷；单一曲线模型；应力范围；寿命评估

1 引 言

大型集装箱船具有长大开口、方型系数小、剖面变化显著和明显艏外飘以及高航速等特点，为减轻船体自重，上甲板等结构构件大量采用高强度厚钢板，其疲劳问题更为突出需要加以重视。在交变载荷作用下，经常在接头的薄弱部位（焊趾处）存在或萌生疲劳裂纹。并且焊接结构中的疲劳裂纹大多起源于焊接接头表面几何不连续引起的应力集中处，少数起源于焊缝的内部较大的焊接缺陷。在循环应力作用下，这些疲劳裂纹开始扩展，当其达到临界尺寸、构件剩余断面不足以承受外载荷时，裂纹突然发生没有明显塑性变形的失稳扩展至断裂。因此，对集装箱船上甲板的焊接缺陷部位进行安全寿命评估很有必要。失效评估图（FAD）技术作为一种含缺陷结构的安全评定方法，由于其简便又不失安全的性能，在输油管道、压力容器等工程领域中被广泛采用[1-3]。但是将失效评估图技术运用于船舶结构的安全寿命评估则少见报道。且国内船舶与海洋工程界开展的基于疲劳裂纹扩展预报方面的工作主要是基于Paris裂纹扩展率模型[3-6]，但是由于Paris公式没有考虑裂纹扩展门槛值和平均应力等因素的影响，故不能有效预测随机载荷作用下结构的疲劳裂纹扩展行为。而黄小平等[7-10]提出的裂纹扩展率单一曲线模型能考虑这些因素的影响并且可直接使用Paris公式中的材料常数，有较好的工程适用性。鉴于此，本文主要做了以下工作：（1）介绍了BS7910给出的缺陷评估分级方法及失效评估图技术的基本思路；（2）将应力范围的长期分布服从两参数Weibull分布的随机载荷转换为等效疲劳载荷，裂纹扩展率采用单一曲线模型，结合焊趾裂纹缺陷应力强度因子和参考应力及残余应力引起的应力强度因子的计算方法计算裂纹随时间的变化，结合失效评估图技术，探讨了复杂载荷作用下集装箱船高强度钢甲板裂纹随时间的变化与安全寿命的关系和计算评估方法；（3）分别对某大型集装箱船上甲板焊接接头处常见的表面裂纹缺陷和埋藏裂纹缺陷在复杂载荷作用下的疲劳寿命进行了评估。

2 缺陷评估原理和方法

2.1 缺陷的评估等级

失效评估图考虑了从脆性断裂到塑性失稳所有可能的破坏行为，被认为是一种最有效且最可靠的含平面型缺陷结构完整性评价的方法。BS7910[11]给出了缺陷的三种断裂评估等级。第一级评估是简化的评估路线，当材料性能、施加应力等信息有限时，使用其保守的估计值。第一级评估分为Level 1A和Level 1B两种方法，其中Level 1A方法使用了失效评估图；Level 1B是不使用失效评估图的手工估算方法。第一级评估方法包含一个平均值为2的内在安全因子来修正缺陷尺寸，因此不需要另外的部分安全因子。

第二级评估是应用较多的评估路线，有Level 2A和Level 2B两种方法，两种评估方法都使用失效评估图，但都不包含内在安全因子，因此需要确定合适的部分安全因子。Level 2A的FAD具有普适性，而Level 2B的FAD是依据具体材料的应力—应变曲线导出的，因此Level 2B评估一般比Level 2A精确，但不适用于焊缝热影响区材料。

第三级评估则更为精确，适合于稳定撕裂的延性材料，分为Level 3A、Level 3B和Level 3C三级，每种评估方法均使用各自的评估线，并且都进行延性撕裂分析，该分析所需要的材料断裂韧度数据的形式是裂尖张开位移δ或J积分阻力曲线。Level 3A评估不需材料的应力—应变曲线，而是使用了Level 2A评估普遍适用的FAD；Level 3B评估的FAD是依据具体材料的应力—应变曲线导出的；Level 3C评估的FAD是通过对具体材料和几何的缺陷结构进行弹性和弹塑性分析求出Je和J积分得到的。

2.2 失效评估图技术

本文采用Level 2A进行评估，其评估图如图1所示。如果评估点位于失效评估曲线内，就可以认为裂纹是合格的；若位于失效评估曲线上或曲线外，则判定其为不合格。这种评估方法最大的优点是同时考虑了断裂韧度和强度因子两种因素对缺陷结构安全性的影响。

（1）失效评估曲线

Level 2A的失效评估曲线是一条通用失效评定曲线，该曲线对于应力—应变曲线上无明显的屈服平台的所有材料都是适用的，它不要求提供应力—应变关系曲线，例如对于热应力影响区HAZ，就可按照此曲线进行评估。其中，失效评估曲线方程为[11]：

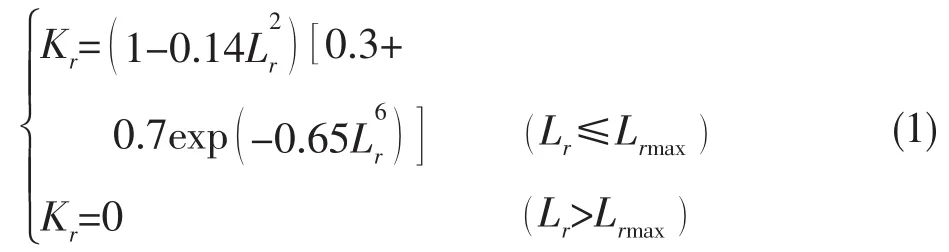
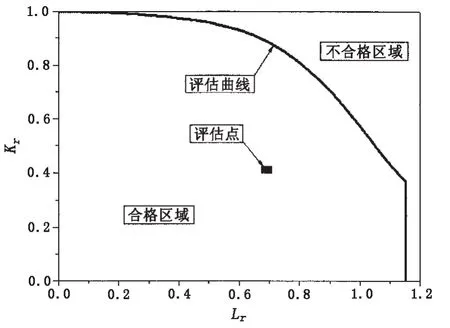
图1 Level 2A失效评估图[11]Fig.1 Failure assesment diagram of Level 2A

式中：Kr为断裂参数，Lr为塑性失稳参数。

（2）断裂参数Kr的计算方法

断裂系数Kr为应力强度因子与材料的断裂韧度的比值，即

式中：σref为参考应力；σfs为缺陷处材料的流动强度，取材料屈服强度和拉伸强度的平均值，不超过1.2倍的屈服强度。

3 集装箱船高强度钢甲板安全寿命评估方法

安全寿命评估应能针对船舶在整个服役期内任意阶段的裂纹进行安全性和剩余寿命预报和评估，从而根据对存在裂纹结构的安全寿命评估结果决定科学的检维修周期。因此，存在裂纹类缺陷船舶结构的安全评估的关键之一是在船舶服役环境载荷下的裂纹扩展预报，其次就是根据预报结果进行安全性评估。

3.1 疲劳载荷计算

3.1.1 疲劳校核应力计算方法

名义应力（σn）定义为：在结构构件中考虑宏观几何影响，但不计由于结构不连续和焊缝存在引起的应力集中的应力。热点应力（σh）定义为：在热点处，考虑由于细部几何形状引起的结构不连续的影响，但不包括焊缝影响的局部应力。疲劳校核需要垂直于目标裂纹的主应力，因此应选取垂直于目标裂纹的一系列单元将主应力插值到目标裂纹处。根据DNV规范，选用垂直于目标裂纹45°范围内的主应力，作为疲劳校核主应力，热点应力则是通过距校核点0.5t与1.5t处单元表面上最大主应力向外插值求得[12]。

在计算疲劳热点的应力幅值时，需要进行应力组合。应力成分由三部分组成，分别是垂向弯矩作用下的热点应力值 （σv）、水平弯矩作用下的热点应力值 （σhg）及扭矩作用下的热点应力值 （σwt+ σgt）。DNV

规范给出了热点应力范围（Δσh）及名义应力范围（Δσn）计算方法[12]：

式中：K为应力集中系数，本文取1.0[12]。

3.1.2 应力范围的长期分布

在船舶结构疲劳分析中，经常用两参数的Weibull分布来表示应力范围Δσ的长期分布，其概率密度函数为[13]：

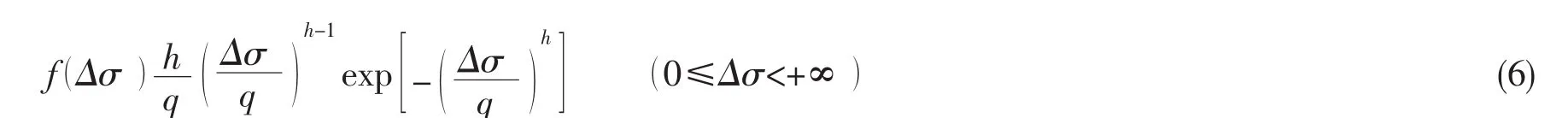
式中形状参数h由主尺度来确定，到目前的研究结果表明[13]，形状参数的取值一般是在0.7-1.3之间。而尺度参数q可用回复期内疲劳载荷长期分析得到的对应某一超越概率的应力范围表示。本文采用以下方法计算这两个参数[12，14]：

其中：L 为船长，（m）；D 为型深，（m）；d1为计算工况下的吃水，（m）；z为计算点距基线的高度，（m）；当计算点在横舱壁上时，f=0.92；n0为疲劳载荷谱的回复期。

3.1.3 等效应力法

等效应力法的目标是寻求典型载荷谱段的等效应力，以便将该谱段转换成一恒幅载荷谱，进一步简化计算。转换后恒幅载荷谱的等效应力可写为[15]：

式中：σi和ni分别为典型载荷谱段中载荷水平i所对应的应力（最大应力、最小应力或应力幅）和循环次数。α=2时，等效应力即为通常采用的均方根应力。

本文采用等效应力范围计算疲劳寿命，根据（6）式产生应力范围满足Weibull分布的随机数列，然后基于（10）式得到等效应力范围，将已生成的随机载荷序列转换成恒幅载荷谱，计算相应的应力强度因子范围等。

3.2 裂纹扩展率模型

黄小平等[7-10]提出了单一曲线模型的概念，这是一个由裂纹扩展率单一曲线和相应的等效应力强度因子幅组成的裂纹扩展预报模型，明确了随机载荷作用下的裂纹扩展率曲线采用R=0时的裂纹扩展率曲线，同时将平均应力和载荷时程效应的影响表达出来，对BS7910推荐的三段扩展率公式，在单一曲线模型中只需用一个方程就能很好地表达。并将单一曲线模型应用于多种结构钢的疲劳寿命预报问题，结果表明此模型有较好的工程适应性。其基本表达式为：其中：ΔKeqo，ΔKtho为等效于应力比R=0时的等效应力强度因子幅和应力强度因子幅门槛值，（MPa）；C为Paris系数，m为裂纹扩展指数；MR为载荷比的修正因子；β，β1为决定于材料和使用环境的参数；Kres为残余应力引起的应力强度因子；MP为载荷次序的修正因子，不考虑超载的影响时MP=1，考虑载荷次序影响时，MP的计算公式参见文献[9]。

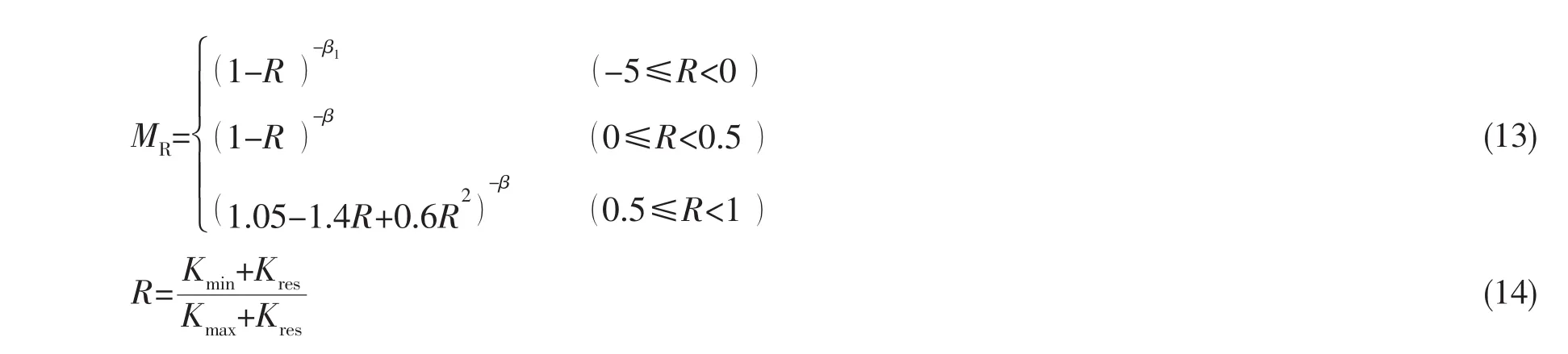
3.3 焊趾处裂纹缺陷的应力强度因子和参考应力计算

3.3.1 表面裂纹缺陷

表面裂纹是船舶结构常见的缺陷形式之一，在确定其应力强度因子时，一般将其简化为半椭圆裂纹。平板表面裂纹应力强度因子有成熟的计算方法，且以Newman-Raju[16]提出的表面裂纹应力强度因子计算式最有代表性。焊趾表面裂纹在拉伸、弯曲应力作用下的应力强度因子可以按照下式计算[17]：

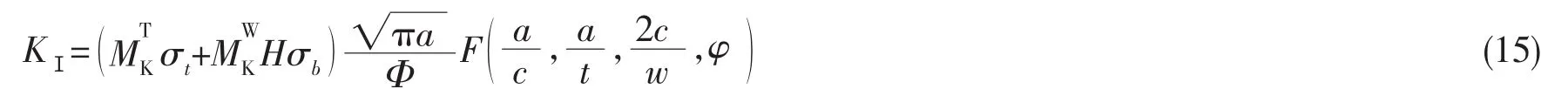
其中：KⅠ为只考虑Ⅰ型裂纹的应力强度因子；σt为拉应力；σb为弯曲应力；a为裂纹深度；c为裂纹半长；t为板厚；w为板宽；为拉伸应力下焊接结构应力强度因子增大正系数；为弯曲应力下焊接结构应力强度因子增大正系数；适用范围：0＜a/c≤1.0，0＜a/t≤1.0，2c/w≤0.5，0≤φ≤π。 具体的表达式参见文献[17]。

当缺陷或裂纹位于局部应力集中区时，在计算KⅠ时必须考虑应力集中场的影响，对于焊趾表面裂纹来说，应力强度因子放大系数MK是裂纹尺寸，接头的几何参数以及载荷的函数。正常情况下，随着裂纹深度的增加，MK的值从等于无裂纹时的应力集中系数减小到1.0。本文采用文献[18]给出的对接接头的MK计算方法，其结构简图如图2所示。

缺陷评估的参考应力值σref是引起结构塑性破坏的所有可能的应力之和的最大可能值，BS7910附录P给出了各种缺陷参考应力的计算方法。对于表面裂纹，参考应力的计算公式为[11]：

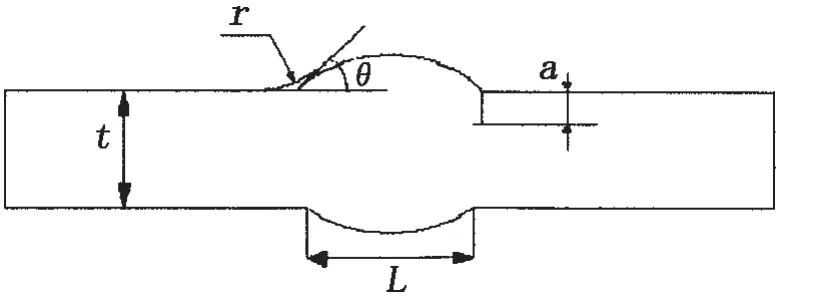
图2 对接接头简图Fig.2 Sketch of weld joint

式中：Pm为薄膜应力，Pb为弯曲应力。

3.3.2 埋藏裂纹缺陷

埋藏裂纹是厚钢板焊接结构中另一种常见的缺陷存在形式，在实际运用中一般将其简化为椭圆裂纹。BS7910给出了埋藏椭圆裂纹在拉伸载荷作用下的应力强度因子经验表达式[11]：

式中：KⅠ为只考虑Ⅰ型裂纹的应力强度因子；σt为拉应力；a为裂纹深度半长；c为裂纹长度半长；t′为板的等效厚度，等于2a+2p；w为板宽。详细的计算表达式见BS7910附录M，且本文分析的埋藏裂纹中心位于板厚 0.5t处，如图 3 所示。 上式适用范围：0≤a/2c≤1，2c/w＜0.5，-π≤φ≤π，且当 0≤a/2c≤0.1 时，a/t′＜0.625（ 0.6+a/ ）c 。

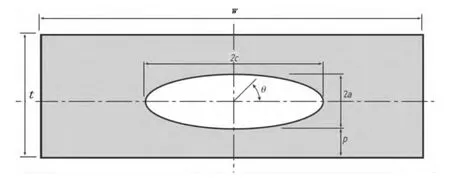
图3 埋藏裂纹示意图Fig.3 Schematic diagram of embedded crack

其中，埋藏裂纹缺陷参考应力的计算公式为[11]：

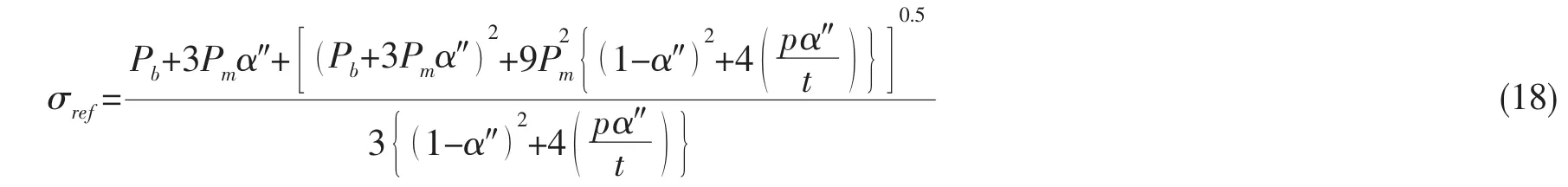
3.4 焊趾处焊接残余应力的应力强度因子计算

在焊接结构加工过程中，由于焊接热循环的作用，引起接头局部不均匀的热塑性变形和相变，产生了自相平衡的残余应力，残余应力的分布和变化非常复杂。文献[17]建议垂直焊缝方向的焊接残余应力在焊趾处表面的取值为：

式中：σR为残余应力，（MPa）；σY为材料的屈服强度，（MPa）。当保守计算时，可认为残余应力沿壁厚均布且等于表面处的残余应力。对于残余应力引起的应力强度因子的计算，借用Newman-Raju[16]公式的拉应力部分，将残余应力简单地视为拉应力即可，故残余应力的应力强度因子计算式可如下表示：

4 实例分析

某大型集装箱船总长334 m，垂线间长320 m，设计型宽42.8 m，设计型深24.8 m，设计吃水13.0 m。其中，上甲板两侧的甲板条宽均为2.2 m，板厚达到68 mm，其材料为高强度钢EH36，最小屈服强度为355 MPa，抗拉强度为490 MPa，断裂韧度的估计值Kmat=102 MPa（设计温度为0°C）[19]。此集装箱船中部上甲板有一对接焊接头，其焊缝焊趾处存在裂纹缺陷，该结构受到波浪随机载荷作用。

4.1 目标甲板焊趾处疲劳校核应力计算

4.1.1 疲劳热点有限元模型

本文选取的研究对象为船中右舷处上甲板，其位置如图4所示，疲劳校核的热点部位为目标甲板中部焊接区域。图5为目标甲板粗网格有限元模型，作为疲劳分析的前期准备，对模型进行了细化，有限元校核点附近的网格尺寸为t×t，延伸至10～15倍t×t的范围，如图6所示。并将此细化模型直接嵌入整船模型中一同进行分析。

波浪载荷的计算是基于整船结构分析所采用的设计波方法，具体的计算过程参见文献[20]。对于甲板，设计波主要载荷参数是垂向波浪弯矩[21]。其中，计算工况为：波浪工况为迎浪工况，对应中横剖面垂向波浪弯矩最大；静水工况为满载工况。疲劳载荷所对应的超越概率水平取10-4（即回复期n0=104）。选取的海况分布资料为北大西洋海浪散布图。

图4 整船有限元模型Fig.4 Finite element model of global ship

图5 目标甲板粗网格有限元模型Fig.5 Coarse finite element model of target deck

图6 目标甲板细网格有限元模型Fig.6 Fine finite element model of target deck

图7 目标甲板主应力分布云图Fig.7 The diagram of principal stress distribution of target deck

4.1.2 名义应力计算

图7为上述工况下的目标甲板主应力分布云图，根据上文介绍的疲劳校核应力计算方法，可以得到校核点的最大热点应力为131.8 MPa。同时，由于选取的计算工况中垂向波浪弯矩最大，其他波浪矩为0，根据（4）式可以得到回复期n0=104时的最大热点应力范围Δσh0=0.9σv=118.62 MPa。由于拉伸应力对疲劳裂纹扩展的贡献很大，其它形式的应力影响很小，可以忽略不计，故本文的裂纹扩展预报只考虑拉伸应力的作用，且采用名义应力法进行计算。由（5）式给出的热点应力和名义应力转化公式，可以得到结构处的最大名义应力范围Δσn0=Δσh0=118.62 MPa。然后根据（7）-（9）式计算得到名义应力范围的Weibull分布形状参数h=0.811，尺度参数q=7.676。

在回复期取得足够长的条件下，长期分布是不变的，即Weibull分布的两个参数不随回复期大小的变化而变化[13]。这样，若认为n0=104和n1=107都是足够长的回复期，则可认为它们对应的长期分布是相同的，即有：

式中：Δσn0和Δσn1分别为对应与超越概率10-4和10-7的名义应力范围。则超越概率10-7对应的最大名义应力范围Δσn1=236.5 MPa，最大名义应力由（4）式和（5）式得σn1=262.78 MPa。

4.1.3 等效载荷谱及应力强度因子计算

由上述计算分析可知，名义应力范围Δσn1的Weibull分布概率密度函数为：

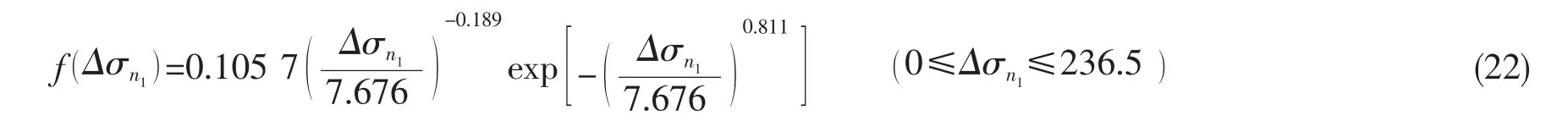
在此基础上，本文分析了目标甲板在回复期n1=107内的疲劳裂纹扩展情况。根据表达式（22），利用数学软件工具Matlab产生107个服从Weibull分布的随机数据，每个数值即为每个循环对应的名义应力范围Δσn1，其概率分布如图8所示。由于数量较多，只列举了其中200个名义应力范围的分布情况，如图9所示。然后将这些随机数列转化成恒幅载荷谱，根据（10）式计算得到等效名义应力范围（均方根应力）Δσn1=13.90 MPa， 故载荷谱中的最大应力 σmax=σn1=262.78 MPa， 最小应力 σmin=σmax-Δσn1=248.88 MPa。由于本文只考虑拉伸应力的作用，故载荷循环应力中的最大拉伸应力σtmax=σmax，最小拉伸应力σ=σ ，其中，考虑残余应力的影响时，载荷比R=。计算参考应力时，本文取薄膜tminmin应力Pm=σtmax，弯曲应力Pb=0。且计算断裂系数时，一次应力为最大拉伸应力σtmax，二次应力为焊接残余应力σR，塑性修正因子ρ=0。计算过程中，单一曲线模型参数为：C=5.32×10-11，m=3。

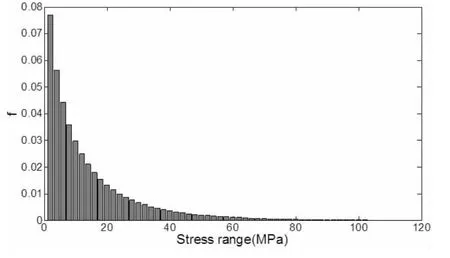
图8 名义应力范围概率分布图Fig.8 Probability distribution of nominal stress range

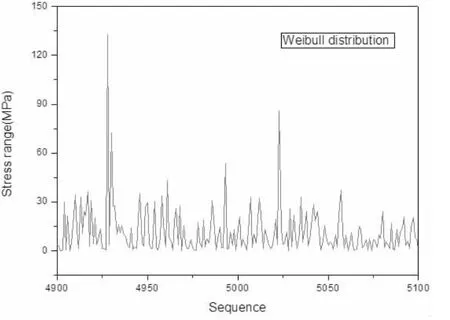
图9 名义应力范围分布Fig.9 Distribution of nominal stress range

4.2 预报结果安全评估分析

由于表面裂纹和埋藏裂纹是焊接接头处常见的裂纹存在形式，本文分别对目标甲板对接接头处以上两种裂纹缺陷在上文得到的随机载荷作用下的疲劳寿命进行了评估。Yoichi等[22]对船用高强度厚钢板进行了防脆断分析，基于船体建造无损检测的经验及安全角度，建议厚钢板初始缺陷裂纹的深长比（a0/c0）为0.2，且由于焊趾裂纹多为同时多处萌生，初始裂纹长度c0应该取得较长。两种寿命评估情况均选择了以下三种初始裂纹尺寸组合：a0=4 mm，c0=20 mm、a0=4.25 mm，c0=21.25 mm和a0=4.5 mm，c0=22.5 mm，深长比均为0.2，且结构所受外载荷相同。在初始裂纹的基础上给出一定裂纹尺寸的增量，采用裂纹长度和深度同时扩展的机制，根据单一曲线模型裂纹扩展率公式求出一定寿命下的裂纹增量，将计算得到的一系列寿命下的裂纹进行安全性评估。其中，失效评估点为裂纹深度方向尖端点。

图10-12分别为三种初始裂纹尺寸组合对应的表面裂纹缺陷失效评估图，从图中可以看到，初始裂纹深度a0和长度c0的取值越大，载荷循环过程中得到的评估点曲线越靠近FAD曲线。当初始裂纹尺寸的取值较大时，由上文裂纹扩展率公式及应力强度因子和参考应力计算公式可知，裂纹深度方向扩展速率较快，且深度尖端应力强度因子和参考应力的值较大，故完成相同的载荷循环次数后，断裂参数和塑性失稳参数均较大。且当初始裂纹尺寸组合为a0=4.5 mm，c0=22.5 mm时，载荷循环到一定次数后，评估点曲线已超越FAD曲线，进入不合格区域，如图12所示。评估点曲线和FAD曲线的交点为失效判定的临界状态点，在上文计算得到的外载荷水平和初始裂纹组合（a0=4.5 mm，c0=22.5 mm）情况下，此临界点对应的临界裂纹尺寸为a=12.84 mm，2c=147.28 mm。

同时，从图13中可以看到，当初始裂纹深度和长度均较大时，最终裂纹深度值较大。原因为：当初始裂纹深度a0和长度c0的取值较大时，裂纹深度方向的扩展速率较大，故当循环次数相同时，最终裂纹深度值较大。初始裂纹的尺寸大小对裂纹扩展影响显著，合理地确定初始裂纹尺寸是分析裂纹扩展非常关键的一步。同时，当初始裂纹尺寸组合相同时，完成相同的载荷循环后，表面裂纹缺陷的最终裂纹深度值比埋藏裂纹缺陷对应的值要大，可见表面裂纹危害性比埋藏裂纹危害性更大，表面裂纹尖锐的裂纹尖端会引起应力集中，促使裂纹快速扩展造成严重事故。因此，为了科学合理地制定缺陷高强度厚钢板的检维修策略，对表面裂纹缺陷进行安全寿命评估是十分重要的。

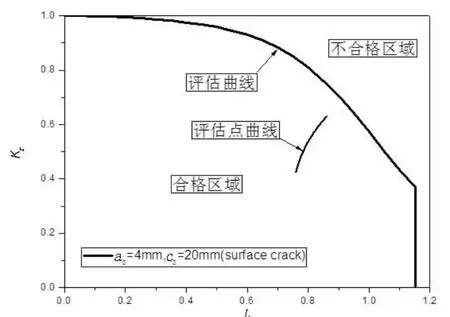
图10 表面裂纹失效评估图（a0=4 mm）Fig.10 FAD of surface crack

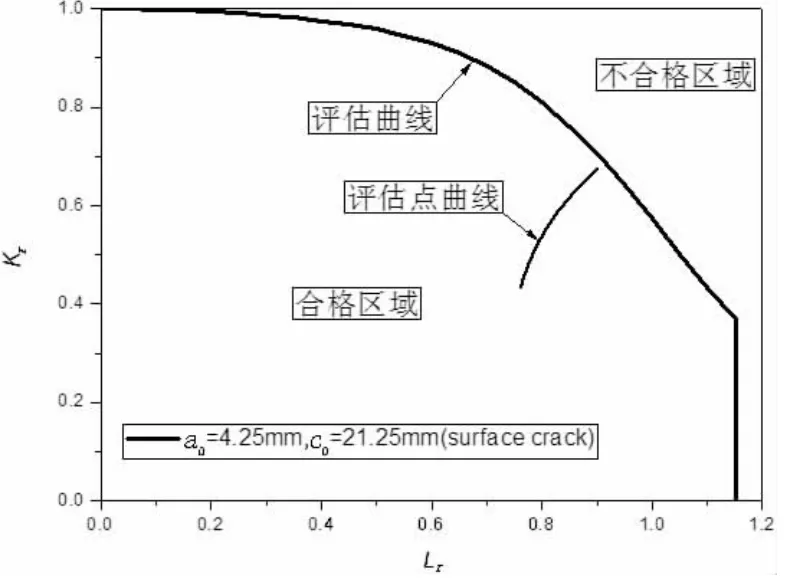
图11 表面裂纹失效评估图（a0=4.25 mm）Fig.11 FAD of surface crack

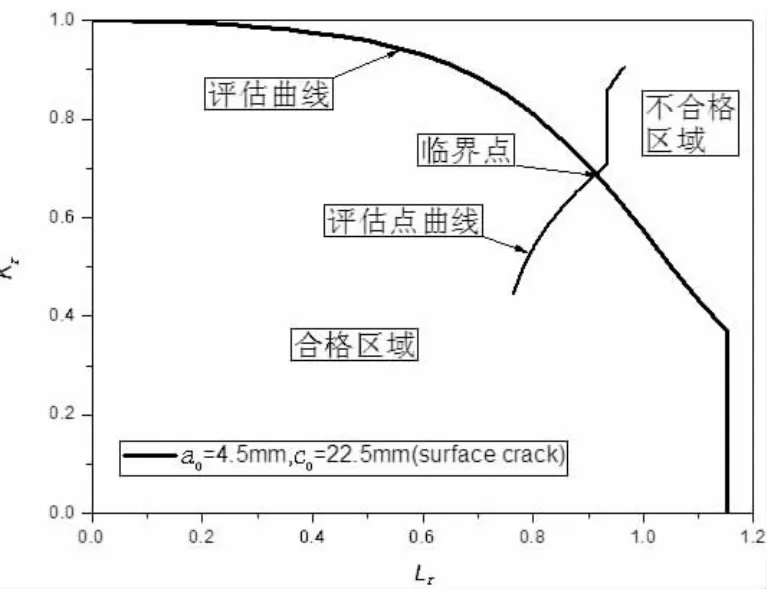
图12 表面裂纹失效评估图（a0=4.5 m)Fig.12 FAD of surface crack

图13 裂纹深度随循环次数的变化Fig.13 Variation of crack depth during cycles

5 结 论

根据裂纹扩展率单一曲线模型预报裂纹在船舶所受的波浪载荷作用下的扩展，并根据不同疲劳寿命下得到的裂纹尺寸用失效评估图技术进行安全性评估。分别对某大型集装箱船上甲板焊接接头上的表面裂纹和埋藏裂纹缺陷在复杂载荷作用下的疲劳寿命进行了评估，得到了以下结论：

（1）初始裂纹尺寸对裂纹扩展行为影响明显，高强度钢甲板安全寿命评估中确定合理的初始裂纹尺寸非常重要，在没有检测数据的情况下，可参照Yoichi等推荐的厚钢板初始缺陷裂纹的深长比来确定初始裂纹尺寸。

（2）当初始裂纹尺寸a0、c0和外载荷条件均相同时，表面疲劳裂纹对结构的危害性比内部的埋藏裂纹危害性更大。

（3）本文采用等效应力法将应力范围服从两参数Weibull分布的随机载荷转换为恒幅载荷谱，使计算得到较大的简化。但要注意这种简化对小裂纹不适用。

[1]李兆锋,江 楠.基于失效分析图对含缺陷压力容器的安全评定[J].化工设备与管道,2009,46(6):5-9.

[2]罗金恒,赵新伟,熊庆人,等.缺陷管道疲劳寿命预测新模型及试验验证[J].石油机械,2005,33(2):5-7.

[3]金伟良,付 勇,赵冬岩,等.具有裂纹损伤的海底管道断裂及疲劳评估[J].海洋工程,2005,23(3):7-16.

[4]张 立,金伟良.海洋平台结构疲劳损伤与寿命预测方法[J].浙江大学学报,2002,36(2):138-142.

[5]张丽娜,孙 姝,张富刚.在随机载荷作用下用断裂力学法估算潜艇耐压壳体的疲劳寿命和裂纹尺寸[J].舰船科学技术,2006,28(1):27-31.

[6]冯国庆,任慧龙,李 辉.实用船舶结构疲劳评估方法摘要[J].舰船科学技术,2009,31(1):23-28.

[7]Huang X P,Moan T.Improved modeling of the effect of R-ratio on crack growth rate[J].Int.J Fatigue,2007,29:591-602.[8]Huang X P.Fatigue crack growth rate recommended in BS7910 and an unique crack growth rate curve under different load ratios[C]//ASME PVP 2007/CREEP 8 Conference July 22-26,2007.San Antonio,Texas,USA,2007.

[9]Huang X P,Moan T,Cui W C.An engineering model of fatigue crack growth under variable amplitude loading[J].Int.J Fatigue,2008,30:2-10.

[10]Huang X P,Moan T,Cui W C.A unique crack growth rate curve method for fatigue life prediction of steel structures[J].Ships and Offshore Structures,2009,4(2):165-173.

[11]BS7910.Guide on methods for assessing the acceptability of flaws in metallic structures[M].British Standard Institution,2005.

[12]DNV.Fatigue assessment of ship structures[S].HØvik:Det Norske Veritas Classification Notes No.30.7,January 2001.

[13]冯国庆.船舶结构疲劳强度评估方法研究[D].哈尔滨:哈尔滨工程大学,2006.

[14]中国船级社.船体结构疲劳强度指南[M].北京:人民交通出版社,2001.

[15]陈传尧.疲劳与断裂[M].武汉:华中科技大学出版社,2001.

[16]Newman J C,Raju I S.Analysis of surface cracks in a finite plate under tension or bending loads[R].NASA TP-1579,1979.

[17]黄小平,贾贵磊,崔维成,等.海洋钢结构疲劳裂纹扩展预报单一扩展率曲线模型[J].船舶力学,2011,15(1-2):118-125.Huang Xiaoping,Jia Guilei,et al.Unique crack growth rate curve model for fatigue life prediction of marine steel structures[J].Journal of Ship Mechanics,2011,15(1-2):118-125.

[18]张 毅,黄小平,崔维成,卞如冈,等.对接接头焊趾应力集中有限元分析[J].船舶力学,2004,8(5):91-99.Zhang Yi,Huang Xiaoping,et al.Finite element analysis of contact on stress concentration at weld toe of butt-welded joints[J].Journal of Ship Mechanics,2004,8(5):91-99.

[19]中国船级社.材料与焊接规范[M].北京:人民交通出版社,2009.

[20]中国船级社.集装箱船结构强度直接计算指南[M].北京:人民交通出版社,2005.

[21]冯国庆,任慧龙.船舶结构疲劳评估的设计波法[J].哈尔滨工程大学学报,2005,26(4):430-434.

[22]Yoichi Sumi,Hiroshi Yajima,Masahiro Toyosada,et al.Overview of Japanese joint research project on safety-related issue of extremely thick steel plate applied to large container ships[C]//11th International Symposium on Practical Design of Ships and Other Floating Structures.Rio de Janeiro,R J,Brazil,2010.

Security life assessment of crack flaws in high tensile steel deck of large container ships

ZHANG Ding1,2,HUANG Xiao-ping1,DING Shi-feng3,HONG Ying3,XU Bo-wen3
(1 State Key Lab of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2 Marine Design&Research Institute of China,Shanghai 200011,China;3 Shanghai Rules&Research Institute,CCS,Shanghai 200135,China)

The fatigue loading is obtained based on the classification society rules and Weibull long-term checking stress range distribution.Equivalent stress method is used to transform random loading spectrum into constant loading spectrum.A procedure which consists of FAD technology and crack growth life prediction method is used to assess the security life of high tensile thick steel plates under complex loading conditions.Fatigue life of a surface crack and an embedded crack located at butt welded joint in the upper deck of a large container ship under complex loading conditions,considering the effect of welded residual stress,are assessed respectively.It is concluded that the initial size of crack has significant effect on crack growth behavior,and the harmfulness of surface crack on structural security is more serious than that of embedded crack in conditions of the same initial crack size and applied load.

high tensile thick steel plates;FAD(failure assessment diagram)technology;crack flaws;unique curve model;stress range;life assessment

黄小平（1963-），男，博士，上海交通大学教授。

U661.4

A

10.3969/j.issn.1007-7294.2014.05.008

1007-7294（2014）05-0540-10

2013-06-20

海洋工程国家重点实验室基金项目（GKZD010053-17）

张 鼎（1986-），男，上海交通大学硕士研究生，E-mail：zhangding@sjtu.edu.cn；