考虑初始形状影响的耐压球壳临界载荷简化计算公式

王 丹，万正权

（中国船舶科学研究中心，江苏 无锡 214082）

考虑初始形状影响的耐压球壳临界载荷简化计算公式

王 丹，万正权

（中国船舶科学研究中心，江苏 无锡 214082）

文章研究了在载人深潜器结构中承受高压、保障潜员安全的耐压球壳。文中通过对经典理论公式的分析和合理假设，引入几何修正系数k细化了球壳临界载荷计算表达式，该几何修正系数体现了球壳本身的初始形状，如初挠度、局部不圆度及板厚减薄等因素对其的影响。并通过回归分析得到计算数据与试验值吻合较好。同时，运用该公式对钛合金球壳临界载荷进行预报，同样有较高精度。

耐压球壳；临界载荷；载人潜水器；初挠度

1 引 言

球壳是深潜装备、航天航空、压力容器及核工业等领域常用的一种结构形式。这与球壳自身具备的物理特性有着密切的关系。与相同质量的其他复杂结构相比较，球壳具有容重比高的特点，只要布置合理就能够最大可能利用空间来承载；理想球壳的外表面受力均匀，在周向和径向的应力值相同，计算时只需关注膜应力数值即可控制设计参数；因其结构简单，在理论计算或数值模拟过程中选择的参数较少，变量仅剩厚度与半径。无论是深潜还是航天航空领域，选择球形结构作为载人舱都是比较适当。

球形载人舱肩负保障水下潜员安全、提供生命保障及作业条件方面的重任，球壳一旦发生失稳、破坏，后果将不堪设想。一直以来，球壳的安全性受到科研人员的广泛关注，各国科研人员对各种材料制成的球壳结构进行了大量的理论与试验研究，取得了丰硕的科研成果。而大多数科研是针对球壳的安全性进行的，如将球壳的安全性参数化，可用极限承载能力来衡量，而承载能力一般可以用强度和稳定性这两个特征来表示。随着科学技术的发展，材料学、晶像学在微观和宏观领域的研究，用于加工球壳的材料其本身强度均已达到深潜要求。然而，球壳成形的过程与许多不利因素有着紧密的关联，如材料的非线性变形、壳体与理想形状之间的初始偏差（初挠度）、板材滚轧减薄、焊接残余应力及其他工艺内应力等。这些因素在一定程度上都会影响到球壳的稳定性，它们的存在会使球壳损失一定的承载能力。

到目前为止，我国科研人员对球壳问题进行了长期不懈的研究，如罗培林[1]从实际工程使用中球壳的欧拉应力一般高于材料的屈服极限出发，应用两个经验常数来反映生产工艺过程对球壳承载能力的影响；在文献[2]中，作者根据梁柱失效原理，用极限应力函数来分析球壳的稳定性，获得较好的计算结果；刘涛[3]通过对材料非弹性模量的数据拟合分析，用直线拟合切线弹性模量，获得高精度耐压球壳失稳临界压力计算公式；陆蓓、刘涛、崔维成[4]通过有限元分析方法，提出合理的有限元分析模型并研究了初挠度的影响，给出了完善的耐压球壳极限强度与经典值的比值曲线以及初挠度效应曲线；俞铭华，王自力等[5]对潜水器耐压球壳结构研究进展进行了综述，并利用有限元对不同深度潜水器进行分析[6]，获得初始缺陷对耐压球壳承载能力的影响曲线；潘彬彬，崔维成[7]对深潜器载人球壳各国船级社规范设计公式进行了比较，指出公式计算的球壳厚度大多偏厚，需要制定统一的球壳设计公式；王丹，邱昌贤等[8]通过球壳模型试验及有限元数值模拟与泰勒水池公式、俄罗斯公式计算结果进行比较，分析初挠度对球壳的影响，提出这两种公式计算结果较为保守，有必要对其修正系数进行调整。

由前述研究可以看出稳定性问题求解大多通过理论计算和有限元分析来研究，而最有效的检验方法是进行模型试验，通过模型试验可以获得球壳实际失稳压力、失稳形态以及临界应力，有助于对修正系数进行调整，得到更精准的计算公式。本文从球壳的经典理论公式与经验公式着手分析，简化了球壳临界载荷计算公式，并利用模型试验结果进行回归分析，验证几何修正系数的临界载荷计算公式。

2 球壳的临界载荷计算

2.1 理想球壳理论临界载荷

在进行球壳极限承载能力的理论分析时一般会做基本假定，假设球壳材料无强化，具有基本的拉伸曲线图；初挠度形状为圆形，失稳形状与初挠度形状相同，可以通过求解轴对称问题来解决初挠度对结构承载能力的影响问题。

在实际分析方法中，由理想材料制成的具有正确形状的球壳理论临界载荷一般采用著名的崔林（Zoelly）关系式表示，即

其中：v为泊松比；E为弹性模量，MPa；R为球壳中面半径，mm；t为壳板平均板厚，mm；对于钢制球壳，其泊松比v=0.3，公式（1）可以表示为：

2.2 非理想球壳理论临界载荷

对非理想球壳进行分析时，需要考虑球壳的加工工艺、壳板真实厚度与额定厚度之间的偏差、球壳局部半径变化、真实球壳与理想球壳之间的偏差、材料性能、焊接残余应力等因素。厚度、半径等参数均可通过测量工具获得较为精确的数值，一般选择初挠度进行理论分析。球壳表面产生的初挠度对球壳本身产生附加弯曲作用，随着压力的不断增加，附加弯曲的作用也逐渐增强，引起塑性变形的力与弯矩也会随之增大。当球壳壳板不能抵抗初挠度引起的附加力和力矩时，就会发生失稳。因此，要获得真实的非理想球壳理论临界载荷就需要对理想球壳理论临界载荷进行修正。

Paliy教授在1991年就发表了关于壳体承载能力的文章[9]，其中带有修正系数的公式如下：

将（2）式代入（3）式中得到相应的理论临界应力关系式为

该公式已经应用在俄罗斯载人潜水器及深潜装备的分类和建造规范之中[10]。其中，α取值为：柱壳取0.95，球壳取1.2。β系数与很多不利影响有关，主要考虑了材料的机械性能、初挠度、焊接内应力及其他工艺内应力等。

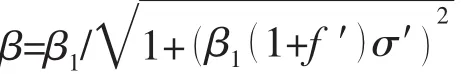
这里，β1=1/（1+（2.8+f ′）f2/3），f′为相对初挠度，f′=f/t，f为球壳偏离理想形状的最大初挠度；σ′为相对应力，σ′=σ/σs，σ 为临界载荷情况下对应的临界应力。

将α取值代入（5）式中并结合（2）式得到

2.3 带几何修正系数k的临界载荷计算公式

由（4）式和（7）式可以看出，两种情况下的理论临界应力比值中隐藏了修正系数β，则实际情况下的非理想球壳的承载能力关系式（6）可以变换为：

此时，利用（6）式，实际临界载荷情况下的临界应力可以写作：

如何能将球壳承载能力计算公式继续细化，不仅能直观地看出球壳半径与壳板厚度之间的关系，还能更加准确地计算出球壳的承载能力，这需要进行合理假设。引入材料屈服极限σs，假设其与σ之间的关系为

将（3）式和（9）式代入（8）式可以得到：

其中：k为几何修正系数，与球壳的厚度和半径变化量以及初挠度值有着密切的关系。将厚度和半径变化量的影响记作kt、kr，其值可以通过测量得到真实球壳的半径和板厚，并用（11）式和（12）式；将初挠度在临界弧长内的变化量的影响记作kf，kf=（1- fmax′ ），fmax′是最大相对初挠度，fmax′=fmax/t ，fmax为球壳实测最大初挠度值，有正负之分，负值表示凹陷，正值表示凸起，一般情况下认为最危险的状态是凹陷，在（12）式中fmax只取最大凹陷值。

kt、kr按照下式进行计算：

其中：tc为壳板平均厚度，通过初始形状测量获得，这样可以获得带有几何修正系数的球壳临界载荷计算公式：

3 球壳模型临界载荷试验值与计算值的比较

3.1 球壳的静水外压试验

中国船舶科学研究中心水下工程结构试验室针对2个（Q1-Q2）参数（直径、厚度、材料）相同，3个参数不同的球壳（Q3-Q5）进行初始形状测量，得到其初挠度值、局部凹凸度和壳板平均厚度等，之后对这些球壳分别进行了静水外压试验。

Q1-Q2模型直径较小，为半球焊接，最大相对初挠度值小于0.15，失稳压力较高；Q3-Q4模型直径较大，为瓣片式焊接（赤道面无对接焊缝），焊缝较多，最大相对初挠度达到0.43，失稳压力偏低；Q5模型直径较大，亦瓣片式焊接（赤道面有对接焊缝），焊缝与焊缝错开对接，最大相对初挠度仅0.15，在20 MPa静水外压情况下未发生失稳。球壳模型相关参数及失稳压力[11-13]列入表1，模型失稳后形状见图1和图2。

表1 球壳模型主要参数及失稳压力Tab.1 Main parameters and buckling loads of the spherical hull models

图1 Q1、Q2失稳形态Fig.1 The buckling shapes of Q1 and Q2

图2 Q3、Q4失稳形态Fig.2 The buckling shapes of Q3 and Q4

3.2 计算值与试验值的比较

应用本文给出的计算公式，根据5个球壳模型的实际测量数据计算临界载荷。将计算值与试验值进行比较，表2中列出了临界载荷计算值与试验值之间的偏差。

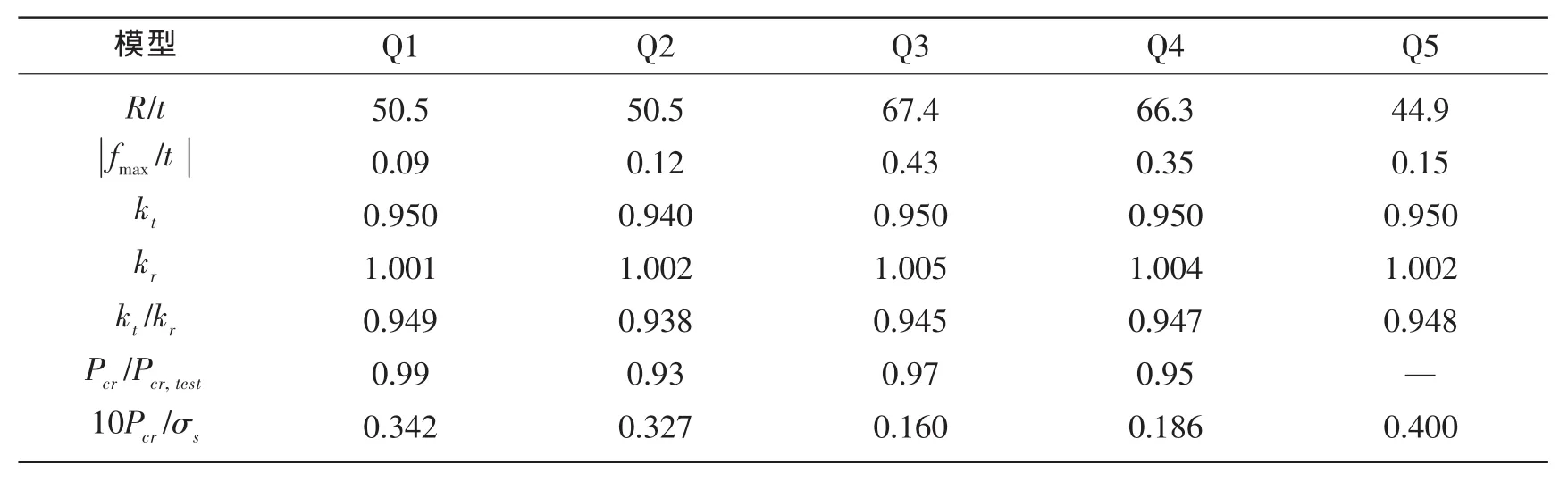
表2 利用本文给出方法对球壳模型临界载荷的计算Tab.2 Calculation of the critical loads for spherical hull models by the present method

图3是计算数据与试验值的趋势线。分析了在k值一定的情况下，最大相对初挠度与临界载荷之间的关系。利用回归分析对试验结果与计算结果进行比对，其相关系数达到99%以上。

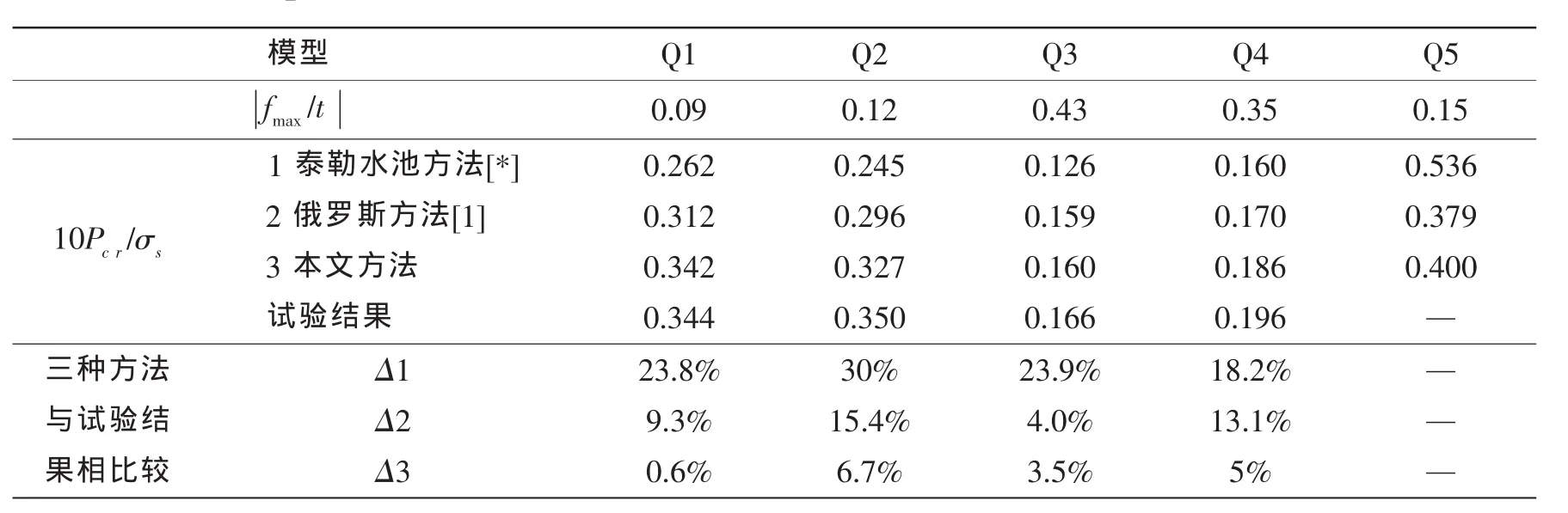
表3 三种方法计算结果与试验结果的比较Tab.3 Comparison between calculation results of the three methods and test results

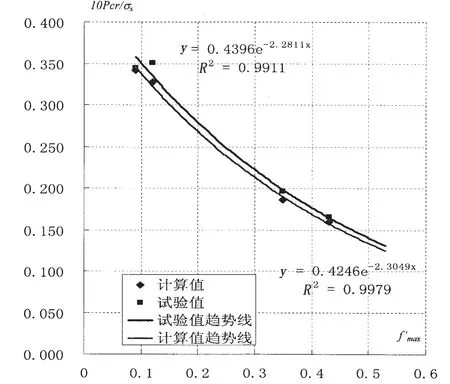
图3 本文方法计算值与试验值趋势线Fig.3 Calculation and test values trend lines

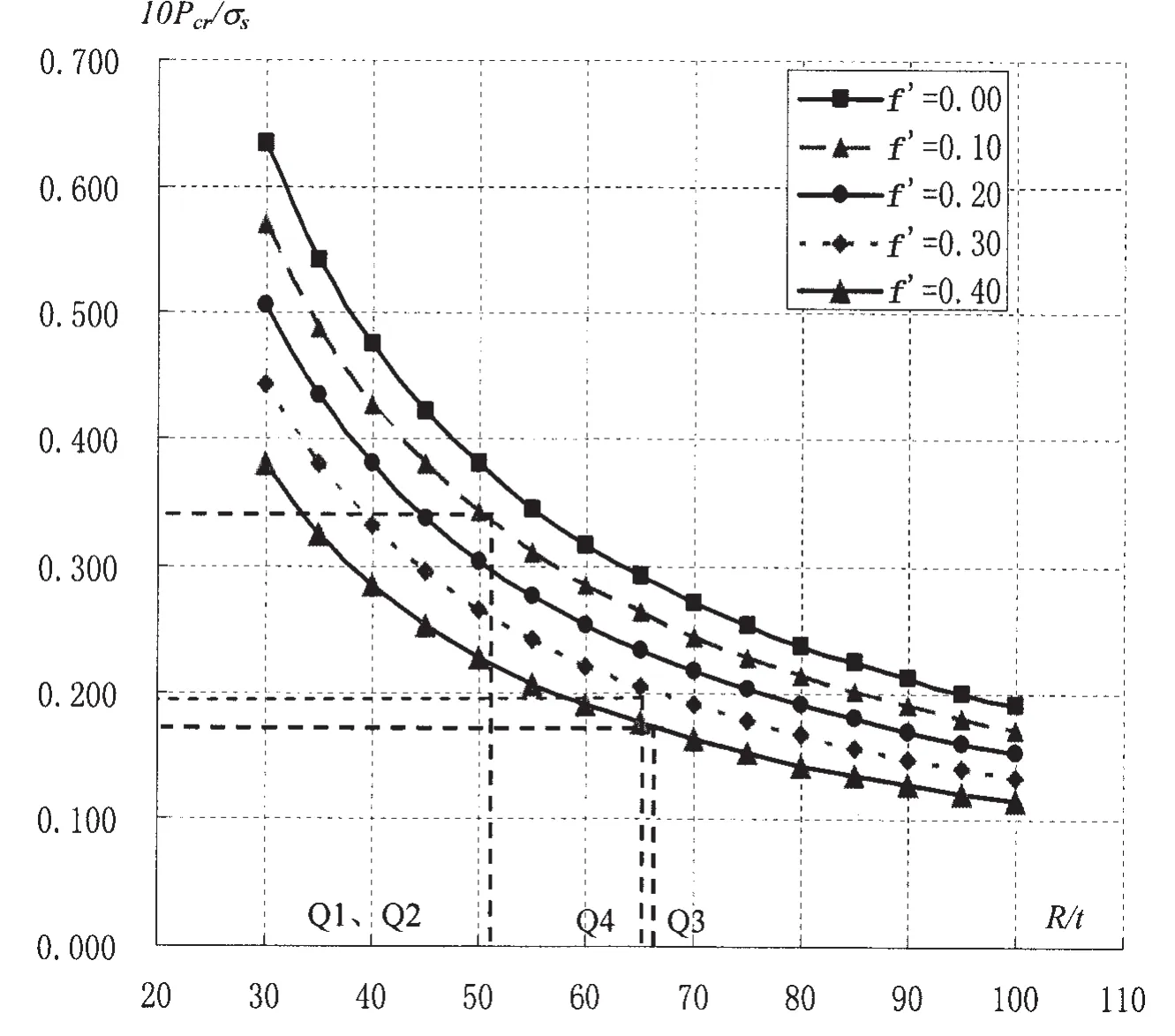
图4 当kt/kr=0.95时的临界载荷曲线Fig.4 Critical load curves for kt/kr=0.95

本文提供的计算方法与试验值之间的偏差较小，最大偏差为6.7%；用俄罗斯方法的最大偏差为15.4%，而用泰勒水池方法的偏差为30%，通过算例比较，本文方法更接近实际情况。

图4中以5个球壳模型为例，给出利用本文所给计算公式计算得到当kt/kr=0.95时的临界载荷曲线。可以看出在薄壳范围内，球壳的临界载荷随着半径厚度比的增加而减小；在相同R/t的情况下，临界载荷随着初挠度的增加而降低。

4 应用本方法对钛合金耐压球壳的临界压力进行计算

根据钛合金球耐压球壳模型的主要参数，运用本文方法进行临界载荷预报，与试验值对比结果见表4。

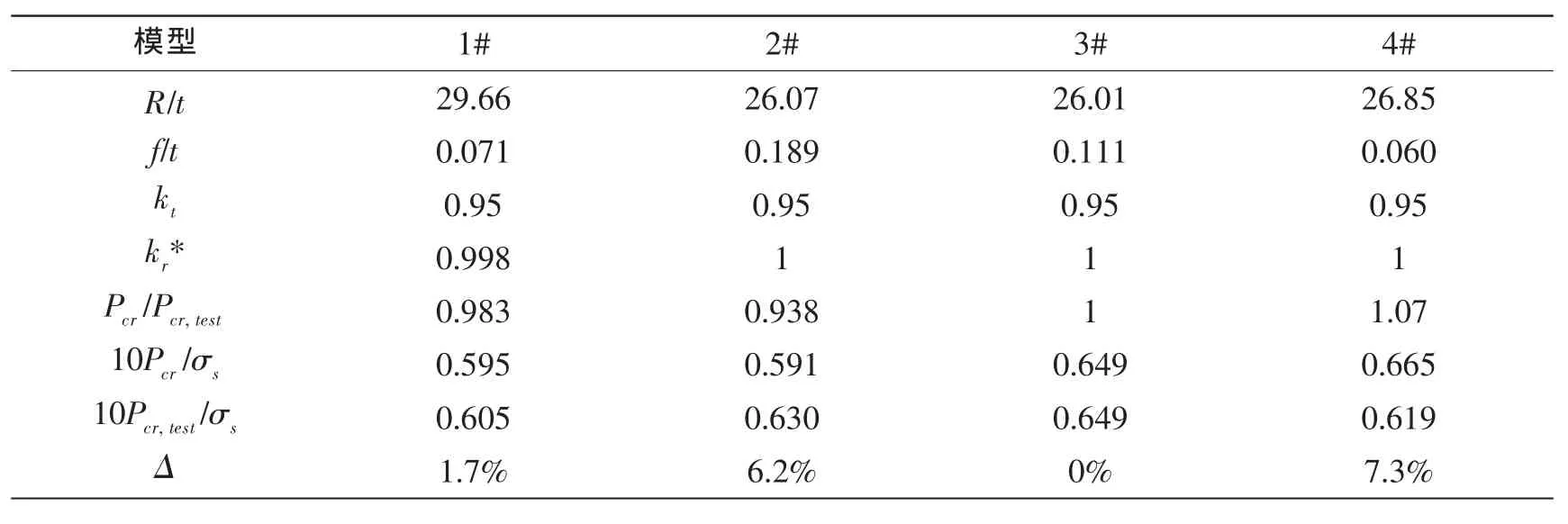
表4 钛合金球壳模型主要参数及临界载荷计算结果Tab.4 Main parameters and calculation results of critical loads for titanium alloy spherical hull models

可以看出运用本文方法预报的钛合金球壳模型临界载荷与其静水外压试验值比较吻合，最大偏差不超过7.3%。该方法可以运用到钛合金球壳临界载荷的预报中。

5 结 论

本文未考虑焊接残余应力及其他装配内应力对球壳临界载荷的影响，下面给出根据本文简化公式计算及分析得到的结果：

（1）简化公式需要得知精确的初始形状测量数据，如板厚、半径、初挠度或不圆度等才能得到更接近实际情况的计算结果；当球壳为精加工模型时（球壳的半径变化不大，且初始缺陷较小），影响承载能力的因素主要是壳板厚度；

（2）当球壳的半径、厚度变化量的关系kr/kt变化不大时，初挠度对球壳的影响更加显著；当初挠度值增加5%左右，临界载荷会随之降低，泰勒水池方法降低约11%[8]，俄罗斯方法降低约5%，本文方法随初挠度的增加表现出非线性变化，初挠度每增加5%，临界载荷降低量从5%～7%逐渐增加；

（3）在薄壳范围内（R/t＞20），临界载荷随着R/t的增大而减小，本文方法适用于钛合金制造的球壳结构临界载荷计算；

（4）本文方法预报的临界载荷与试验值的某些偏差超过5%，需要对简化计算公式进行进一步的修正，使得计算结果与试验值更加接近；

（5） 根据强度标准（σ≥0.85σs）的要求反推得出：k=kf·kt/kr≥0.85；此时，即从强度方面限制了球壳厚度、半径及初挠度的变化量参与求解球壳稳定性问题。

[1]罗培林.厚球壳的极限载荷-均匀压力-计算与模拟试验方法的改进,1976,手写稿.1994-2012 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net.[J/OL].

[2]罗培林.用极限分析方法分析梁柱和球壳的稳定性[J].哈尔滨工程大学学报,1981,2:21-50.

[3]刘 涛.大深度潜水器耐压壳体弹塑性稳定性简易计算方法[J].中国造船,2001,42(3):8-14.

[4]陆 蓓,刘 涛,崔维成.深海载人潜水器耐压球壳极限强度研究[J].船舶力学,2004,8(1):51-58.Lu Bei,Liu Tao,Cui Weicheng.Ultimate strength of pressure spherical hull in deep-sea manned submersibles[J],Journal of Ship Mechanics,2004,8(1):51-58.

[5]俞铭华,王自力,李良碧,王仁华.大深度载人潜水器耐压壳结构研究进展[J].华东船舶工业学院学报(自然科学版),2004,18(4):1-6.

[6]王自力,王仁华,俞铭华,李良碧.初始缺陷对不同深度载人潜水器耐压球壳极限承载能力的影响[J].中国造船.2007,48(2):45-50.

[7]潘彬彬,崔维成.深潜器载人球壳规范设计公式的比较[J].船舶力学,2011,15(3):276-285.Pan Binbin,Cui Weicheng.A comparison of different rules for the spherical pressure hull of deep manned submersibles[J].Journal of Ship Mechanics,2011,15(3):276-285.

[8]Wang Dan,Qiu Changxian,Wang Yongjun,Wan Zhengquan.Theoretical and experimental research of spherical pressure hull[C].船舶与海洋结构力学学术会议,2011:68-76.

[9]Paliy O M.Weight characteristics,reliability and operational safety of deep-sea submersible hulls[C]//International Symposium on Marine Structures(ISM’91),September 13-14,1991.Shanghai,China,1991:197-199.

[10]Правила классификации и постройки обитаемых[Z].подводных аппаратов и глубоководных водолазных комплексов[Z].1993.

[11]王 丹,杨华伟,王永军.超大潜深耐压球壳开孔模型试验[R].无锡:中国船舶科学研究中心科技报告10696,2010.

[12]王 丹,王永军.超大潜深耐压球壳无开孔模型试验[R].无锡:中国船舶科学研究中心科技报告10171,2010.

[13]王 丹,杨华伟,王永军.超大潜深耐压球壳模型理论与试验分析报告[R].无锡:中国船舶科学研究中心科技报告10351,2010.

Simplified calculation formula for critical load of spherical pressure shell considering the influence of initial shape

WANG Dan,WAN Zheng-quan
(China Ship Scientific Research Center,Wuxi,214082,China)

The spherical pressure shell main structure of manned submersible which is under great pressure and provides the security of human is researched.A new formula for calculating critical load of the spherical shell which bases on classic theory and considers the correction coefficient k is introduced.The influences of initial shape are shown,for example,initial deflections and out-of-roundness and thickness thinning in the manufactory technical,etc.The calculated data agree well with the experimental data by the regression analysis.The critical load of titanium spherical shell predicted by this formula is very precisely.

spherical pressure shell;critical load;manned submersible;initial deflections

U661.4

A

10.3969/j.issn.1007-7294.2014.05.010

1007-7294（2014）05-0557-08

2013-10-28

王 丹（1981-），女，中国船舶科学研究中心工程师，E-mail：wangdan21@hotmail.com；

万正权（1962-），男，研究员，博士生导师。

book=564,ebook=412