基于神经网络的传感器非线性误差校正方法

樊润洁，朱亚男

（西安铁路职业技术学院 陕西 西安 710014）

传感器作为测控系统的感知器件，在测控系统中占有举足轻重的地位。不同的测控系统对其使用的传感器要求虽不尽相同，但无一例外都要求保证传感器的测量准确度。由于传感器的输入与输出关系中存在非线性误差，该误差会导致传感器测量结果的准确性大幅降低。因此，研究传感器非线性校正方法以进一步提高传感器测量精度非常必要。

近年来，人工神经网络技术已成为一个研究的热点技术，人工神经网络（即神经网络）是一种模拟大脑神经的突触连接结构进行信息处理的数学模型，是对人脑的抽象、简化和模拟[1-2]。为了提高传感器精度，探索更加准确便捷的传感器非线性误差修正方法，本文采用神经网络技术来进行传感器的标定研究。

1 传感器非线性误差分析

不考虑环境及其他因素影响，仅考虑传感器非线性分析传感器误差。

传感器的非线性误差是指传感器的输出是输入的非线性函数，如式（1）所示：其中y应为传感器输出结果，k为传感器线性修正系数，x为传感器输入，β（x）为传感器输入-输出关系的非线性修正函数。

利用泰勒公式将式（1）展开，得到式（2）：其中，β（x0）是常量。

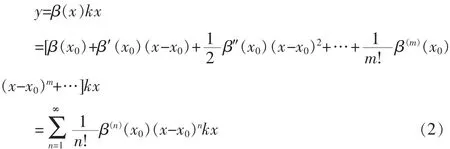
由式（2）可看出，由于非线性因素的存在，使得传感器输入-输出函数关系较为复杂，如不加以修正，会使测量结果产生较大误差，尤其在复合测量系统中，多个传感器的误差发生叠加会使得综合输出结果产生更大偏差。因此，在使用传感器之前，需对其进行非线性修正，即对传感器进行标定。

2 数据采集

文中以对磁质伸缩位移传感器的标定为例，目的是修正其非线性误差，使其精度达到测控系统要求。实验硬件采用精密数显高度尺获得实际位移值，采用装有A/D采样卡的工控机实现信号采集。

为抑制噪声信号的干扰，保证采样信号的准确性，采用移动平均滤波技术获得采样信号。具体过程是：将连续采样的信号瞬时值存储在一个长度为的数据列中，每次采样后用新的数据替换上述列中的数据，然后将该列中的数据加权平均作为采样电压值记录。

第 k（k≥N）次采样输出的采样电压值 xt（k）由式（3）计算：

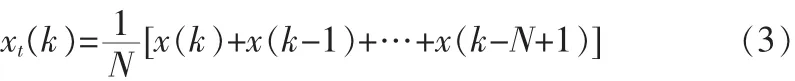
其中 x（i）为第 i次采样的信号瞬时值，N=800。式（3）的意义是将第k次连同前（N-1）次采样的信号瞬时值取其算术平均值作为采样电压值输出。

本次实验需进行重复性检验、标定以及标定结果的校准，故需采样3组数据。其中数据1和数据2为在相同位移处采样数据，用于重复性检验；数据3的用于校准需取不同于数据1、2采样点位移的位置采样。实验中每20 mm采样一个电压值。

在相同位移处重复做两次实验，实验1和实验2测得的采样电压—位移图如图1所示，横坐标表示采样电压值，纵坐标表示经换算得到的输出位移值，实验1与实验2的实验数据是在保证纵坐标位移值不变的情况下采样的两组不同电压值。

由图1可知，在相同位移点所做的两次实验的采样电压值差异很小，说明传感器重复性较好，这为标定实验的准确性提供了保证。

3 校正方法比较

对于相同的采样数据，分别采用最小二乘拟合、BP神经网络以及RBF神经网络三种方法得到标定位移值[3-5]，并利用实验3的校正数据进行检验，比较三种方法非线性补偿结果的优劣。

3.1 最小二乘法拟合

采用最小二乘法拟合时，首先需确定拟合多项式的次数，经多次实验，确定采用4次多项式拟合采样电压和实际位移值。以数据1中采样电压值为采样点X，实际位移为采样点函数值Y，拟合得到的4次多项式见式（4）：其中P（x）为对应采样电压值的拟合位移值。

采用式（4）输出的拟合位移值与实际采样位移值比较，从而得到拟合结果的准确度评判，并以校准实验3的数据代入式（4）得到校准拟合结果，这样就分别得到了采样点及校准点两组拟合误差，如图2所示。

由图2知，采样点最大误差的绝对值约为5.72丝；校准点最大误差的绝对值约为6.21丝。校准误差可作为最小二乘法拟合精度的判断标准。

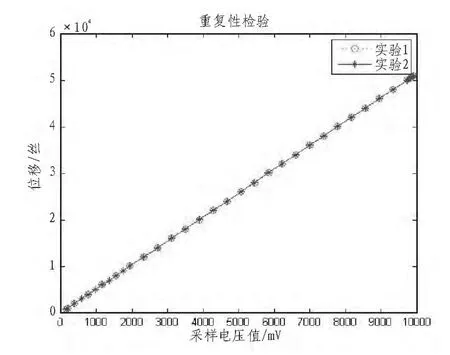
图1 重复性检验结果Fig.1 Repeatability of test results

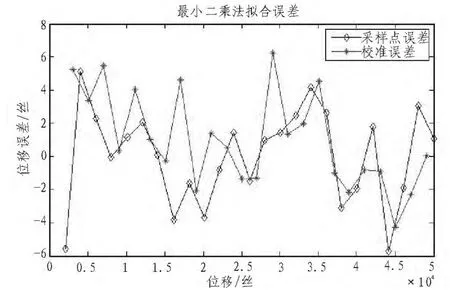
图2 最小二乘拟合误差Fig.2 Least-squares fitting error

3.2 BP神经网络标定

BP（Back Propagation）网络是目前应用最为广泛的神经网络模型，是一种单向传播的多层前馈网络。采用BP神经网络的方法对位移传感器进行非线性补偿。因为在本次实验中不考虑环境等其他因素对传感器输出的影响，故设计网络输入为数据1中采样电压X，输出为标定位移P，选择适当的参数建立网络。为了保证网络训练结果的准确度，需对网络输入与输出数据进行归一化处理，将归一化处理后的输入输出数据代入并训练网络，保存训练好后的网络，并记录网络计算输出的采样点拟合结果。为验证网络对非线性误差的修正效果，将校准实验3的数据代入网络使之计算输出校准拟合结果，将采样点拟合结果和校准拟合结果与实际位移值比较，同样可分别得到BP网络的采样点和校准点两组训练误差，如图3所示。

由图3知，采样点最大误差的绝对值约为10.21丝，校准点最大误差的绝对值约为10.97丝。校准点最大误差可作为BP网络拟合精度的判断标准。

3.3 RBF神经网络标定

图3 BP网络训练误差Fig.3 Training error of BPnetwork

径向基函数（Radial-Basis Function，RBF）神经网络（RBF网络）是一种典型的局部逼近网络模型。RBF网络通过隐层单元对输入数据矢量进行变换，将低维模式输入数据变换到高维空间中，使得低维空间内的线性不可分问题转换为高维空间内的线性可分。RBF网络已被证明能够逼近任意非线性函数，该网络自提出以来，就由于其具有的最佳全局逼近性能而备受关注。与其他类型的神经网络相比，RBF网络不仅具有较强的生理学基础，而且其结构简单，在学习速度、逼近性能等方面更具优势。

考虑到上述RBF网络优良的非线性逼近性能，采用RBF网络对该位移传感器进行非线性补偿。建立RBF网络一般需建立三个完全不同的层：即输入层、隐含层和输出层。第一层为输入层，输入层由源节点（即感知单元）构成；第二层为隐含层（也称隐层），隐层为径向基层，其节点数视具体问题不同而定；第三层为输出层，输出层提供网络对输入模式的响应。

RBF网络利用径向基函数作为隐层神经元的基构成其隐层空间，当径向基函数的中心确定后，从输入空间到隐层空间的映射关系就确定了。隐层空间到输出空间的映射则是线性的，即RBF网络的输出是由隐层神经元输出的线性加权和决定的。因此总体上讲，RBF网络实现了由输入空间到输出空间的非线性映射，具体而言，RBF网络从输入空间到隐层空间的变换是非线性的，而从隐层空间到输出空间的变换是线性的。

根据上述RBF网络结构及特点，构建用于该位移传感器非线性拟合的网络结构模型。同样在实验中不考虑环境等其他因素对传感器输出的影响，依然设计网络输入为数据1中采样电压X，输出为标定位移P（输入输出与BP网络相同）。网络结构如图3所示。

图4 非线性补偿的RBF网络结构Fig.4 RBF Network structure of nonlinear compensation

图4 中，φ为高斯径向基函数的一般形式，即：

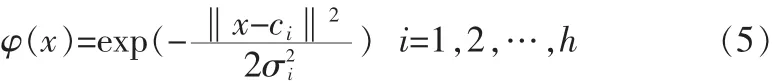
式5中，ci为径向基函数的中心；σi为扩展常数，决定了基函数的宽度；‖·‖为范数，通常取为欧几里得距离。

为保证网络输出精度，训练RBF网络所采用的输入输出数据均需进行数据归一化处理，把经归一化处理后的数据代入如图4所示的结构中以训练RBF网络。网络训练好后可用数据1中的采样电压输入得到一组采样的网络拟合位移值，为验证网络准确性，将校准实验数据3代入训练好后的网络验证，得到一组校准数据的网络拟合位移值，将采样拟合位移值和校准拟合唯一值与实际位移值比较，可以分别得到RBF网络非线性校准的采样点和校准点两组网络误差，如图5 所示[6-7]。

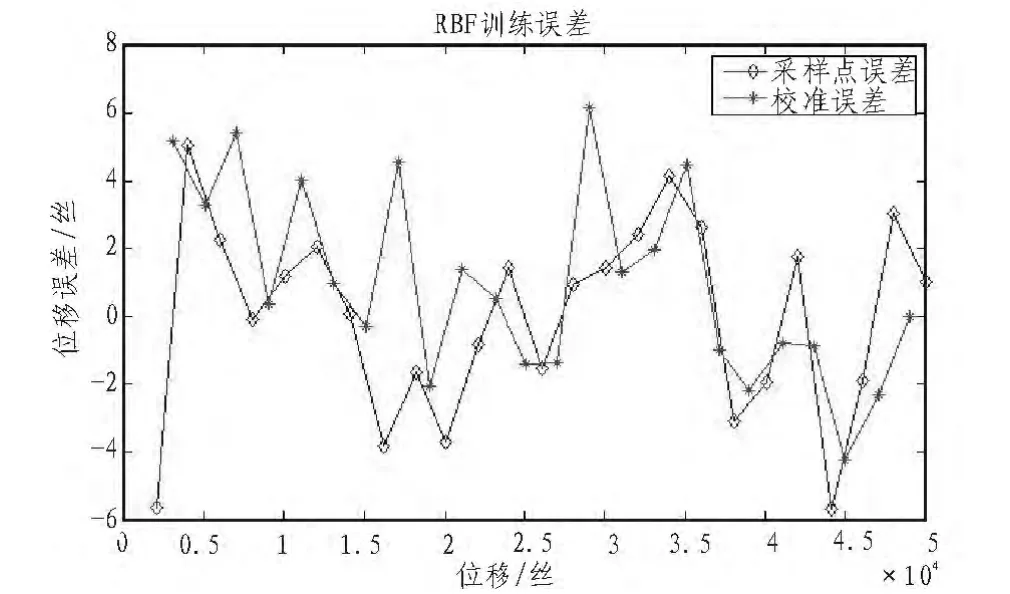
图5 RBF网络训练误差Fig.5 Training error of RBF Network

由图5知，采样点最大误差的绝对值约为5.71丝，校准点最大误差的绝对值约为6.17丝。同样可以采用校准点最大误差可作为RBF网络拟合精度的判断标准。

3.4 比较结果

将利用3种方法对该位移传感器进行非线性补偿的标定结果最大误差的绝对值汇总如表1所示。

表1 三种方法标定结果最大误差比较Tab.1 Calibration maximum error of three methods

由表1可知，对现有采样样本点来说，RBF网络训练结果非线性校正效果最好：相比较BP网络的输出误差，其校准点精度提高了约44%，极大地提高了传感器测量精度。相比最小二乘的拟合方法，虽然其校准点拟合精度提高不显著，但考虑到本次实验环境比较单纯，没有环境扰动因子，且传感器种类单一，仅为一种位移传感器，这种情况下传感器输入与输出函数关系更接近多项式函数，故在简单情况下最小二乘法也能体现良好的拟合性能。但是一旦传感器种类多样化或者环境因素复杂的情况下，最小二乘法的多项式函数就不再能提供较好的非线性补偿了，这种情况下采用RBF网络的补偿方法，可以逼近任意非线性函数，其非线性补偿优势更为显著。

4 结 论

文中为对位移传感器进行非线性补偿，分别采用了最小二乘拟合、BP神经网络[8]以及RBF网络三种方法进行标定，分析实验结果可发现，采用RBF网络进行非线性误差补偿效果最好。

虽然最小二乘拟合也具有较好的修正效果，但必需是以确定了合适的拟合次数为前提，当传感器类型不同时，为获得较好修正效果就需重新确定拟合次数。同时由于本实验传感器输出主要取决于其输入位移值，其他因素影响较小，传感器校准模型较简单，而当环境误差及其他影响因素较大时，传感器输入-输出函数复杂度将加剧，采用单一多项式拟合的方法将无法达到预期精度。

同时，BP网络由于其在网络建立和训练过程中，确定部分网络参数等并没有明确的理论指导，要确定最优的网络参数比较繁琐，且在逼近非线性函数的能力上RBF网络更具优势，因此其修正结果远不如RBF网络。

采用RBF网络的方法修正传感器非线性误差时，除具有较好的误差补偿效果外还具有以下两点优势：

1）当环境和其他因素影响加剧时，RBF网络依然可以达到较好的误差补偿效果；

2）在对多种不同类型的传感器进行标定时，RBF网络参数调整较为简单，使用更加方便，具有良好的鲁棒性。

[1]Simon Haykin．Neural networks expand SP’s horizons[J]．IEEE Signal Processing Magazine，1996，13（2）：24-49．

[2]Powell M J．Radial basis function for multivariate interpolation[R]．England：Cambridge University，1985．

[3]戴葵.神经网络实现技术[M].长沙：国防科技大学出版社，1998.

[4]高隽.人工神经网络原理及仿真实例[M].北京：机械工业出版社，2003.

[5]蔡煜东，姚林声.传感器非线性校正的人工神经网络方法[J].仪器仪表学报，1994，15（3）:299-302.CAI Yu-dong，YAO lin-sheng.Artificial neural network approach to nonlinear calibration for sensors[J].Chinese Journal of Scientific Instrument，1994，15（3）:299-302.

[6]刘卫国.MATLAB程序设计教程[M].北京：中国水利水电出版社，2005.

[7]魏巍.MATLAB控制工程工具箱技术手册[M].北京：国防工业出版社，2004.

[8]高原.基于BP神经网络的文本验证码破解[J].电子科技，2012（7）:37-42.GAOYuan.Text captcha crack based on BPneural network[J].Electronic Science and Technology，2012（7）:37-42.