直驱永磁风力发电机风能最优控制
2014-01-16李永东宋瑞瑞
李永东,宋瑞瑞
(1.江苏油田试采二厂 江苏 金湖 211600;2.河海大学 能源与电气学院,江苏 南京 210098)
风能作为清洁能源,越来越受到全球各国的关注,风力发电逐渐成为许多国家可持续发展战略的重要组成部分,根据全球风能理事会今年4月发布的全球风电市场发展报告,全球风电年新增总计达到44.8GW,比2011年增加了10%。全球风电总装机容量达到282.5 GW, 同比增长19%。预计全球在未来五年(2013- 2017)累计市场的平均增长率约在13.7%, 累计装机容量将实现翻番,达到536 GW。2009-2011年,中国保持年新增装机容量全球第一的位置,到2020年我国风电总装机容量将达到30 GW。因此,对于风力发电机中最大风能捕获控制成为了各国研究的焦点。
各国对基于双馈感应发电机(doublyfed induction gene rators, DFIG) 的风力机发电技术的研究很多, 目前已经发展成熟。然而对于直驱永磁同步风力发电机组(D-PMSG) 的研究则相对较少, 因其以效率高、寿命长、噪声小、发电机结构简单和维护工作量小等特点, 在风力发电领域受到了越来越多的重视,而且根据文献[1]的分析,直驱永磁发电机有望逐渐成为大型风力发电机组的主流,并首先会在对发电机组的可靠性和可维护性要求更高的海上风电场获得大规模的应用。
1 D-PMSG简介
永磁同步风力发电系统结构如图1所示 ,变桨距风轮机直接耦合永磁同步发电机,发电机输出由不可控整流后由电容支撑,再经逆变器将能量馈送给电网,本文主要针对风力发电机工作特性,寻找最佳风能捕获点。
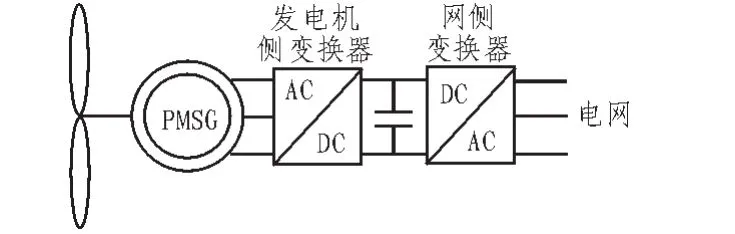
图1 D-PMSG系统Fig. 1 D-PMSG system
2 D-PMSG的数学模型
2.1 风力机模型
风力机的输出功率[2]:

ρ是空气密度,单位为kg/m3, R为风力机转子半径, β为风力机桨叶的桨距角,λ为叶尖速比, Cp(β,λ)为与桨距角和叶尖速比λ有关的功率系数,ωw为风力机转子转速,单位为rad/s, Vw为风速,单位m/s。
功率系数Cp定义为:
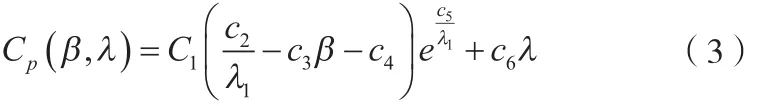
式中取值 C1~C6分别为 C1=0.22,C2=115,C3=0.4 ,C4=5 ,C5=21,C6=0.006 8,当桨距角 β一定时,Cp-λ的曲线为:

图 2 风机Cp-λ 曲线Fig. 2 Cp-λcurve of a wind turbine
图中,对应于任一桨距角,总有一个最佳 (λ,Cp) ,使得风能转化效率最高。
风力机的输出功率与气动转矩的关系:

综合(1)、(2)风力机气动转矩:

风力发电机组传动系统模型[3]:
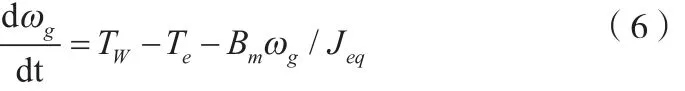
其中ωg为发电机转子转速,单位rad/s ,Te为电磁转矩,Bm为转动粘滞系数, Jeq为机组的等效转动惯量。
根据dq同步旋转坐标系下永磁同步电机的定子电压模型可得:

电磁转矩为:

其isd, isq分别为永磁同步发电机定子电流的d轴和q轴分量, usd, usq分别为定子电压的d轴和q轴分量,Ld,Lq分别为发电机的d轴和q轴电感,对于永磁风力发电力,Ld=Lq, Rs为定子电阻, ψf为永磁体磁链, ωe为电角速度。
2.2 最大风能捕获原理
由图2可知,风机功率因素在桨距角等于0°时(即最优桨距角)可以取得最大值,因此,在研究最大风能捕获最优控制时,不考虑桨距角的动态变化,并将其固定在最优桨距角状态。当永磁同步风力发电机机组被选定后,综合公式(1)、(2)、(3)可以从图3得到,在定桨距下风力机在不同风速Vw下轴上输出的功率Pw与转速ωw的关系。可以看出,风速 Vw一定时,转速ωw不同会使风力机输出功率不同,也即在特定风速下,总有一个的最佳转速ωwopt使风力机运行于此转速下,会从而捕捉最大风能,输出最大功率。

图3 风机输出功率特性曲线Fig. 3 Power characteristics of a wind turbine
3 粒子群算法
3.1 基本概念
粒子群算法 (Particle Swarm Optimization,PSO)由 Kennedy和Eberhart于1995 年首先提出的一种进化算法,通过模拟鸟群飞行觅食行为中个体之间的协作来寻找最优解的进化计算技术; 是一种基于个体改进、种群协作与竞争机制的进化计算方法,具有理论简单、易于编码实现和计算消耗低的特点。
在PSO中,每个优化问题的解都是搜索空间中的一只鸟。称之为“粒子”(Particle)。所有的粒子都有一个由被优化的函数决定的适应值,每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。
算法初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解,这个解叫做个体极值Pid。另一个极值是整个种群目前找到的最优解Pgd。这个极值是全局极值。
每个粒子的速度v和位置更新公式如下[4]:

式中,vid,t和 xid,t+1分别为第i个粒子的第d维度,在第t+1迭代中飞行速度和所在位置;Pid,t为第i个粒子的第d维度在t+1次迭代中个体最佳位置;Pgd为迭代过程中产生的全局最佳的粒子位置;r1、r2为[0-1]的随机数; c1、c2为权重系数;ω为惯性因子。
文中采用线性惯性因子,达到初期全局探测和后期局部深入的寻优效果,惯性因子变化如下:

其中, ωmax和ωmin表示最大和最小惯性因子,一般分别取0.9和0.4, ωt为当前惯性因子, t为当前迭代次数, T为最大迭代次数。算法的流程如图4所示。

图4 PSO流程图Fig. 4 Flow diagram of PSO
3.2 算例分析
各参数取值如下:

表1 风机参数Tab.1 Time of Different computing algorithms
本文适应度函数为发电机电磁率:

利用MATLAB语言编码,粒子群参数为:粒子个数20;最大迭代次数50。假设给定风速为12 m/s时,仿真寻找到的最大风能功率点如中的红色点,寻优迭代次数如图5图6所示:

图5 最大功率点Fig. 5 Maximum Power Point
此时的最大功率为1.12MW ,它占风机额定功率的74.5%,与风机在风速12 m/s的理论最大功率吻合,证明粒子群算法很好的找到了风速与转速参数匹配下的最大功率点。

图6 迭代次数Fig. 6 Mumber of iterations
4 结 论
文中运用了粒子群优化算法解决了永磁同步发电机最大风能的捕获问题,通过搭建的MATLAB仿真模型准确找到了获得最大风能的最佳转速,从而验了理论的可行性,因此,该方法是提高风能捕获的有效途径之一。
[1] 程明,张运乾,张建忠.风力发电机发展现状及研究进展[J].电力科学与技术学报, 2009, 24(3): 2-9.CHENG Ming, ZHANG Yun dry,ZHANG Jian-zhong.Development of wind turbines and research progress [J].Electric Power Science and Technology,2009,24(3):2-9.
[2] 张梅.直驱永磁同步风电机组建模及其控制系统仿真研究[D].西安:西安理工大学,2008.
[3] 尹明,李庚银,张建成等.直驱式永磁同步风力发电机组建模及其控制策略[J].电网技术,2007, 31(15): 61-65.YING Ming, LI Geng-yin,ZHANG Jian-cheng,etc.direct-drive permanent magnet synchronous wind turbine modeling and control strategy [J].Power System Technology,2007,31(15):61-65.
[4] KennedyJ, Eberhart R.Particle swarm optimization[C]//Neural Networks,1995.Proceedings,IEEE International Conference on.IEEE, 1995(4):1942-1948.
[5] 谢运祥, 卢柱强. 基于MATLAB/Simulink的永磁同步电机直接转矩控制仿真建模[J].华南理工大学学报: 自然科学版,2004,32(1):19-23.XIE yun-xiang,LU Zhu-jiang.based on MATLAB / Simulink permanent magnet synchronous motor direct torque control simulation modeling [J].South China University of Technology:Natural Science Edition, 2004, 32 (1):19-23.
[6] 薛定宇. 控制系统仿真与计算机辅助设计[M].北京: 机械工业出版社,2005.
