旋转封闭薄壁球壳辐射噪声的多极展开方法

侯明明，吴九汇，姜 宁

（1.西安交通大学机械工程学院，710049，西安；2.南通职业大学机械工程学院，226007，江苏南通）

旋转机械工作时产生的噪声主要包括机械结构噪声和气动噪声两大部分。机械在正常运转时，气动噪声占主要成分，也是比较难以控制的。由于气动噪声产生的机理十分复杂，目前还缺乏能完全驾驭复杂流动过程噪声产生机理及其分布的成熟理论和系统设计体系。因此，旋转机械气动噪声产生及分布机理的研究具有重要意义。

20世纪中后期，“声比拟”理论的提出及应用使得气动噪声理论研究取得突破性进展［1］。1952年英国科学家Lighthill运用声类比法得到了著名的Lighthill方程［2-3］，这成为研究气动声学问题的基本方程。1955年Curle采用Kirchhoff积分方法将Lighthill的理论推广到考虑静止固体边界的影响的理论［4］。1969年 Fowcs Williams和 Hawkings应用广义Green函数法将Curle的结果扩展到考虑运动固体边界对流体发声的影响，得到了著名的FWH方程［5］，FW-H方程被认为是迄今为止Lighthill声学类比法最一般的表达形式。除“声比拟”方法外，20世纪60年代，Powell和Howe等研究了声波和湍流的相互作用问题［6-9］。研究表明，声波的产生同流体中的旋涡具有密切的关系，从而提出了涡声理论，该理论较“声比拟”方法能更明晰地从物理意义的角度解释声波的产生以及声波与涡之间的能量关系。另外，Lighthill详细研究了点源作匀速直线运动时产生的声场，得到了辐射声场在远场的结果［1］。Lowson详尽研究了点声源在任意运动情形下产生的声场，并得到了该情形下点声源在远场的声压解［10］。

另一个经典的声学公式是Kirchhoff方程，该方程是假设在声源周围有一个流动状况已知的假想面，然后通过积分来求解线性声学问题。为了确保在假想面外线性声场占据主导地位，这个面所在的位置必须距离声源足够远［11］。1882年Kirchhoff公式被首次提出，1930年Morgans用格林函数法推导出了运动声源面的Kirchhoff公式，1988年Farassat和Myers运用广义函数理论推导出了更一般形式的 Kirchhoff公式［12］。

对于叶片式旋转机械来说，流激振动引起的外部辐射噪声机理的研究可集中于该机械内部叶片旋转过程中产生的气动噪声。气动噪声声源可以通过多极展开分解为单极子噪声源、偶极子噪声源和四极子声源，即旋转叶片表面上任一微元的厚度源、力源和黏滞应力源分别对应单极子源、偶极子源和四极子源。因此，在线性条件下，旋转过程中流激振动引起的外部辐射噪声，就是由叶片上所有微元处的单极源、偶极源在壳体外部辐射噪声场的叠加。

国内上海交通大学的钟芳源教授、清华大学的居鸿宾等对旋转运动点声源近场声学频域解进行了研究［13］。2000年，西安交通大学的吴九汇从理论上推导出了自由空间旋转点源的声场［14］，并进一步研究了旋转偶极声源的辐射声场。同年，吴九汇采用覆盖域的概念，给出了任意形状封闭薄壳的内部散射声场的统一表达式，并用互易原理求解封闭薄壳在外力作用下的内部声场［15］。2003年，吴九汇从球坐标中的声波波动方程出发，利用本征函数展开方法和界面边界条件，导出了双层弹性封闭球壳的内部散射声场表达式［16］。2006年，时胜国等以实际应用需求为背景，从理论上分析了平面声波在弹性球壳上的衍射声压场［17］。2010年，刘志红应用运动媒质声学理论和克希荷夫积分方法，从运动声源声辐射预估模型和声场特性两个方面对声辐射预估理论进行了深入研究［18］。2012年，夏琳琳利用解析法以及有限元法，以球壳、圆柱壳和两端带帽加肋圆柱壳为例，研究分析了点激励下辐射声场的标量及矢量特性［19］。

本文在此基础上，利用声学互易定理，对简单封闭薄壁球壳作旋转运动时的辐射声场进行了研究。

1 声学互易定理

声学互易定理［20］将两个声源的声场联系起来，它适用于线性系统，满足声场的叠加原理，即由声源和表面振动产生的空间任一点的声场进行叠加而互不影响。

如图1所示，当空间存在弹性物体或弹性壳体时，物体表面S与无限大半径的球面S′围成的声场体积为V，q1（r）和q2（r）为两个声源，f1（r）和f2（r）为两个分布力。

图1 弹性表面在声源和力作用下的互易原理示意图

弹性表面在一个简单声源q1（r）和一个外力f2（r）的作用下，空间任一点rt（rt，θt，φt）处的辐射声压P2（r，rt）和q1（r）声源作用下的散射声场P1（r，rt）之间的关系可表示为

2 封闭薄壁球壳散射声场计算

根据声学互易定理，为了求解封闭薄壁球壳在外力作用下的辐射声场，首先要求解散射声场。选取球坐标系（r，θ，φ），使薄壁球壳中心和坐标原点重合，球壳半径为R，如图2所示。假设在薄壁球壳内部任意一点r0（r0，θ0，φ0）处存在一单位强度的点声源q。由于声源q的作用，球壳内部的散射声场可以表示为［21］

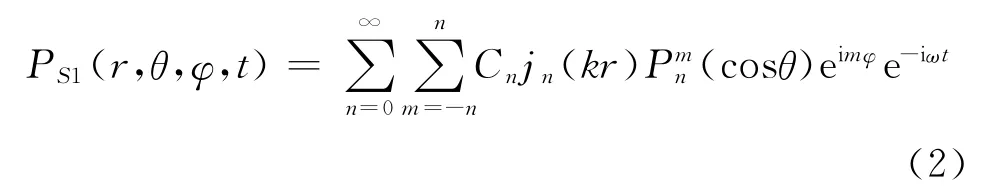
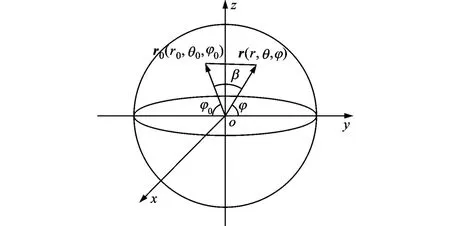
图2 封闭薄壁球壳内部声散射示意图

球壳外部辐射声场为

式（2）和（3）中：Bn、Cn为待定系数；波数k=ω／c，c为声速（kr）为第一类Hankel函数；（cosθ）为第一类Legendre函数。下面用薄壁球壳径向位移方程以及边界条件来确定Bn、Cn的值。根据文献［15］、［22］、［23］，由薄壁球壳径向位移满足的六阶方程，以及薄壁球壳与周围介质在交界面上满足的边界条件可确定Bn和Cn的值

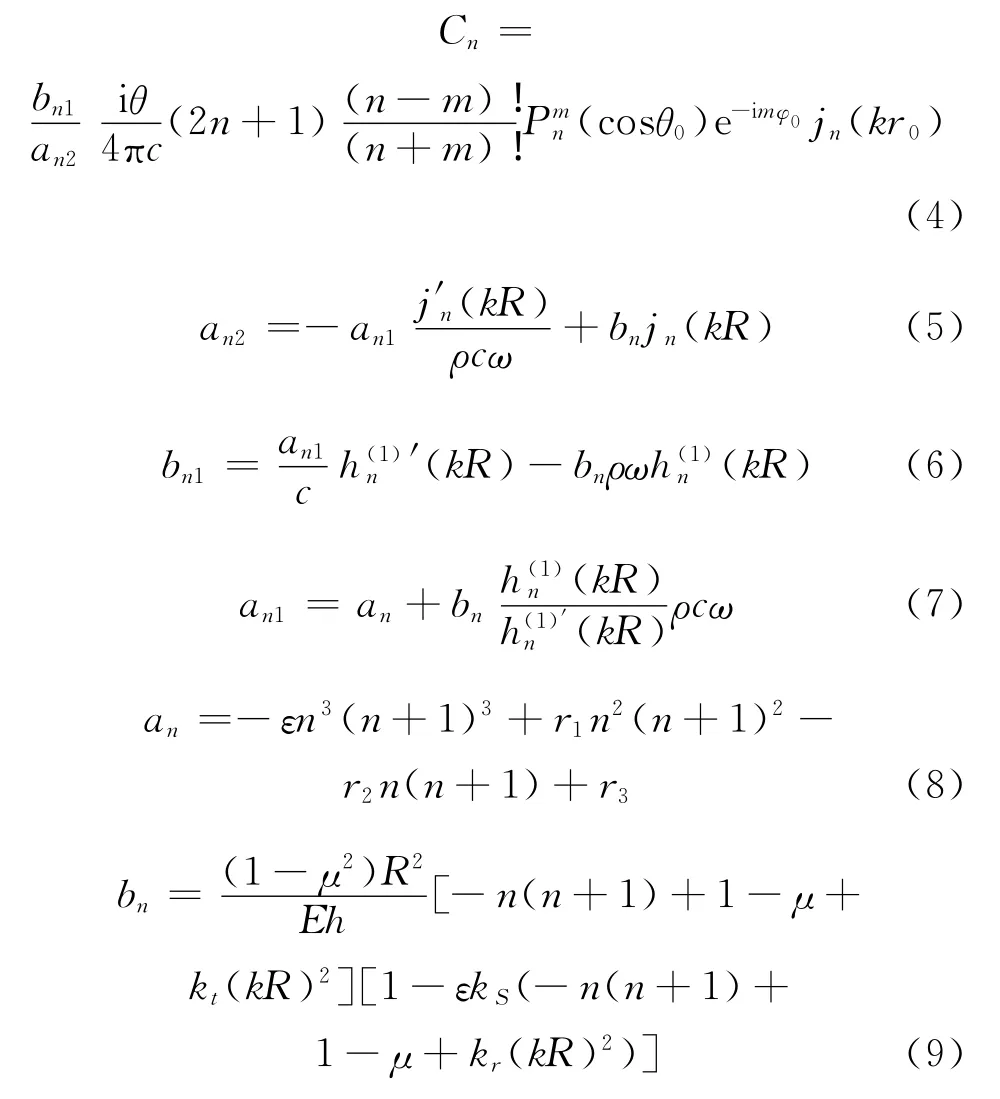
式中：jn（kR）为球Bessel函数；h为球壳厚度；R 为封闭球壳半径；μ为波松比；k=ω／c为波数；ω为声场角频率；c为声速；ε=h2／12R2；kt=1+ε；kr=1+3h2／20R2。

同理，可以得到在封闭薄壁球壳外部某一点r1（r1，θ1，φ1）处存在一单位强度点声源时，外部任一点r（r，θ，φ）处的散射声场的表达式，即

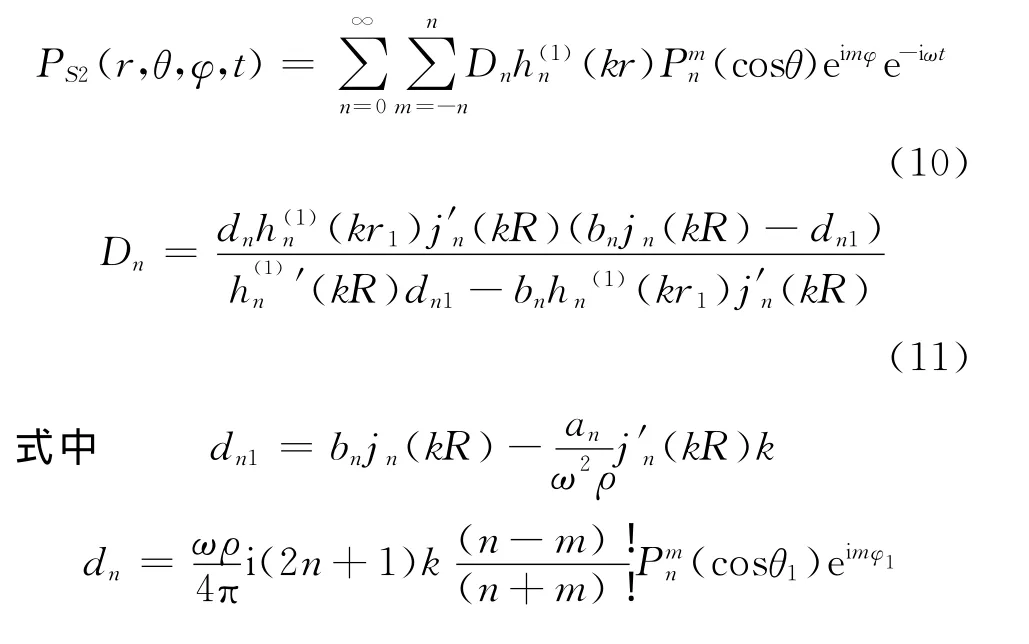
3 旋转薄壁球壳的空间辐射声场

前面的计算中，都是以薄壁球壳自身的球心为坐标原点而建立的空间球坐标系。要研究薄壁球壳围绕一个固定旋转轴作旋转运动，就要计算旋转辐射声场，而且要对坐标系进行转换。

3.1 空间坐标系的转换

如前所述，在应用式（10）求解声场中某一点A的散射声场时，得到的结果只是局部坐标下的散射声场。下面进行坐标系的转换，如图3所示。

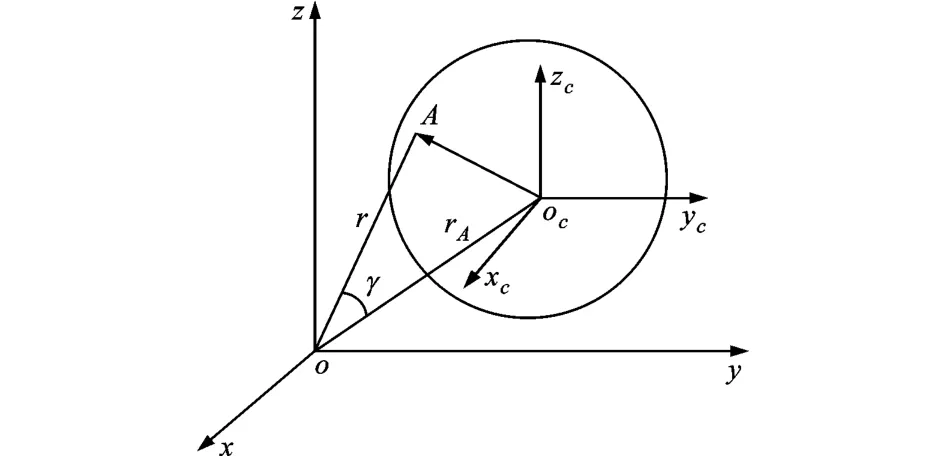
图3 空间坐标系转换示意图

图中oxyz为空间直角坐标系，ocxcyczc为空间局部直角坐标系。点oc为旋转薄壁球壳的球心坐标为（xc，yc，zc），相应的球坐标为（rc，θc，φc），则空间任一点A在oxyz坐标系中的坐标为（x，y，z），相应的球坐标形式为（r，θ，φ）。经过数学计算可求解出点A在ocxcyczc坐标系中的表达式。

因此，将局部坐标下的散射声场转换为全局坐标下的散射声场的表达式为

3.2 旋转薄壁球壳空间辐射声压计算

对于任意运动物体的声场结构，可由FW-H方程描述［5］。假设声源处于无限空间中，声学介质静止且场是准定常的。首先建立坐标系，设观察点位置和时间坐标分别为X，t；在此声学环境中有一运动声源分布V（τ），其强度为P（r，τ）；此运动声源的位置和时间坐标分别为ξ和τ，此声源产生的声压为

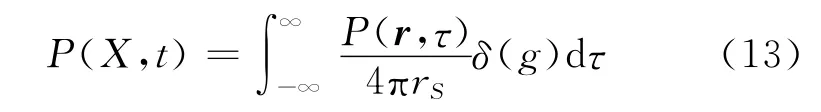
式中：rS=|X-ξ（τ）|表示源到观察点间的距离；g=t-τ-rS／c为延迟时间。对上式做傅里叶变换［24］，可得任意运动声源声场的频域解

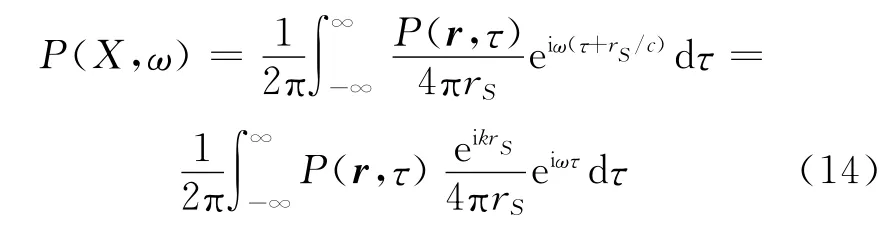
下面讨论封闭薄壁球壳作为声源在做旋转运动时的情形。采用如图4所示的球坐标系，假设薄壁球壳在xy平面内旋转，坐标原点取在旋转中心处，z为极轴，也是旋转轴，又设薄壁球壳初始位置在rb处，即球心在rb（r，π／2，φb）处，空间观察点 A 在r0（r0，θ0，φ0）处。任意时刻τ，薄壁球壳旋转运动到r处，即球心位置移到r（r，π／2，φ）处，若其旋转角频率为Ω，则φ=φb+Ωτ，rS=+r2-2r·r0cosβ）1／2为旋转薄壁球壳球心到观察点的距离，β为r0和r之间的夹角。

图4 薄壁球壳旋转运动示意图

经过数学计算，式（13）可以改写为

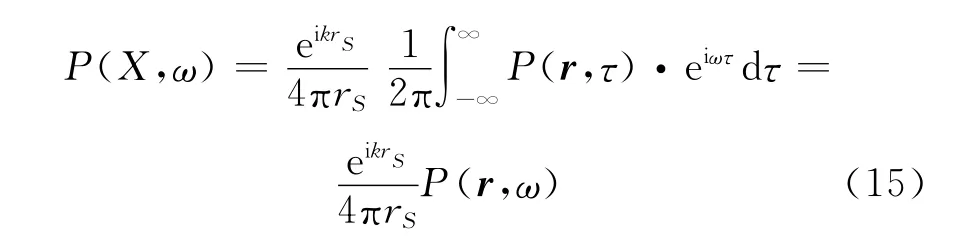
式中P（r，ω）是P（r，τ）的傅里叶变换。

根据文献［25］有如下公式

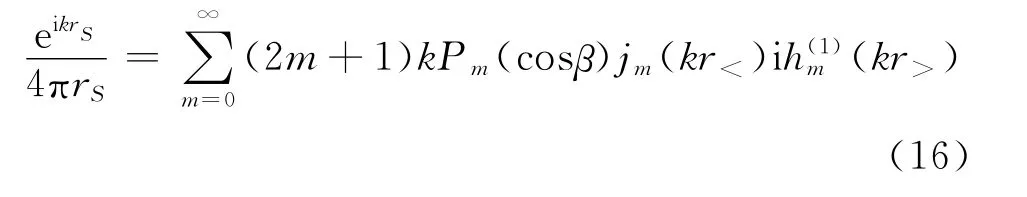
式中：r＜和r＞分别表示r和r0中的较小值和较大值。Pm（cosβ）可根据 Legendre函数的加法公式［25］展开如下

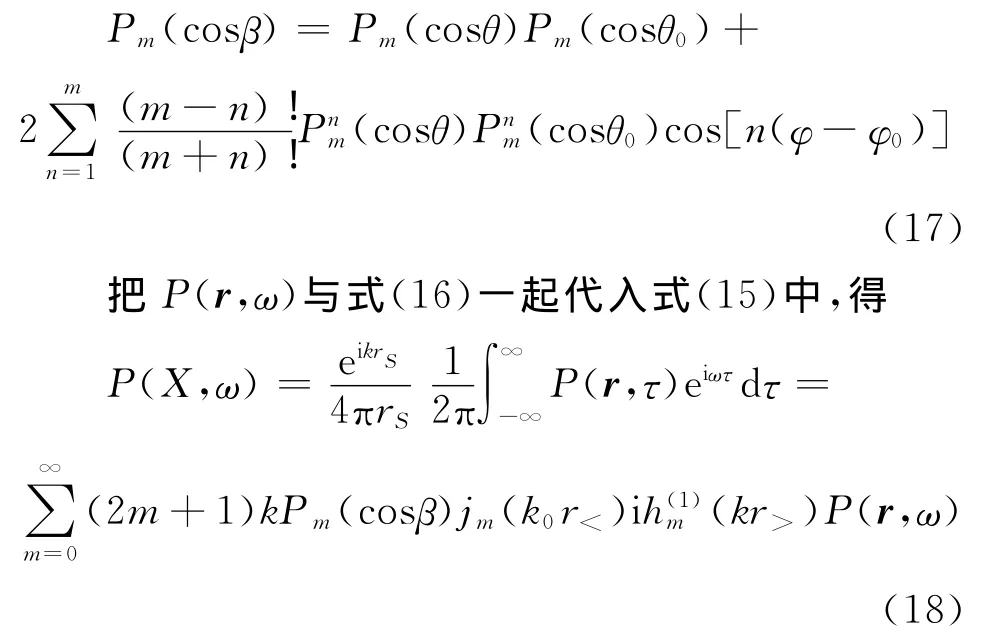
式（18）即为封闭薄壁球壳作旋转运动时空间任一点处辐射声压的计算公式。

3.3 旋转薄壁球壳空间辐射声压的实例计算

如图4所示，假设现有一封闭的薄壁球壳在自由空间做旋转运动，旋转平面在xy平面，旋转轴是空间坐标轴z轴。空间有一观察点A在ro（ro，θo，φo）处，球壳的初始位置在rb（r，θb，φb）处，在任意时刻τ球壳旋转运动到r（r，θ，φ）处，若旋转角频率为Ω，则有φ=φb+Ωτ。

计算实例中的各参数分别设定如下：球壳自身半径为R，球壳的壁厚为h=0.001m；球壳材质为钢球，已知钢材的密度为ρ=7 800kg／m3；弹性模量E=2.1×1011N／m2；泊松比μ=0.3；平均剪切系数ks=1.2；大气压强P0=1.013×105Pa；空气介质密度为ρ0=1.293kg／m3；声速c=340m／s；观察点位置坐标，r0=2.0m，φ0=-π／4；球壳的初始相位角为φb=0；球壳的旋转半径r=0.5m。针对不同的旋转频率ω0或不同的球壳半径，利用式（18）的公式进行以下3组计算：计算结果分别如图5、6、7所示，它们表示在不同观察角θ0处声压幅值的谐波分布。

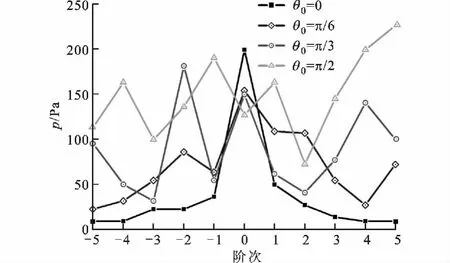
图5 旋转薄壁球壳辐射声压幅值的谐波分布（第1组计算）

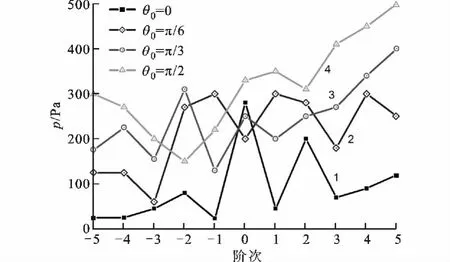
图6 旋转薄壁球壳辐射声压幅值的谐波分布（第2组计算）

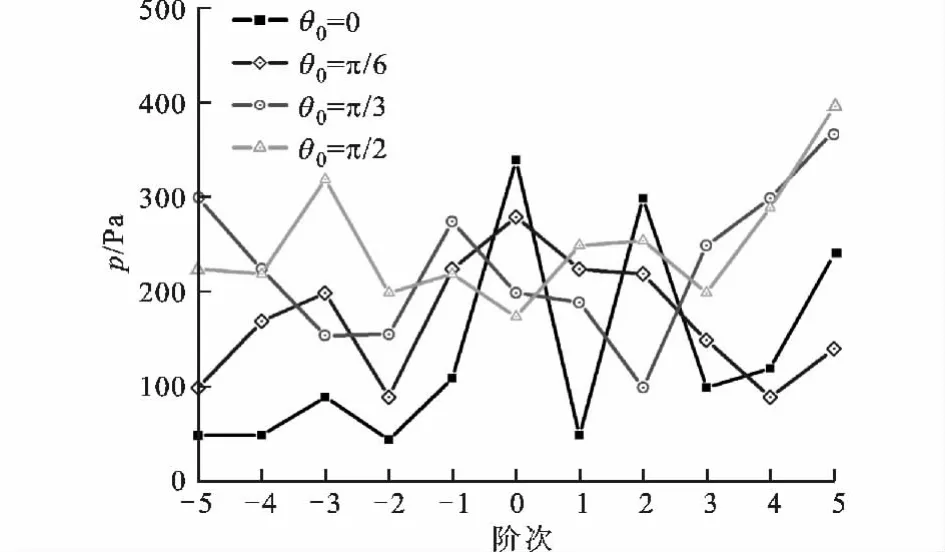
图7 旋转薄壁球壳辐射声压幅值的谐波分布（第3组计算）

由图可以看出，薄壁球壳旋转时产生的辐射声场受旋转频率和球壳半径影响比较大，可得如下的声场特性：

（1）随观察角θ0的增加，谐波分布越来越丰富，且对应的声压幅值在大部分区域都有所增强；

（2）旋转频率变化对谐波分布影响非常大，会出现明显的多普勒效应；

（3）θ0较小时，当旋转频率增大，谐波分布变化不大，θ0较大时，随着旋转频率增大，声压幅值谐波分布更加丰富，且声压幅值明显增大；

（4）当旋转频率保持不变时，随着薄壁球壳半径的增大，在所有θ0范围内，声压幅值都有所加强，谐波分布也愈丰富。

4 任意复杂形状旋转封闭薄壳空间辐射声场

前面主要针对封闭的薄壁球壳展开研究，但在一般情况下，面对的都是一些复杂形状的壳体结构，此时就不能直接、简单地应用前文的推导结果来计算、分析旋转辐射声场及声振耦合的问题。为此，引入覆盖域的方法［15，26］，结合上文中简单封闭球壳的散射声场来求解出任意复杂形状的封闭薄壳的散射声场［15］，并在此基础上，运用上文对旋转薄壁球壳辐射声场的分析方法进一步给出复杂形状封闭薄壳旋转时的辐射声场的计算方法。

根据覆盖域方法的基本原理，假设任意复杂形状封闭薄壳的边界是P，一般情况下，该边界P总是可以看作是由若干片球面P1，P2，…，Pk，…，Pn（k=1，2，3，…，n）拟合而成的。根据覆盖域的思想，现有n个组成复杂形状薄壳B的覆盖球壳Bk（k=1，2，3，…，n），其中每一个覆盖球壳Bk都完全覆盖了整个薄壳B，并且该覆盖球壳有且仅有一片边界MBk与球面发生重合。这样n个覆盖球壳的共同区域，即它们的交集，就组成了任意复杂形状的封闭薄壳。

利用覆盖域的思想，可将任意复杂形状封闭薄壳的散射问题转化为简单薄壁球壳散射声场的叠加问题。薄壁球壳的散射声场计算，在上节中已经得到，因此任意复杂形状封闭薄壳的散射声场可以表示为

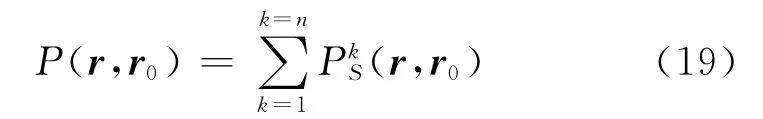
至此，就可以运用简单薄壁球壳旋转运动时辐射声压的求解方法与步骤，推导出复杂封闭薄壳旋转运动的辐射声场。

5 总 结

本文主要研究了封闭薄壁球壳旋转运动时的辐射声场问题。在封闭薄壁球壳的内、外部散射声场的基础上，利用声学互易定理和气体动力学的基本理论，推导出了封闭薄壁球壳做旋转运动时的辐射声场计算公式，并用该公式对一具体的旋转薄壁球壳进行了实例计算，得出了旋转薄壁球壳的一些声场特性。在此基础上，通过覆盖域方法，给出了一种可计算任意复杂形状旋转封闭薄壳辐射声场的思路和方法。这一研究为任意旋转声源辐射声场的定量分析提供理论基础，也为旋转机械气动噪声内在机理的研究提供了一种新的思路与方法。

［1］ LIGHTHILL M J.Sound generated aerodynamically［J］.Mathematical and Physical Sciences，1962，267：147-182.

［2］ LIGHTHILL M J.On sound generated aerodynamically ［J］.Proceedings of the Royal Society，1952，211：564-587.

［3］ LIGHTHILL M J，GUTIN L.On sound generated aerodynamically ［J］.Turbulence as a Source of Sound，1954，222（1148）：1-32.

［4］ CURLE N.The influence of solid boundaries on aerodynamic sound ［J］.Mathematics and Physical Sciences，1955，231（1187）：505-514.

［5］ WILLIAMS J E，HAWKINGS D L.Sound generation by turbulence and surface in arbitrary motion ［J］.Mathematics and Physical Sciences，1969，264：321-342.

［6］ POWELLl A.Theory of vortex sound［J］.Journal of Acoustic Society of America，1964，36（1）：177-179.

［7］ POWELL A.Aerodynamic noise and the plane boundary ［J］.Journal of Acoustic Society of America，1960，32（8）：982-990.

［8］ HOWE M S.Lectures on the theory of vortex-sound［C］∥ Sound-Flow Interactions.Berlin：Springer Press，2002：31-110.

［9］ HOWE M S.Theory of vortex sound ［M］.New York：Cambridge University Press，2003：1-216.

［10］LOWSON M V，The sound field for singularities in motion ［J］.Mathematical and Physical Sciences，1965，286（1407）：559-572.

［11］FRANCESCANTONIO P.A new boundary integral formulation for the prediction of sound radiation ［J］.Journal of Sound and Vibration，1997，202（4）：491-509.

［12］FARASSAT F，EMYERS M K.Extension of Kirchhoffs formulation to radiation from moving surface［J］.Journal of Sound and Vibration，1988，123（3）：451-460.

［13］居鸿宾，沈孟育，钟芳源.旋转运动点声源近场声学频域解 ［J］.声学学报，1996，21（3）：211-216.

JU Hongbin，SHEN Mengyu，ZHONG Fangyuan.Near field acoustic solution of a rotating point source in frequency domain［J］.Acta Acustica，1996，21（3）：211-216.

［14］吴九汇，陈花玲，黄协清.旋转点声源空间声场的频域精确解 ［J］.西安交通大学学报，2000，34（1）：71-75.

WU Jiuhui，CHEN Hualing， HUANG Xieqing.Acoustic solution of rotating point source in frequency domain［J］.Journal of Xi’an Jiongtong University，2000，34（1）：71-75.

［15］吴九汇，陈花玲，胡选利.任意形状封闭薄壳内部声场计算的一种新方法研究 ［J］.声学学报，2000，25（5）：468-471.

WU Jiuhui，CHEN Hualing，HU Xuanli.A new method to calculate interior sound field of arbitraryshaped closed thin shell［J］.Acta Acustica，2000，25（5）：468-471.

［16］吴九汇，王耀俊，陈花玲.双层弹性-非弹性封闭腔体的内部声场研究 ［J］.振动工程学报，2003，16（1）：29-35.

WU Jiuhui，WANG Yaojun，CHEN Hualing.Research on double layer elastic-inelastic closed cavity interior sound field ［J］.Journal of Vibration Engineering，2003，16（1）：29-35.

［17］时胜国，杨德森，王三德.弹性球壳声衍射对矢量传感器测量影响 ［J］.哈尔滨工程大学学报，2006，27（1）：84-89.

SHI Shengguo，YANG Desen，WANG Sande.Influence of sound diffraction by elastic spherical shell on acoustic vector sensor measurement ［J］.Journal of Harbin Engineering University，2006，27（1）：84-89.

［18］刘志红.声辐射预估理论及其应用研究 ［D］.青岛：青岛理工大学，2010.

［19］夏琳琳.水下壳体辐射声场特性研究 ［D］.哈尔滨：哈尔滨工程大学，2012.

［20］［苏］E JI沈杰罗夫.水声学波动问题 ［M］.何祚镛，赵晋英，译.北京：国防工业出版社，1983.

［21］吴九汇.噪声分析与控制 ［M］.西安：西安交通大学出版社，2011：48-50.

［22］PRASAD C.On vibration of spherical shells ［J］.Journal of Acoustic Society of America，1964，36（3）：489-494.

［23］吴九汇.车辆内腔声固耦合分析的覆盖域方法研究［D］.西安：西安交通大学，2000.

［24］汪德新.数学物理方法 ［M］.北京：科学出版社，2006.

［25］王竹溪，郭敦仁.特殊函数概论 ［M］.北京：科学出版社，1965.

［26］王良国，林晓.弹性力学中Fredholm积分方程组解法的表达通式及其讨论 ［J］.力学学报，1987，19（4）：323-331.

WANG Liangguo，LIN Xiao.General expression of Fredholm integral equations method on elastic mechanics and its discussion［J］.Chinese Journal of Theoretical and Applied Mechanics，1987，19（4）：323-331.

［本刊相关文献链接］

田福庆，罗荣，李万，等.改进的卷积型小波包分解及在故障诊断中的应用.2014，48（3）：89-95.［doi：10.7652／xjtuxb 2014 03017］

徐胜军，韩九强，何波，等.融合边缘特征的马尔可夫随机场模型及分割算法.2014，48（2）：14-19.［doi：10.7652／xjtuxb 201402003］

张西宁，郭金良，吴吉利.分数阶域滤波在启停车过程转频振

动分量提取中的应用.2013，47（11）：92-96.［doi：10.7652／xjtuxb201311017］

刘光辉，任庆昌，孟月波，等.自适应先验马尔可夫随机场模型的图像分割算法.2013，47（10）：62-67.［doi：10.7652／xjtuxb201310011］

董帆，陈启明，于跃平.旋转声源延迟时间方程求解的数值研究.2013，47（7）：120-123.［doi：10.7652／xjtuxb201307 022］

安跃军，张强，李文瑞，等.新型移相式屏蔽电动机屏蔽套涡流与温升分析.2014，48（6）：50.［doi：10.7652／xjtuxb201406 009］

赵曙，朱惠人，郭涛，等.出流比及旋转数对回转通道流动换热的影响.2014，48（6）：117-121.［doi：10.7652／xjtuxb2014 06020］

刘瑞玲，钟德星，韩九强.汽车伞齿轮多目视觉检测系统与算法.2014，48（4）：1-7.［doi：10.7652／xjtuxb201404001］

张超，陈天宁，王小鹏，等.颗粒阻尼线性离散元模型参数的选取方法.2014，48（3）：96-101.［doi：10.7652／xjtuxb2014 03018］