水平集与灵敏度分析相结合的流体形状识别与优化方法

刘小民，张彬，张卓飒

（西安交通大学能源与动力工程学院，710049，西安）

流体形状识别是反问题中的一个重要的研究方向，在生物医学领域的心脏结构反演、血管形状设计及病变检测等问题中广泛应用。带有拓扑变化的形状识别问题是一类具有特殊目标函数的拓扑优化问题。拓扑优化不依赖于给定结构形状或拓扑的优化设计方法，最早用于解决基于固体力学原理的结构优化设计问题，主要包括均匀化法、变密度法、变厚度法、独立连续映射法、渐进结构优化法和水平集方法等［1］。水平集方法于1988年提出，Osher等在提出水平集方法的同时给出了求解水平集方程高精度的稳定数值解法［2］。在基于固体力学的拓扑优化研究领域，最早把水平集方法引入其中的是Sethian和Wiegmann，他们根据计算获得的von Mises应力进行了水平集方程的求解［3］。将水平集方法与灵敏度分析相结合，可使水平集方法在处理优化问题时更加简便、准确［4－6］。

随着结构拓扑优化在固体力学领域的发展，流体拓扑优化由Borrvall等应用变密度方法得以实现［7］。但是，变密度方法会产生中间密度材料，这使得基于变密度方法的流体拓扑优化很难得到较为精确的结果。最近，Duan等运用一种无需重新初始化的变分水平集方法分别针对二维Stokes流动及Navier－Stokes流动进行了拓扑优化，实现了基于变分水平集方法的流体拓扑优化［8］。Zhou等应用传统水平集方法对稳态二维及三维Navier－Stokes流动实施了拓扑优化，并主张每一次优化都要重新进行网格划分和法向速度扩展［9］。Challis等针对二维和三维Stokes流动进行了拓扑优化，但由优化方法得到的边界并不光滑［10］。Duan等应用变分水平集方法对Stokes流动形状识别问题进行了研究［11］。Chantalat等在Cartesian网格上运用一种罚方法与水平集方法相结合的方法进行了流体形状识别和形状优化［12］，但该方法仍然存在优化所得边界不光滑以及不易解决复杂流动等缺点，对含有梯度项的法向速度的直接求解不够准确，也无法直接加入无滑移边界条件。

本文研究的目的是，通过提出一种新型的法向速度扩展方法和无需样条参数化的重新网格划分方法，来改进水平集优化方法，通过求解Navier－Stokes和Stokes流动形状识别问题，来验证改进水平集优化方法的有效性。

1 数学模型

1．1 问题描述

设Ω是一个具有Lipschitz连续边界Γ＝∂Ω的有界开区域，代表流体域，则二维不可压缩的Navier－Stokes方程如下

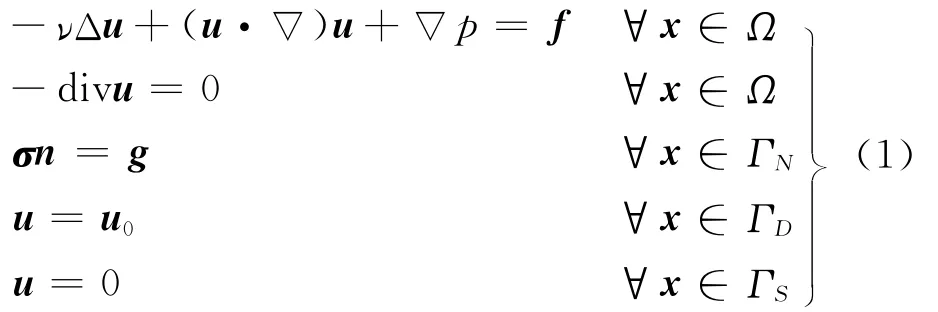
式中：Γ＝ΓN∪ΓD∪ΓS，并且ΓN、ΓD和ΓS两两之间无重合部分；ν是动力黏性系数；f是体积力；u0是边界ΓD上已知的速度分布；σ＝ν▽u－pI。如果式（1）中的对流项（u·▽）u被略去，则二维不可压缩Stokes方程如下

由此，形状识别问题可描述为

式中：u是满足状态约束式（1）或式（2）的速度分布；ud是已知的速度分布；D是优化问题的工作区域，对于所有可能的Ω均有Ω∈D。

1．2 灵敏度分析

定理1 设Ω是一个具有光滑边界Γ＝∂Ω的有界开区域，h∈W1，∞（R2，R2），其中R是实数集，Navier－Stokes流动形状识别问题的目标函数的Eulerian导数为［9］

式中：u是式（1）的解；w是如下共轭方程的解。该共轭方程如下

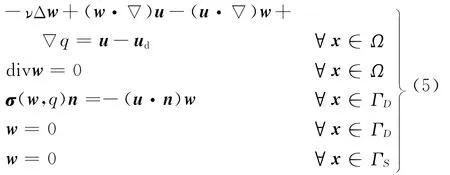
定理2 设Ω是一个具有光滑边界Γ＝∂Ω的有界开区域，h∈W1，∞（R2，R2），其中R是实数集，Stokes流动形状识别问题中目标函数的Eulerian导数为［13］

式中：u是式（2）的解；w是如下共轭方程的解。该共轭方程如下

综上，水平集演化方程为下面的Hamilton－Jacobi方程，即

式（8）中的水平集法向速度Vn应该由以上的灵敏度分析结果确定。由定理1可以提取Navier－Stokes流动形状识别问题的水平集法向速度，即

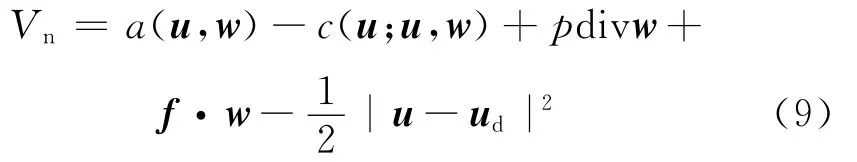
由定理2可以确定Stokes流动形状识别问题的水平集函数演化的法向速度，即

式中：“∶”表示双点乘运算。

2 改进的水平集方法

2．1 水平集函数的演化

水平集方法有许多优点［14］：容易描述边界法向及曲线等几何特征，可以很好地控制演化过程中的拓扑变化，能方便地应用偏微分方程描述，容易进行数值求解。

水平集函数φ（x，t）在演化过程中满足的方程如下

在流动形状识别问题中只有界面处的Vn有物理意义，为了在整个工作区域上求解式（11），应进行法向速度扩展。

2．2 法向速度扩展

文献［15］利用快速行进法进行了法向速度扩展，此方法在近界面处可以得到较准确的扩展结果，所求解的偏微分方程如下

虽然由文献［15］可以得到靠近界面处节点上的法向速度，但是实施起来比较困难，特别是当由本层节点寻找下一层节点位置时，实施过程很繁琐。本文将此方法用于流体第一层节点到固体第一层节点上的法向速度的扩展，对于整个水平集函数求解区域的扩展，可以通过以下方程来实现［16］

式（13）为全场扩展方法，基本思想是：将界面处的q值沿界面法向向两侧传播。由式（13）的特点可知，远离界面节点上的q都是以靠近界面处节点上的q为参考的，q＝Vn即可表示水平集法向速度的扩展。

将式（12）、式（13）结合起来，先在流体域直接求出边界上较准确的水平集法向速度，然后运用快速行进法将法向速度由流体域向未定义的固体域扩展，最后再运用求解偏微分方程的方法向整个水平集函数求解区域进行扩展。可见，本文方法在不做其他处理的情况下，直接、较准确地求出边界上的法向速度，且将界面附近的法向速度十分准确地沿界面的法线方向扩展到整个水平集函数求解区域。

3 数值方法

3．1 无需样条参数化的重新网格划分方法

本文采用的数值方法是无需样条参数化的重新网格划分方法，关键是在零水平集边界上直接进行三角网格划分。不失一般性且便于表述，以二维问题为例描述如下。

当已知网格节点rk－1的坐标（xrk－1，yrk－1），求下一个三角网格节点rk的坐标（xrk，yrk）时，先确定rk所在的四边形单元。如果rk－1与rk的距离为Δdk－1，则rk满足

式中：φrk为rk处的水平集函数值，rk所在单元的4个顶点a、d、f、e处的水平集函数值分别为φa、φd、φf、φe。设四边形单元内水平集函数值呈线性分布，则φrk值可由φa、φd、φf、φe进行双线性插值获得，即

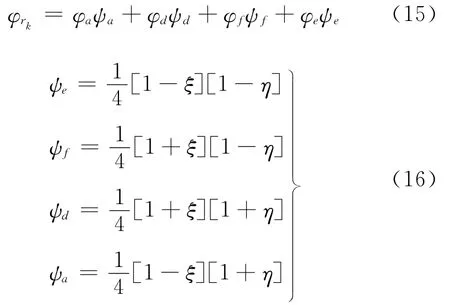
式中：ξ、η满足

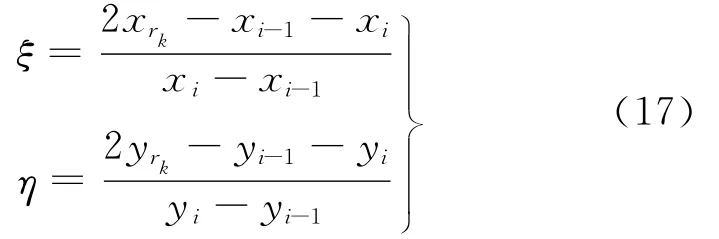
这样，式（14）变为

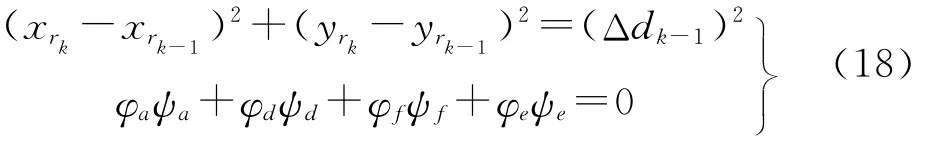
式（18）可以通过Newton迭代法等进行求解。在零水平集边界上划分出三角网格的边界节点后，就可以运用Delaunay等三角形化方法在流体域生成三角网格。

3．2 水平集方法的实施步骤

（1）给出初始的速度分布ud；

（2）给出初始区域Ω0，将Ω0初始化为符号距离函数；

（3）运用无样条参数化的重新网格划分方法在流体域划分出三角网格；

（4）利用非结构化网格上的有限体积方法求解状态方程（对于Navier－Stokes流动形状识别问题需要求解式（1），对于Stokes流动形状识别问题需要求解式（2））的速度u与压力p，进一步求解共轭方程（对于Navier－Stokes流动形状识别问题需要求解式（5），对于Stokes流动形状识别问题需要求解式（7））得到w和q；

（5）求取目标函数J（u，Ω），判断目标函数值是否收敛，如果收敛结束程序，否则运行步骤（6）；

（6）由式（9）（或式（10））求取水平集法向速度，并按照式（13）进行法向速度扩展；

（7）在结构化网格上运用差分方法求解水平集方程，并进行水平集函数的演化；

（8）3次优化迭代后进行1次水平集函数重新初始化，然后回到步骤（3）进一步循环，直到收敛为止。

3．3 有效性验证

在水平集拓扑优化中，物理场的求解主要有重新网格划分和浸没边界方法，本文采用重新网格划分方法。为了验证重新网格划分方法的有效性，分别采用重新网格划分和浸没边界这2种方法对Stokes方程进行求解。

根据雷诺准则，任意2个符合雷诺准则的流动，只要满足雷诺数相同条件，其流动情况一致。本文研究的流动问题均满足雷诺准则，所以算例中只给出了流动雷诺数。考虑到对称性，特征尺度L为1／2进口宽度，特征速度U 为进口处平均速度。将研究问题的工作区域D描述为四边形区域，流体域用Ω表示。在区域D的4条边界ΓD上均给定Dirichlet边界条件，速度为常量。如果以u＝（u1，u2）表示速度，那么u＊＝u／U＝（u＊1，u＊2）＝（u1／U，u2／U）在4条边界上均有u＊1＝1、u＊0＝0，Ω与固体域的交界面则看作具有无滑移边界条件的边界ΓS。优化问题的目标函数为式（3），状态约束为式（2），流场求解区域为串列双圆绕流区域，如图1所示，由定理2给出目标函数的灵敏度分析结果。

图1 Navier－Stokes流动形状识别问题的目标流场

运用重新网格划分和浸没边界方法求解串列双圆绕流问题时采用的网格分别如图2a和图3a所示。由图2a可以看出，采用重新网格划分方法时需先将双圆形状提取出来，然后在流体域进行适体网格划分。由图3a可以看出，浸没边界方法是在整个设计区域上进行网格划分且不需要提取边界。上述2种方法的网格划分都是采用Delaunay方法生成的，在区域外边界上的网格具有相同的边界节点数。重新网格划分和浸没边界方法求解双圆绕流问题时获得的速度矢量分布分别如图2b和图3b所示。由图3b可以看出，双圆附近出现了大范围的低速区，这与串列双圆实际流动状态不符。重新网格划分和浸没边界方法求解串列双圆绕流时获得的流线分布分别如图4和图5所示。由图4可以看出，重新网格划分方法求解双圆绕流时在界面附近获得了合理的流动分布，表明重新网格划分方法能有效提高物理场控制方程的求解精度。由图5可以看出，圆形界面处的流线没有沿圆的边界绕流，而是进入了固体域，这与Stokes流动的真实情况不符。

图2 重新网格划分方法的网格划分和速度矢量分布

图3 浸没边界方法的网格划分和速度矢量分布

图4 重新网格划分方法获得的串列圆形流线分布

图5 浸没边界方法获得的串列圆形流线分布

4 数值算例

4．1 Stokes流动形状识别问题

Stokes流动是一种典型流动，当Re较小时，Navier－Stokes方程中对流项（u·▽）u的作用很小，甚至可以忽略不计，此时Navier－Stokes流动可以当作Stokes流动进行处理。对于Stokes流动形状识别问题，目标形状仍然取图1所示的双圆形状，Re＝40。目标流场的速度矢量分布ud＝（ud1，ud2），如图6所示。

图6 Stokes流动形状识别问题的目标流场

一个四边形作为串列双圆形状识别问题的初始形状如图7a所示，迭代10、20和30步时获得的形状及速度分布如图7b～图7d所示，Stokes流动形状识别过程得到的最终形状如图7e所示。由图7可以看出：当迭代20步时，初始形状发生了拓扑变化，表明本文方法可以有效处理带有拓扑变化的优化问题，Stokes流动形状识别过程中得到的最终形状与目标形状很接近（见图6）。目标函数在形状识别过程中的变化如图8所示。由图8可以看出，初始迭代时目标函数变化较大，之后变化减缓，直至保持不变为止，由此获得最优结果。

4．2 Navier－Stokes流动形状识别问题

对于一个目标为双圆Navier－Stokes流动形状识别问题，其工作域、流体域、边界条件等与Stokes流动形状识别问题相同，优化问题的目标函数为式（3），状态约束为式（1），Re＝40。定理1给出了Navier－Stokes流动形状识别问题的灵敏度分析结果。一般情况下，目标流场的速度ud＝（ud1，ud2）是通过实验测得的，本文主要是验证方法的有效性，所以目标流场并未采用实验测量结果，而是通过数值计算结果获得的目标流场的速度分布。

串列双圆Navier－Stokes流动形状识别问题的初始形状如图9a所示，迭代10、20、30和40步时获得的形状及速度分布如图9b～图9e所示，最终获得的目标形状如图9f示。由图9可以看出：迭代40步时，初始形状发生了拓扑变化，表明本文方法可以处理带有拓扑变化的Navier－Stokes流动形状识别问题；随着迭代的继续进行，最终获得的形状与目标形状比较接近。目标函数在形状识别过程中的变化如图10所示。由图10可以看出：目标函数的变化一直呈下降趋势，最终达到最小值且保持不变。

图7 Stokes流动形状识别过程

图8 Stokes流动形状识别问题的目标函数变化过程

图9 Navier－Stokes流动形状识别过程

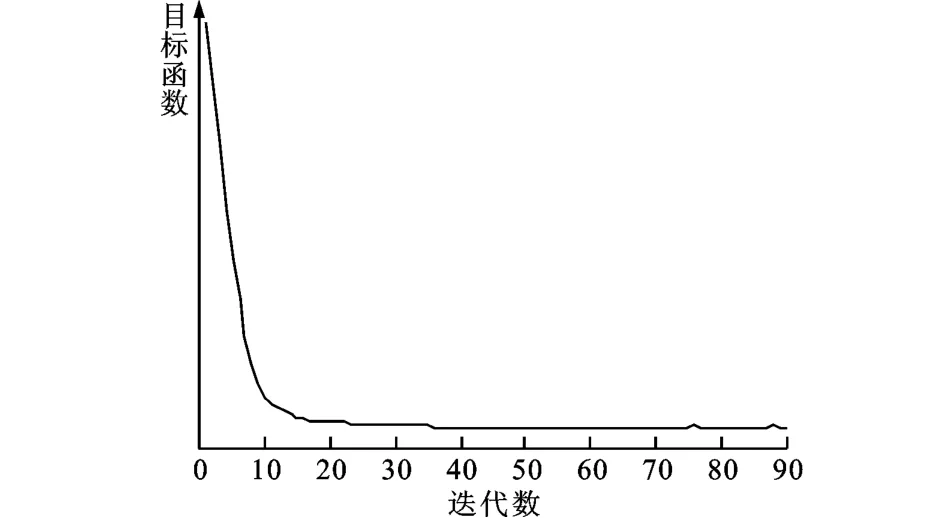
图10 目标函数在形状识别过程中的变化

比较图6和图9可以看出，当Re＝40时，Stokes和Navier－Stokes流动形状识别过程存在一定的差异。对于Navier－Stokes流动形状识别问题，迭代20步时尚未出现拓扑变化（见图6c）；对于Stokes流动形状识别问题，迭代20步时初始形状出现拓扑变化，由区域中间一个孔洞变成了两个孔洞（见图9c）。由图6e和图9f可以看出，相比Navier－Stokes流动形状识别，Stokes识别的最终结果更加接近目标形状，即使在相同Re下，Stokes识别与Navier－Stokes仍有区别，这是Navier－Stokes方程中存在对流项（u·▽）u引起的。相对于Stokes流动，Navier－Stokes流动中对流项对流动状态的影响较大，Navier－Stokes流动形状识别问题中对应的水平集法向速度的变化相对较大。当时间步长一定时，为了满足CFL条件，水平集方程求解需要对最大法向速度加以限制。最大法向速度相同时，Navier－Stokes流动形状识别问题的整体收敛速度较慢，因此在Navier－Stokes问题中，迭代40步后初始形状才会发生拓扑变化，而在Stokes问题中，迭代20步后初始形状即可达到拓扑变化。

从算例中还可以看出，本文Stokes和Navier－Stokes流动形状识别问题最后所获得的最优形状与实际形状存在一些差异。这种差异可能由以下原因引起的：①对于复杂的流动，梯度类优化方法的局部收敛性使得优化问题容易陷入局部极值，从以上算例的分析中可以看出，Stokes优化问题相比Navier－Stokes优化问题的收敛性更差；②本文目标流场的形状识别难度较高，在靠近流固界面处流动速度接近0，而在圆柱内部设定为0，这种速度分布无疑会给形状的准确识别带来一定的难度。针对Navier－Stokes和Stokes流动形状识别，尽管在收敛速度及与目标形状的吻合程度方面本文还存在一定的偏差，但最终都能获得与目标流场和目标形状吻合较好的结果，这也表明本文发展的方法能够有效处理流体形状识别问题。

5 结 论

（1）本文提出了水平集法向速度扩展方法，并将其与无需样条参数化的重新网格划分相结合，从而得到了一种较为精确的流体拓扑优化方法。运用此方法处理流体拓扑优化问题时，既可直接施加于流体边界，又可降低样条参数化等繁琐过程。

（2）对于 Navier－Stokes和Stokes流动形状识别问题，本文采用改进的水平集方法可以有效处理优化过程中的拓扑变化，可以直接优化得到光滑的边界，无需进行边界光滑化处理。

（3）对于 Navier－Stokes和Stokes流动形状识别问题，最终收敛的形状与目标形状有一定的偏差，造成这种偏差的主要原因是梯度类优化方法的全局性较差，但可以通过选择全局性较好的方法来解决。在梯度类优化领域，拓扑导数方法的全局性较好，用其进行形状识别可有效减小识别偏差，或者在本文优化结果的基础上，运用非梯度类的全局优化算法进一步进行优化，可以减小最优形状与目标形状的偏离。

［1］ 夏天翔，姚卫星．连续体结构拓扑优化方法评述 ［J］．航空工程进展，2011，2（1）：1－11．XIA Tianxiang，YAO Weixing．A survey of topology optimization of continuum structure［J］．Advances in Aeronautical Science and Engineering，2011，2（1）：1－11．

［2］ OSHER S，FEDKIW R．Level set methods and dynamic implicit surfaces［M］．Berlin，Germany：Springer，2003：1－258．

［3］ SETHIAN J，WIEGMANN A．Structural boundary design via level set and immersed interface methods［J］．Journal of Computational Physics，2000，163（2）：489－528．

［4］ WANG M Y，WANG X，GUO D．A level set method for structural topology optimization ［J］．Computer Methods in Applied Mechanics Engineering，2003，192（1／2）：227－246．

［5］ ALLAIRE G，JOUVE J，TOADER A M．A level set method for shape optimization ［J］．Comptes Rendus de l’Académie des Sciences：Series I，2002，334（12）：1125－1130．

［6］ ALLAIRE G，JOUVE J，TOADER A M．Structural optimization using sensitivity analysis and a level set method［J］．Journal of Computational Physics，2004，194（1）：363－393．

［7］ BORRVALL T，PETERSSON J．Topology optimization of fluids in Stokes flow ［J］．International Journal for Numerical Methods in Fluids，2003，41（1）：77－107．

［8］ DUAN X，MA Y，ZHANG R．Optimal shape control of fluid flow using variational level set method ［J］．Physics Letters：A，2008，372（9）：1374－379．

［9］ ZHOU S，LI Q．A variational level set method for the topology optimization of steady－state Navier－Stokes flow ［J］．Journal of Computational Physics，2008，227（24）：10178－10195．

［10］CHALLIS V J，GUEST J K．Level set topology optimization of fluids in Stokes flow ［J］．International Journal for Numerical Methods in Engineering，2009，79（10）：1284－1308．

［11］DUAN X B，MA Y C，ZHANG R．Shape－topology optimization of Stokes flow via variational level set method［J］．Applied Mathematics and Computation，2008，202（1）：200－209．

［12］CHANTALAT F，BRUNEAU C H，GALUSINSKI C，et al．Level－set，penalization and Cartesian meshes：aparadigm for inverse problems and optimal design［J］．Journal of Computational Physics，2009，228（17）：6291－6315．

［13］张彬．水平集方法的改进及其在流体形状最优控制中的应用 ［D］．西安：西安交通大学，2011．

［14］ADALSTEINSSON D，SETHIAN J A．The fast construction of extension velocities in level set methods

［J］．Journal of Computational Physics，1999，148（1）：2－22．

［15］PENG D，MERRIMAN B，OSHER S，et al．A PDE－based fast local level set method［J］．Journal of Computational Physics，1999，155（2）：410－438．

［16］陶文铨．计算传热学的近代进展 ［M］．北京：科学出版社，2000：1－427．

［本刊相关文献链接］

王芳梅，范虹．利用改进CV模型连续水平集算法的核磁共振乳腺图像分割．2014，48（2）：38－43．［doi：10．7652／xjtuxb 201402007］

高燕华，刘玉欢，喻罡．多尺度非参数化水平集的超声心动图分割．2013，47（2）：53－57．［doi：10．7652／xjtuxb201302009］

田辉，王琳琳，叶阳辉，等．应用改进粒子水平集法对液滴碰撞的数值研究．2012，46（1）：125－130．［doi：10．7652／xjtuxb 201201023］

田辉，王琳琳，叶阳辉，等．一种改进的高效粒子水平集法及其应 用．2011，45（11）：34－38．［doi：10．7652／xjtuxb201111 007］

李彦鹏，王焕然．低冲击能量液滴与球面碰撞沉积特性的数值研究．2009，43（7）：21－24．［doi：10．7652／xjtuxb200907005］

段现报，马逸尘，韩西安．变分水平集方法在Stokes问题形状识 别 中 的 应 用．2008，42（10）：1313－13．［doi：10．7652／xjtuxb200810025］