螺栓连接结构接触面刚度识别方法①

姜 东，史勤丰，费庆国，吴邵庆

(1．江苏省工程力学分析重点实验室，南京 210096;2．东南大学土木工程学院工程力学系，南京 210096)

0 引言

螺栓连接在机械结构中应用广泛，连接结构在预紧力和荷载作用下会产生多种力学效应，如粘合、微观滑移(局部滑移)和宏观滑移(整体滑移)等，在极端工况下，甚至会发生分离和拍击现象。但在预紧力足够大或者激振力幅值较小情况下，所发生的微观滑移能够线性化处理［1］。螺栓连接的有限元模拟方法主要分为2类:非线性接触算法和界面单元法［1－2］。前者需要不断通过接触算法判别接触状态，迭代计算结构响应，计算量较大。薄层单元属于界面接触单元的一种，最早来自于模拟岩石接触的力学分析［3－5］。近年来，国外已将薄层单元应用于焊接、螺栓连接等形式的机械连接建模中［6－8］。研究表明，薄层单元可准确模拟连接结构的力学特性，相对于接触算法计算效率较高，但需要通过试验得到接触面薄层单元的刚度参数，对不同方向的接触刚度需要分别进行试验，工作量较大;对试验装置、试验方法要求较高。国内方面，薄层单元的应用主要集中于岩土结构的分析，如金峰等［9］用薄层单元分析了重力坝体的抗震稳定性分析;黄耀英等［10］分析了基于横观各向同性体本构方程简化得到的薄层单元的本构方程;螺栓连接模拟方法方面，采用虚拟各向同性材料模拟固定连接界面的方法［11］，计算频率与试验值误差小于9%。黄开放等基于虚拟材料的方法［12］能够应用于预紧力变化的连接结构动力学仿真，其结果与试验值误差在±6%以内。接触面刚度对螺栓连接结构动态特性具有重要影响。

针对固定结合面的螺栓连接结构，本文提出了一种能够准确识别螺栓搭接结构接触面刚度性能的方法。在薄层单元基本理论基础上，对单个螺栓搭接和多个螺栓搭接2种结构进行有限元建模，接触界面采用基于正交各向异性本构关系的薄层单元模拟，根据试验模态参数，识别其材料参数。

1 基本理论

1．1 接触面力学性能

对于固定接触界面螺栓连接，外力作用下接触状态为粘合，或者仅发生微小的局部相对位移(微观滑移)，不会发生宏观滑移及分离等非线性效应，此时各接触面之间仅存在法向接触力和切向摩擦力，图1为螺栓连接接触面力学性能示意图。在此前提下，可近似地将接触刚度线性等效，建立具有线性本构关系的固定结合面单元，无需定义接触以及采用接触搜索算法来判断连接部位接触状态;进而在很大程度上简化接触面模拟和计算。采用薄层单元针对实际的接触状态建立结合面参数化模型，便于进行连接结构的参数识别。

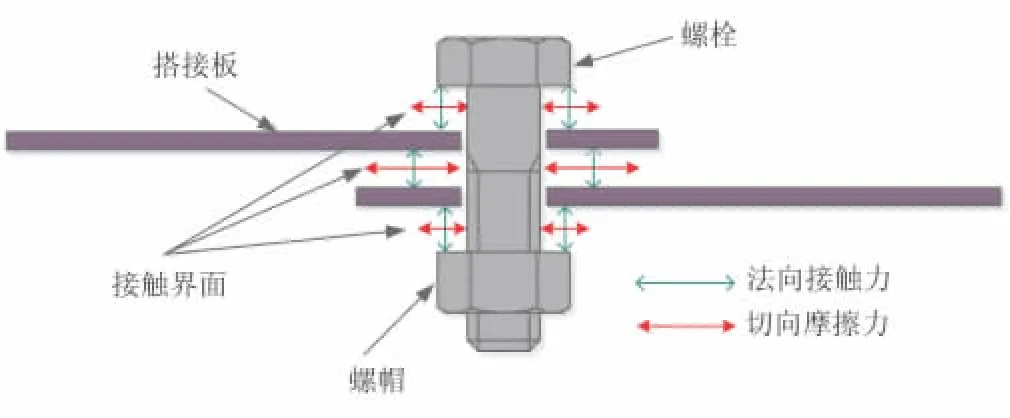
图1 螺栓连接接触面力学性能Fig．1 Mechanical properties of contact surface in bolted-joint

1．2 薄层单元理论

薄层单元最早由Desai等［3］提出，在相邻接触体之间，定义一层特殊单元来等效连接界面接触力学特征。

考虑尺寸为l1×l2×d的薄层单元，根据虚位移原理，得到如下的虚功方程:

其中，l1和l2是薄层单元在单元局部坐标系下x和y方向上的长度;d为z方向尺寸。通过等参变换计算薄层单元刚度矩阵K:

图2为薄层单元等参变换，其中ξ、η、ζ是自然坐标符号;J为雅克比矩阵。当自然坐标与局部坐标的坐标轴方向一致，J可表示为

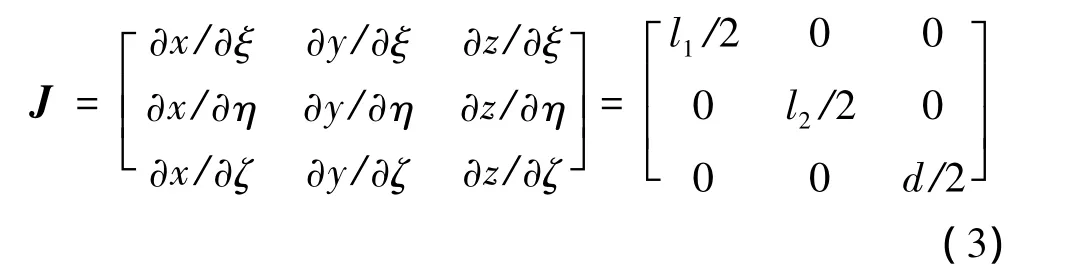
图2 薄层单元等参变换Fig．2 Iso-parametric transformation of thin-layer element

对于薄层单元，厚度d远小于另2个方向的特征尺寸 l1和 l2，单元的面内应变分量(εx，εy，γxy)和应力分量(σx，σy，τxy)将被忽略［3］。采用单元形函数进行分析［10］，∂Ni/∂z远大于 ∂Ni/∂x 和 ∂Ni/∂y(其中 Ni为单元形函数)，可认为 ∂Ni/∂x= ∂Ni/∂y≈0，从而得出应变分量εx=εy=γxy≈0。因此，薄层单元在高斯点上的应变分量只有3个不为零，应变分量简化为ε=［εzγyzγzx］T。将接触面的法向{e}n和2 个切向{e}t分别定义为薄层单元局部坐标系的z、x、y方向，假设连接界面法向和切向接触性能相互独立，2个切向的接触性能具有一致性，表征界面接触性能的薄层单元本构方程可表示为

总之，基于碳氟键断裂或活化的硼化反应作为新的氟化学和硼化学的交叉研究领域正日益引起人们的关注，新反应、新方法也层出不穷。我们相信将碳氟键的惰性与硼酯基团强大的反应能力相结合，一定会为药物的后阶段修饰策略 (the late-stage drug modification) 提供强有力工具。钯或铁催化的芳基氟的硼化反应[12]发表在Organic Letters, 2018, 20, 5564上，铜催化的偕二氟烯烃的硼化反应[14]发表在Organic Letters, 2017, 19, 3283上。该两项工作得到了国家自然科学基金和中国科学院有机氟化学重点实验室开放课题的支持。

其中，En、Gt分别是薄层单元的法向弹性常数和切向剪切模量，由连接结构接触面性能决定。若接触面的法向与切向接触性能相互耦合，可在本构关系式(4)中加入耦合项来实现［13］。

在有限元计算中，可采用正交各向异性材料本构关系模拟薄层单元，其本构方程为

正交各向异性材料共有9个独立的材料参数，3个方向的杨氏模量 E11、E22、E33，3 个泊松比 ν12、ν23、ν31，3 个剪切模量 G12、G23、G31。根据薄层单元的基本理论，εx=εy=εxy≈0，材料本构方程将退化为

此时，薄层单元仅采用3个独立的弹性参数E33、G23、G31来模拟接触性能。

2 薄层单元参数

2．1 单元厚度

薄层单元厚度对接触性能的描述有较大影响。若厚度过大，难以准确体现接触界面的力学特征;厚度过小，则会导致雅可比矩阵行列式的值趋向于零，矩阵病态，求逆困难，有限元求解时，无法计算位移-应变关系。对于厚度的选择，定义一个比例系数［3－4，13］:

2．2 接触刚度

薄层单元材料参数是螺栓连接结构有限元分析关键问题之一。对于接触面保持线性粘合状态的情况，弹性矩阵中的G和E都是常数［8］，一般通过试验得出，将其集成到薄层单元中，就能对连接结构进行准确的有限元动力分析。但对不同方向的接触刚度需分别进行测试，工作量较大;对试验装置、试验方法要求也较高。本文采用动态试验数据来识别连接结合面薄层单元的参数。

3 算例研究

采用单个螺栓和多个螺栓的搭接结构开展研究。基于螺栓搭接结构模态试验结果，将系统参数识别转化为优化问题，采用灵敏度分析方法，识别接触面薄层单元的正交各向异性本构关系材料参数。

螺栓搭接结构Ⅰ为1个螺栓的2块铝板搭接情况，螺栓搭接结构Ⅱ是2块铝板通过4个螺栓搭接而成。结构几何尺寸和搭接情况如图3所示，搭接板材料为铝合金，材料弹性模量E=6 800 MPa，密度ρ=2 800 kg/m3，泊松比 ν=0．33。

图3 螺栓搭接结构Ⅰ和ⅡFig．3 Bolted-joint structuresⅠ and Ⅱ

3．1 模态试验

对自由-自由状态下2种螺栓搭接结构的线性连接状态分别进行模态试验，得到前4阶横向振动模态参数。图4为螺栓搭接结构I、II前4阶振型和频率。

3．2 参数识别

建立了模型Ⅰ和模型Ⅱ的初始有限元模型，侧重整体连接结构的动态特征分析，忽略螺栓质量和螺孔的影响，主要考虑等效接触刚度模型。搭接板用实体单元，接触界面用正交各向异性本构关系的薄层单元模拟。

将薄层单元材料参数识别转化为优化问题［14］。建立的目标函数是前四阶弯曲振型的计算和试验结果残差加权平方和最小

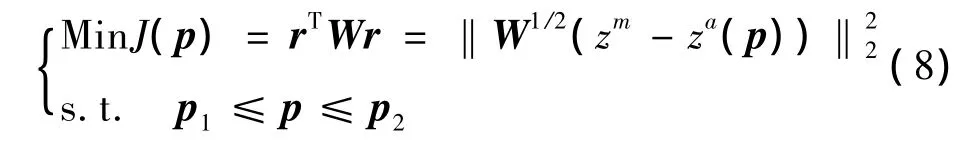
目标函数J(p)定义为在结构待识别参数合理取值范围p1≤p≤p2内，试验与计算模态参数的残差加权平方和取极小值。r为模态参数的残差，zm、za(p)分别为试验与计算的模态参数，加权矩阵W为反映各模态参数残差相对权重的对角阵。设定待修正参数的初值，采用灵敏度分析的方法，迭代求解优化问题(8)，第j个迭代步的问题描述为

式中 Sj=W1/2∂zj/∂pj为模态参数对待修正参数的加权灵敏度矩阵。

采用数值方法求解式(9)，可得pj+1，迭代直到待识别参数p收敛，且计算模态参数精度满足要求，则得到准确的接触面材料参数。

3．2．1 算例1——螺栓搭接结构Ⅰ

图5为螺栓搭接结构I有限元网格与结合面薄层单元示意图。图6为螺栓搭接结构I结合面薄层单元材料参数迭代收敛曲线。表1为薄层单元材料参数初始值和识别值。表2为参数识别前后计算与试验模态参数误差比较。

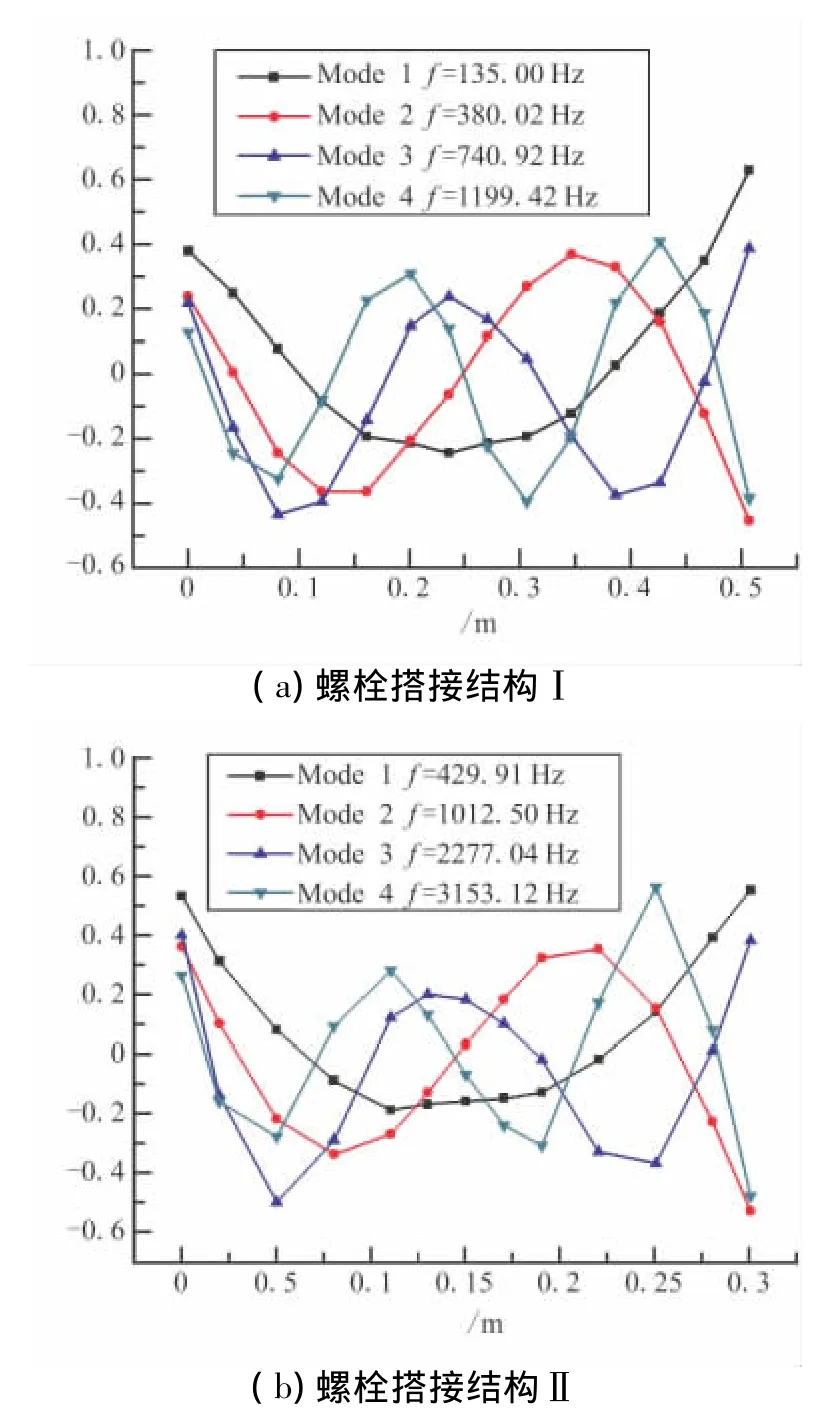
图4 螺栓搭接结构Ⅰ、Ⅱ前四阶试验振型和频率Fig．4 The first four mode shapes and modal frequencies of bolted-joint structureⅠandⅡ

根据接触面与螺栓的距离不同，将其等分为3部分，采用2种不同正交各向异性本构关系，模拟薄层单元，并进行参数识别。靠近螺栓的区域待识别参数为弹性模量 E33－1和剪切模量 G23－1，G31－1;远离螺栓的区域待识别参数为弹性模量 E33－2和剪切模量 G23－2，G31－2。薄层单元的厚度根据R=10来选取，密度取为0。

图5 螺栓搭接结构Ⅰ有限元网格与结合面薄层单元Fig．5 Finite element model of structure Ⅰ and thin-layer element of the contact surface

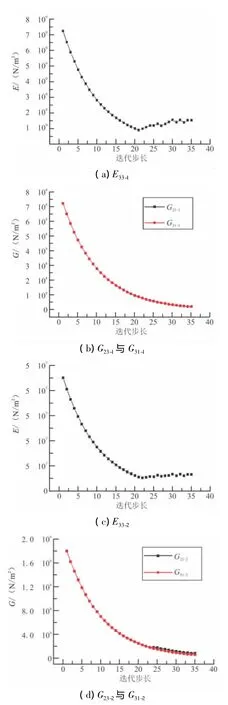
图6 螺栓搭接结构Ⅰ结合面薄层单元材料参数迭代收敛曲线Fig．6 Convergence of the material properties of thin-layer element in structureⅠ

表1 结构Ⅰ结合面薄层单元材料参数初始值和识别值Table 1 Initial and identified values of thin-layer element in contact surface of the structureⅠ

表2 结构Ⅰ参数识别前后计算与试验模态参数误差比较Table 2 Comparison of errors in modal data between before and after identification of the structureⅠ

识别后，固有频率的最大误差不超过3．5%，识别精度较高。从表1可见，两方向的剪切模量G23和G31基本一致，杨氏模量E33显著大于剪切模量G23和G31，能反映接触界面法向刚度大于切向接触刚度的特征;靠近螺栓区域的结合面材料参数识别结果大于远离螺栓区域，符合实际情况。因此，基于各向异性的薄层单元能反映出描述切向和法向接触性能之间的关系，并保证一定的计算精度。

3．2．2 算例2——螺栓搭接结构Ⅱ

螺栓搭接结构Ⅱ是2块铝板通过4个螺栓搭接而成。相对于结构Ⅰ，螺栓分布更为密集，接触情况更加复杂。采用2种薄层单元模拟接触界面。图7为螺栓搭接结构Ⅱ有限元网格与结合面薄层单元示意图。图8为螺栓搭接结构Ⅱ结合面等效虚拟材料参数迭代收敛曲线。表3为结合面薄层单元材料参数初始值和识别值。表4为参数识别前后计算与试验模态参数误差比较。

在约2倍螺杆直径的矩形区域内，定义虚拟正交各向异性材料1，待识别参数为弹性模量E33－1，剪切模量 G23－1、G32－1;在其他区域，定义虚拟正交各向异性材料2，识别参数为弹性模量 E33－2，剪切模量 G23－2、G31－2。薄层单元厚度同样根据R=10选取，材料密度取0。

识别后，计算模态频率最大误差不超过2．5%，识别精度较高。由表3可见，薄层单元材料的弹性参数在螺栓附近明显高于其他区域，且法向弹性模量大于剪切模量，与搭接结构接触面力学性能一致;由于螺栓较为密集，接触刚度分布容易受邻近螺栓的影响，识别的剪切模量 G23－1、G32－1有一定的差别，但依然能保证结构整体动态性的准确性。因此，基于虚拟各向异性材料的薄层单元，能较好地模拟多个螺栓搭接结构的连接性能。

表3 结构Ⅱ结合面薄层单元材料参数初始值和识别值Table 3 Initial and identified values of thin-layer element in contact surface of the structureⅡ

表4 结构Ⅱ参数识别前后计算与试验模态参数误差比较Table 4 Comparison of errors in modal data between before and after identification of the structureⅡ

图7 螺栓搭接结构Ⅱ有限元网格与结合面薄层单元Fig．7 Finite element model of structure Ⅱ and thin-layer element of the contact surface

4 结论

(1)对于2种螺栓连接结构，识别后计算模态频率最大误差均不超过3．5%，薄层单元参数能准确描述螺栓搭接结构的接触刚度。

图8 螺栓搭接结构Ⅱ结合面薄层单元参数迭代收敛曲线Fig．8 Convergence of the material properties of thin-layer element in structureⅡ

(2)采用2种不同性能的薄层单元模拟接触界面，参数识别结果符合接触面之间的力学关系，能较好地反映接触界面刚度分布不均匀性。

(3)本文方法适用于单个螺栓搭接和多个螺栓搭接等多种工况的有限元精确模拟及接触面刚度识别。

［1］ Bograd S，Reuss P，Schmidt A，et al．Modeling the dynamics of mechanical joints［J］．Mechanical Systems and Signal Processing，2011，25(8):2801-2826．

［2］ Yu H，Burgess I W，Davison J B，et al．Numerical simulation of bolted steel connections in fire using explicit dynamic analysis［J］．Journal of Constructional Steel Research，2008，64(5):515-525．

［3］ Desai C S，Zaman M M，Lightner J G，et al．Thin-layer element for interfaces and joints［J］．International Journal for Numerical and Analytical Methods in Geomechanics，1984，8(1):19-43．

［4］ Sharma K，Desai C．Analysis and implementation of thin-layer element for interfaces and joints［J］．Journal of Engineering Mechanics，1992，118(12):2442-2462．

［5］ Pande G N，Sharma K G．On joint/interface elements and associated problems of numerical ill-conditioning［J］．International Journal for Numerical and Analytical Methods in Geomechanics，1979，3(3):293-300．

［6］ Ahmadian H，Ebrahimi M，Mottershead J E，et al．Identification of bolted-joint interface models［C］//Proceeding of ISMA:Noise and Vibration Engineering Conference，Katholieke University，Leuven，Belgium，2002，Volume IV:1741-47．

［7］ Jalali H，Hedayati A，Ahmadian H．Modeling mechanical interfaces experiencing micro-slip/slap［J］．Inverse Problems in Science and Engineering，2011，19(6):751-764．

［8］ Iranzad M，Ahmadian H．Identification of nonlinear bolted lap joint models［J］．Computers and Structures，2012(4):96-97．

［9］ 金峰，邵伟，张立翔，等．模拟软弱夹层动力特性的薄层单元及其工程应用［J］．工程力学，2002，19(2):36-40．

［10］ 黄耀英，吴中如，王德信．薄层单元基本假设和简化探讨［J］．力学与实践，2008，130(2):49-52．

［11］ Tian H，Li B，Liu H，et al．A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools［J］．International Journal of Machine Tools＆ Manufacture，2011，51(3):239-249．

［12］ 黄开放，金建新．基于虚拟材料方法的螺栓预紧力的研究［J］．机械设计与制造，2012(8):148-150．

［13］ Mayer M，Gaul L．Segment-to-segment contact elements for modeling joint interfaces in finite element analysis［J］．Mechanical Systems and Signal Processing，2007，21(2):724-734．

［14］ 费庆国，张令弥，郭勤涛．GARTEUR有限元模型修正与确认研究［J］．航空学报，2004，25(4):372-375．