利用MSE-法求Whitham-Broer-Kaup方程组的行波解

董长紫

(陇东学院 数学与统计学院，甘肃 庆阳 745000)

0 引言

物理学中的很多现象都可以用非线性发展方程来描述.在研究非线性物理现象中，求其精确解是一项十分重要的任务.为了寻求非线性发展方程(组)的精确解,已提出了一些行之有效的方法,例如,反散射方法[1],Darboux变换法[2],齐次平衡法[3-5],广义函数法[6-7],混合指数法[8-9]，李群方法[10]等大量的求解方法.2010年Jawad AJM等在文献[11-12]中，利用修正的简单方程的方法(简称MSE)去构造非线性发展方程的行波解，得到了比较理想的结果，并且省去了之前在求精确解中的一些复杂的计算过程.本文主要利用这一简单有效的方法对于文献[13]中提到Whitham-Broer-Kaup-方程组的行波解进行计算.

1 方法简述

下面，我们列出这个方法的基本步骤：

第一步：对于给出的偏微分方程组：

(1)

利用行波变换：

u(x,y,t)=u(ζ)，v(x,y,t)=v(ζ)，ζ=x-λt+c0

(2)

把(2)代入(1)，转化为关于ζ的常微分方程组：

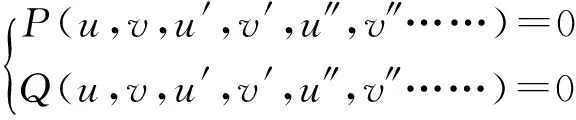
(3)

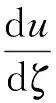
第二步：根据孤立子解理论，不妨假设u(ζ)，v(ζ)有以下的形式:

(4)

其中m0，…mi，n0…ni均为待定常数，φ(ζ)，φ(ζ)为连续可微函数.

指数M，N的值则可以通过齐次平衡法平衡方程(3)中的最高次非线性项和最高次的偏微分项的次数而确定，即

(1)如果N，M是一个正整数到第三步；

(2)如果N，M是一个分数或负整数，做变换u(ζ)=U(ζ)M,v(ζ)=V(ζ)N，再到第一步.

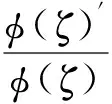
第四步：将mi,ni(i=0,1,2,……)的值和φ(ζ)与φ(ζ)代入(4)式，可得方程(1)的行波解.

注：如果方程没有这类形式的行波解，则需考虑其它的方法.

2 主要结果

首先，对给定的Whitham-Broer-Kaup方程组：

(5)

其中α，β为常数.

做行波变换：

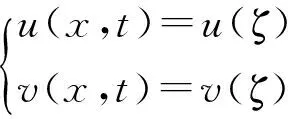
(6)

其中ζ=x-λt+c0

将(6)式代入(5)式可的结果：

(7)

由(7)式的一式可得：

H′=λu′-uu′-βu″

(8)

(8)式两边关于ζ积分，且取积分常数为零可得：

(9)

将(8)(9)代入(7)的二式可得：

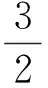
(10)

若(10)式两边关于ζ积分，且取积分常数为零可得：

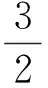
(11)

利用齐次平衡法平衡(11)式中u3的次数与u″的阶数可得M=1.

根据MSE-法设：

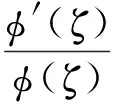
(12)

则：

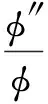
(13)

将(12)(13)代入(11)，并令φ-i(ζ)，(i=0，1，2，3，4)的系数为零可得：

(14)

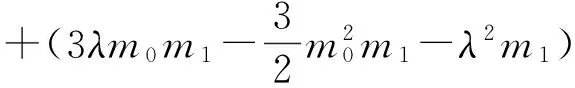
(15)

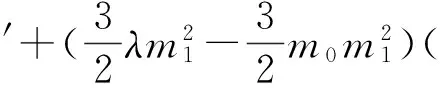
(16)

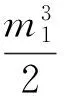
(17)

根据(15)(16)可得：

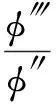
(18)

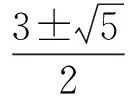
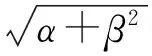
由(18)可得：

(19)

其中C1，C2为积分常数.

根据(12)(9)可得可得方程组(5)的行波解：

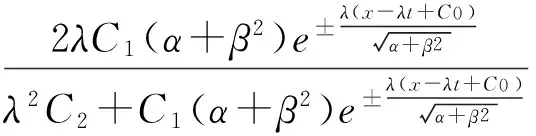
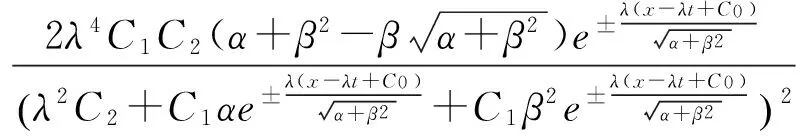
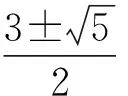
由(18)可得：

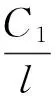
(20)

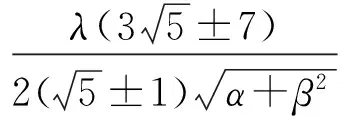
根据(12)(9)可得方程组(5)的行波解：

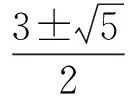
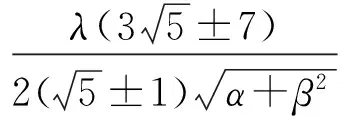
文献[13]在解的假设过程中，根据函数满足Riccati方程的条件而得到方程的解，且整个计算过程非常复杂，需要借助于一些符号计算的软件才能完成.更为重要的是，本文得到的结果在形式上比之前的结果更一般.

3 结论

利用MSE-法求非线性方程的行波解的关键是在构造行波解的时候，对于假设的函数提前未作定义，而tanh函数法、双曲函数法等均是对于给出的函数提前定义或满足一定的约束条件.因此利用这中求非线性方程行波解的方法比之前的方法更为直接、有效，且整个计算过程比较简单，无需一些复杂的计算软件.但是对于一些方程如果没有这类形式的解，则需重新考虑其它的方法.

[1]谷超豪.孤子理论及其应用[M].杭州:浙江科学技术出版社,1990.

[2]谷超豪.孤子理论中的 Darboux 变换及其几何应用[M].上海:上海科学技术出版社,1999.

[3]WANG Ming-liang.The solitary wave solutions for variant Boussinesq equations[J].Phys.Lett.A,1995,199:167～172.

[4]WANG Ming-liang.Exact solutions for a compound KdV-Burgers equation[J].Phys.Lett.A,1996,213:279～287.

[5]范恩贵,张鸿庆.非线性波动方程的孤波解[J].物理学报,1997,46:1254～1257.

[6]FAN En-gui.Extended tanh-function method and its application to nonlinear equations[J].Phys.Lett A,2000,277:212～218.

[7]FAN En-gui.Soliton solutions for a generalized Hirot a Satsuma coupled KdV equation and a coupled mKdV equation[J].Phys.Lett.A,2001,282:18～22.

[8]徐桂琼,李志斌.构造非线性发展方程孤波解的混合指数方法[J].物理学报,2002,51:946～950.

[9]徐桂琼,李志斌.扩展的混合指数方法及其应用[J].物理学报,2002,51:1 424～1 427.

[10]郭美玉,高 洁.耦合KdV 方程组的对称及精确解[J].聊城大学学报(自然科学版),2008,21:28～31.

[11]Jawad AJM,Petkovic MD,Biswas A.Modified simplify equation method for nonlinear evolution equations[J].Appl Math Comput，2010，217:869～877．

[12]Zayed EME.A note on the modified simplify equation method applied to Sharma-Tasso-Olver equation[J].Appl Math Comput，2011，218:3962～3964.

[13]ZhenYa Yan,Hongqing Zhang.New explicit solitary wane solutions and periodic wave solutions for Whitham-Broer-Kaup equation in shallow wate[J].Physics Letters A，2001，285:355～362.