若干量子幺正算符的构造及其应用

王 磊

(菏泽学院 物理系，山东 菏泽 274015)

0 引言

根据量子力学基本原理，微观粒子的状态常用态矢量(波函数)描述，而描述量子态的波函数在不同的表象中通常具有不同的表示形式，这些不同表示之间或者不同表象之间的变换称为幺正变换，其对应的算符称为幺正算符，并满足基本的幺正条件：UU+=1．由于幺正变换仅仅是数学形式上的变换，并不改变问题的物理实质，而且通过变换可以使量子力学中的许多问题大为简化并得到很好的解决，这也使得幺正变换和幺正算符在量子力学中的作用显得尤为重要[1-4]．此外，在经典物理学中也存在许多变换，如平移变换、空间反演、压缩变换、经典正则变换等，这些变换使得我们在处理许多复杂的物理学问题时显得非常便捷和有效．既然经典物理是量子物理的极限近似，那么经典变换与量子幺正变换之间必然存在一定的联系．如何找到与这些经典变换对应的量子算符映射，从而使经典变换到量子幺正变换之间的过渡能够顺利的实现，无疑是一个非常有意义的研究课题．

近年来，不对称积分被广泛研究[5-7]，本文基于动量本征矢和坐标本征矢在Fock表象中的表示，通过构造不对称积分，引入了一系列与经典变换对应的量子幺正算符，根据表象的正交完备性条件证明了其幺正性及变换特性，最后利用所构造的量子幺正算符精确求解了坐标—动量耦合谐振子的动力学问题．

1 坐标本征矢和动量本征矢在Fock表象中的表示

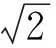
(1)

两者均满足表象的正交完备性条件：

(2)

2 对应于经典变换的若干量子幺正算符

2.1 宇称算符

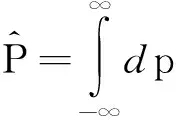
(3)

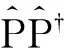
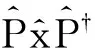
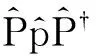
(4)

容易证明

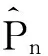
2.2 平移算符

基于经典平移变换p→p-p0，构造如下不对称积分型投影算符

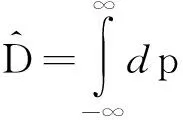
(5)

于是

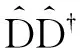
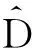
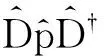
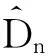
(6)

2.3 压缩算符

基于经典标度变换p→kp，利用动量本征矢构造如下不对称积分

(7)

由此得到

2.4 与经典坐标—动量变换对应的量子幺正算符

分析力学中，如果通过广义坐标和广义动量之间的变换，能够找到新的哈密顿函数，使哈密顿正则方程的形式保持不变，这种变换就叫正则变换[9]．基于经典正则变换(x,p)→(Ax+Bp,Cx+Dp)，构造如下不对称积分型投影算符

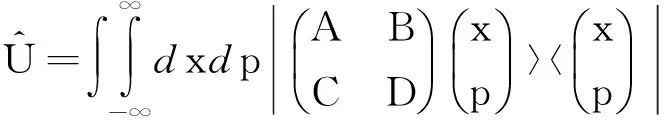
(8)

于是

令x″=Ax+Bp,p″=Cx+Dp,则

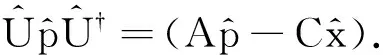
3 精确求解坐标—动量耦合谐振子的能量本征值

耦合谐振子问题在量子力学、量子光学和固体物理等多个领域均有广泛应用[10-12]，解决此类问题的关键是如何消除耦合项．作为(8)式算符U的一个简单应用，讨论一下具有坐标—动量耦合的谐振子问题，已知其哈密顿量为

(9)

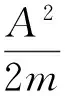
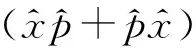
解之得一组解A=1，B=0，C=2mλ,D=1选取符合条件的幺正算符为

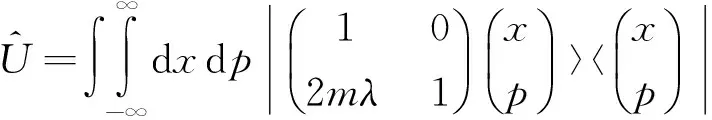
(10)

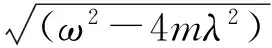
(11)

4 结论

根据坐标本征矢和动量本征矢在Fock空间中的表示，通过构造不对称积分，引入了一系列与若干经典变换对应的量子幺正算符，如宇称算符、平移算符、压缩算符以及与经典坐标—动量变换所对应的算符．利用表象的正交完备性关系，证明了这些量子力学算符的幺正性及变换特性，利用这些性质精确求解了坐标—动量耦合谐振子的能量本征值．需要指出，这些量子力学算符的显式表达式均可通过IWOP技术(有序算符内的积分技术)积分求得[14]，但本文更注重这些算符的性质及应用而非形式，因而并未进行具体的积分．

[1]查新未.四粒子任意态的概率隐形传态的两种方案[J].量子电子学报,2008,25(2):186～190.

[2]宁 丹,刘成友,于学刚，等.一类双曲型Dirac算符及幺正变换[J].吉林大学学报(理学版),2009,47(3):575～578.

[3]蒋继建,徐世民,徐兴磊.双模积分型投影算符及其应用[J].大学物理,2009,28(4):11～13.

[4]刘红艳,刘强春.利用幺正算符求解耦合谐振子和RLC量子化电路的哈密顿量[J].吉林师范大学学报(自然科学版), 2010,31(2):86～89.

[5]李体俊.坐标算符本征矢的表示与不对称投影算符的积分[J].物理学报,2008,57(7):3969～3972.

[6]王保松,张丙云.量子力学中的傅立叶变换算符[J].吉林师范大学学报(自然科学版),2010,31(1):83～85.

[7]徐世民,徐兴磊,李洪奇，等.双模坐标—动量积分型投影算符及其在量子光学中的应用[J].物理学报,2009,58(4):2174～2178.

[8]范洪义.量子力学表象与变换论[M].上海:上海科学技术出版社,1997．

[9]周衍柏.理论力学教程(第2版)[M].北京:高等教育出版社,2006.

[10]张 仲,周 波,王培吉，等.各向异性n维耦合谐振子能量本征值的代数解法[J].量子电子学报,2009,26(4):405～412.

[11]王 帅,徐世民,李洪奇.求解三模耦合谐振子精确能谱的一种方[J].大学物理,2010,29(1):36～38.

[12]厉江帆,黄春佳,姜宗福，等.含时耦合谐振子系统的时间演化与双模压缩态[J].物理学报,2005,54(2):522～529.

[13]曾谨言.量子力学导论(第2版)[M].北京:北京大学出版社,1998.

[14]范洪义.从量子力学到量子光学[M].上海:上海交通大学出版社,2001.