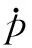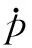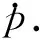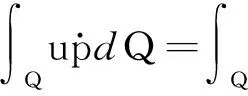一类非线性周期种群系统最优收获控制的必要条件
2014-01-15朱宏,李晗,付军*
朱 宏,李 晗,付 军*
(1.吉林师范大学 计算机学院,吉林 四平 136000;2.吉林师范大学 数学学院,吉林 四平 136000)
1 问题的提出
种群系统的最优控制问题一直被生物数学工作者所关注[1-10].文[1-4]分别研究了加权种群系统和周期种群系统的有关控制问题;文[5-6]分别讨论了种群扩散系统的边界控制与分布控制;文[7-9]分别讨论了非线性种群系统的解及其边界控制;文[10]证明了一类非线性周期种群系统最优收获控制的存在性.本文继文[10]讨论控制为最优的必要条件和确定最优控制的最优性组.具体研究如下系统(S):

(1.1)

(1.2)
p(a,t)=p(a,t+T),(a,t)∈Q,
(1.3)
p(a,0)=p0(a),a∈(0,A),
(1.4)

(1.5)
其中p(a,t)为t时刻年龄为a的单种群年龄密度分布函数;N(t)为t时刻的种群个体总数;μ(a,t;N)为平均死亡率;β(a,t;N)为平均出生率;f(a,t)为外界向种群生存环境的迁入率;v(a,t)为种群的收获率,是系统(S)的控制量;A为种群个体最高存活年龄,0 在周期环境下,研究控制问题: (1.6) 其中 (1.7) 允许控制集 U={v∈L∞(Q),0≤v(a,t)=v(a,t+T)≤L,∀(a,t)∈Q}. (1.8) 假定下列条件成立: 我们得到了最优收获控制的存在性定理: 定理1.1[10]设p(v)∈L∞(R+;L1(0,A))为问题(1.1)-(1.5)所支配的系统(S)的状态,允许控制集U由(1.8)给出,性能指标泛函J(v)由(1.7)给出,则在U中存在一个最优控制u,使得 本节讨论u∈U为系统(S)的最优收获控制的必要条件及确定最优控制的最优性组.记uλ=u+λ(v-u),0<λ<1, (2.1) (2.2) 现在证明收获控制u∈U为最优的必要条件. 定理2.1设u∈U是系统(S)关于指标泛函问题(1.7)的最优收获控制,则u∈U满足不等式: (2.3) 即u∈U为系统(S)的最优收获控制的必要条件是u满足不等式(2.3). 证明由性能指标泛函J(v)的结构(1.7)和u∈U为最优收获控制,有 0 ≤J(u)-J(uλ) 上式两边除以λ>0,令λ→0+取极限得 (2.3) 下面我们导出确定最优控制u∈U的最优性组.为了变换不等式(2.3),定义伴随状态q(a,t;v)=q(v): (2.4) 上述问题(2.4) 容许唯一解q(u)∈L∞(R+;L1(0,A)).由下面的定理给出. 定理2.2假设定理1.1的条件成立.设u∈U是系统(S)的最优控制,p(u)∈L∞(R+;L1(0,A))是问题(1.1)-(1.5)的广义解,则伴随问题(2.4)容许唯一的广义解q(u)∈L∞(R+;L1(0,A)). (2.5) 综上所述,我们得到本文的主要结果. 定理2.3设p(u)∈L∞(R+;L1(0,A))是系统(S)即问题(1.1)-(1.5)的解,性能指标由式(1.7)给出定义,容许控制集合U由(1.8)式确定,若u∈U为系统(S)关于式(1.7)的最优控制,则u∈U由方程(1.1)-(1.5)(其中v=u)及伴随方程(2.4)和变分不等式(2.6)所构成的最优性组的联立解{u,p,q}确定. [1]Barbu V,Iannelli M.Optimal Control of Population Dynamics [J].Journal of Optimization Theory and Applications,1999,102(1):1~14. [2]雒志学,王绵森.具有年龄结构的线性周期种群动力系统的最优收获控制问题.数学物理学报.2005,25A(6):905~912. [3]叶山西,赵 春.一类具有年龄分布和加权的种群系统的最优控制[J].应用数学,2007,20(3):562~567. [4]何泽荣,王绵森.一类非线性周期种群系统的最优控制.应用数学2003,16(3):88~93. [5]陈任昭,张丹松,李健全.具有空间扩散的种群系统解的存在唯一性与边界控制[J].系统科学与数学,2002,22(1):1~13. [6]李健全,朱 宏,付军.具空间扩散的时变种群系统的最优分布控制. 吉林师大学报(自然科学版),2005,27(1):6~8. [7]吴秀兰,付 军.一类半线性种群系统广义解的存在唯一性. 吉林师大学报(自然科学版),2007,29(1):60~62. [8]付 军,艾 红. 一类非线性种群系统的解[J]. 吉林师范大学学报(自然科学版), 2013, 34(2): 59~61. [9]付 军, 朱 宏. 具年龄和加权的半线性种群系统的最优边界控制[J]. 吉林大学学报(理科版),2013, 51(1): 27~33. [10]付 军,吴 喆,朱 宏.一类非线性周期种群系统的最优收获控制.东北师大学报(自然科学版),2013,45(2):5~9. [11]博格M S.非线性与泛函分析[M].(余庆余译).北京:人民教育出版社,1989.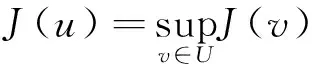

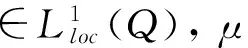
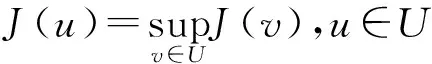
2 主要结论