两类图的序列性

吴罗义

(武夷学院 数学与计算机学院,福建 武夷山 354300)

0 引言

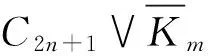
定义：对于序列图G的某一序列值，如果存在整数k，使得每条边uv∈E(G)有

f(u)≤k,f(v)>k或者f(u)>k,f(v)≤k

则称这种序列标号为序列平衡标号，称为此种标号的特征.

1 引理

引理1[6]：若q条边树T有序列平衡标号f，特征为k，且f(vi)=0,f(vj)=k+1，f(vk)=k,f(vl)=q,则vivj∈E(T)且为边标号最小的边，vkvl∈E(T)且为边标号最大的边．

证显然f：V(T)→{0,1,2,…，q}为单射，

因为φ是T的序列平衡标号，所以φ(vi)+φ(vj)为连续的不同的整数片段

当vivj∈E(T)时，由f导出的边标号f′满足

f′(vivj)=f(vi)+f(vj)=q+2k+1-(φ(vi)+φ(vj))

所以，f(vi)+f(vj)为连续的不同的整数片段.

根据f的标号情况，显然对应的特征为k.

引理3[5](一般图标号)：φ是G的序列标号当且仅当f=m-φ是G的序列标号.其中f(u)=(m-φ)(u)=m-φ(u),u∈V(G)

推论1：若φ是q边树T的序列平衡标号，对应的特征为k，则f=q-φ也是T的序列平衡标号，且特征为q-k-1.

2 主要定理

定理1若T1，T2分别具有某两个序列平衡标号f1,f2的树，边数分别为q1,q2，对应的特征分别为k1,k2，那么将T1中标号为0，k1,k1+1,q1的任意顶点与T2中标号为0，k2,k2+1,q2的任意顶点粘接，所得的树T*为具有序列平衡标号的序列树．

证根据引理2和推论1可知：存在由fi导出的新标号，使得Ti在fi下标号为0，ki,ki+1,qi的顶点在导出的新标号下对应为0，且导出的新标号也是序列平衡标号．所以要证明命题成立，只需证：“T1中标号为q1的顶点与T2中标号为0的顶点粘接所得的树T*为具有序列平衡标号的序列树．”成立即可.

Ti可划分为Xi={x∈V|f(x)≤ki}和Yi={x∈V|f(x)>ki}．

定义T*的顶点标号φ：

树T*的边为q1+q2，顶点为q1+q2+1.

易验证，φ为V(T)→{0,1,2,…，q1+q2}的单射.

下面证明由φ导出的T*边标号为q1+q2个连续的不同的整数.

因为f1是T1的序列平衡标号，特征为k1，结合引理1，可得T1的q1条边在f1导出的边标号为q1个连续不同整数{k1+1,k1+2,…,q1+k1}；同理可得T2的q2条边在f2导出的边标号为q2个连续不同整数{k2+1，k2+2，…，q2+k2}.

xy∈T1(x∈X1,y∈Y1)，则由φ导出的边标号φ(x)+φ(y)=f1(x)+f1(y)+q2-k2，所以T1的q1条边在φ导出的边标号为q1个连续不同整数{q2+k1-k2+1,q2+k1-k2+2,…，q1+q2+k1-k2}；

xy∈T2(x∈X2,y∈Y2)，则由φ导出的边标号为φ(x)+φ(y)=f2(x)+f2(y)+q1+q2+k1-2k2，所以T2的q2条边在φ导出的边标号为q2个连续不同整数{q1+q2+k1-k2+1,q1+q2+k1-k2+2,…，q1+2q2+k1-k2}；

所以，φ导出T*的边标号为q1+q2个连续的不同的整数

{q2+k1-k2+1,q2+k1-k2+2,…，q1+2q2+k1-k2}

所以，φ是T*的序列标号，取k=q2+k1-k2，由粘接方式，可把T二部划分为：

X={x∈X1∪Y2|φ(x)≤q2+k1-k2}或Y={x∈X2∪Y1|φ(x)>q2+k1-k2}.

综上定理成立．

定理2若T1，T2分别具有某两个序列平衡标号f1,f2的树，边数分别为q1,q2，对应的特征分别为k1,k2，那么将T1中标号为0，k1,k1+1,q1的顶点与T2中标号为0，k2,k2+1,q2的顶点用一新边连接起来，所得的树T*为具有序列平衡标号的序列树．

证根据定理1证明分析，只需证：“T1中标号为q1的任意顶点与T2中标号为0的任意顶点用一新边连接起来所得的树T*为具有序列平衡标号的序列树．” 成立即可.

构造所得的树T*边数为q1+q2+1，顶点为q1+q2+2.

Ti(i=1,2)可划分为Xi={x∈Vi|fi(x)≤ki}和Yi={x∈Vi|fi(x)>ki}.

定义T的顶点标号φ

从φ的标号方式可知，最大的顶点标号为q1+q2+1并且各点标号不同，所以φ为V(T)→{0，1，…，q1+q2+1}的单射.

下面证明φ导出的T*边标号为q1+q2个连续的不同的整数.

仿照定理1证明可知T1的q1条边在φ导出的边标号为q1个连续不同整数{k1+k2+2,k1+k2+3,…，q1+k1+k2+1}；T2的q2条边在φ导出的边标号为q2个连续不同整数{q1+k1+k2+3,q1+k1+k2+4,…，q1+q2+k1+k2+2}.

根据连接方式可知新增加的边标号为q1+k1+k2+2，

所以，φ导出T*的边标号为q1+q2+1个连续的不同的整数

{k1+k2+2,k1+k2+3,…，q1+q2+k1+k2+2}.

所以，φ是Τ*的序列标号，取k=k1+k2+1，由粘接方式，可把T二部划分为：

X={x∈X1∪Y2|φ(x)≤k}或Y={x∈X2∪Y1|φ(x)>k}.

综上定理成立．

注：由定理1与定理2所生成的序列树仍是序列平衡树的，所以可以推广到n棵序列平衡树“连接”或“粘接”的情形.

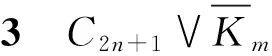
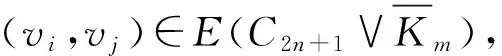
根据标号可知C2n+1中的边标号为连续整数片段{n,n+1,…，3n}；

每个ki(i=2n+1,2n+2,…，2n+m)与ci(i=0，1，…，2n)各点连接的边共2n+1条，这2n+1条边标号为

{3n+(j-1)·2n+j,3n+(j-1)·2n+j+1,…，3n+(j-1)·2n+j+2n},j=1,2,…，m

为连续整数片段.所以与ki邻接的边标号为连续整数片段{3n+1,3n+2，…，3n+2mn+m}.

综上所述：则由φ导出的边标号连续整数片段{n,n+1,…3n,3n+1,…，3n+2mn+m}.

例：具有图1序列标号的两棵树T1,T2，将T1标号为最大的顶点与T2标号为最大的顶点粘接可得图2的序列标号；将T1标号为最大的顶点与T2标号为最大的顶点粘接联接可得图3的序列标号.

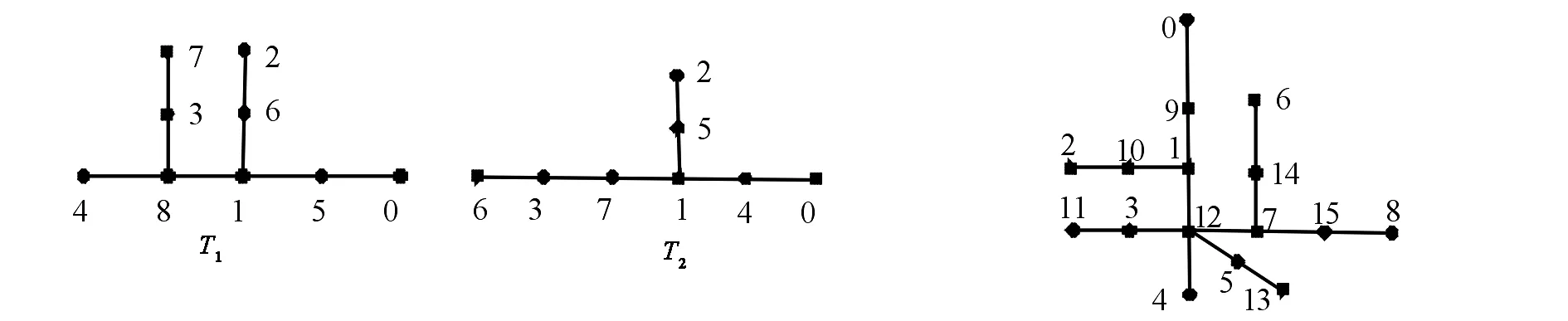
图1T1、T2树的序列标号图2T1与T2粘接的序列标号

[1] J.A.Gallian.A Dynamic Survey of Graph Labeling[J]．Electronic Journal of Combinatorics，2002，5：41～42．

[2]D.Jungreis and M.Reid，Labeling grids[J].Ars Combin.， 1992,34:167～182．

[3]马克杰．优美图[M]．北京：北京大学出版社，1991．

[4]贺 丹，刘彦佩．树积序列性及序列标号[J]．北方交通大学学报，2003，27(3)：46～49．

[5]朱振广，徐美进，刘春峰．序列图的一些必要条件与非序列图类[J].辽宁工程技术大学学报，2007,26(2)：318～320．

[6]吴罗义，朱振广，阚永志.一类序列树的构造[J].辽宁工业大学学报，2009,29(4)：268～271.

[7]M.Z.Youssef.Two general results on harmonious labelings[J].Ars Combin.，2003,(68)：225～230.

[8]张克民.某些图论问题的进展[J].数学研究与评论，2007,7(3):563～575.

[9]王湘平.图K4×C2的临界群[J].吉林师范大学学报(自然科学版),2009,30(2):53～59.

[10]丁孝全.一类图的序列标号[J].信阳师范学院学报,2007,13(3):251～253.