基于PR控制器的APF电流跟踪控制策略研究

祝 慧，周 苗，席自强

（湖北工业大学电气与电子工程学院，湖北 武汉430068）

补偿电流跟踪控制部分是有源电力滤波器（APF）的核心，其性能直接影响到谐波补偿的效果［1－2］。常用的补偿电流跟踪控制方式是通过坐标变换将三相静止坐标系中的电压、电流变成以各次谐波角速度旋转的dq坐标系下，利用简单的PI控制器实现电流的无静差控制，同时也可实现有功、无功的解耦控制。但是当变流器采用PI调节器控制时，输出电压存在相位差和幅值差［3－4］。根据谐振控制器对于特定频率正弦信号具有无限大增益的特点［5－6］，本文采用比例谐振（Proprotional Resonant，PR）调节器来得到更优良的输出特性，改善有源滤波器的谐波抑制效果。

1 同步谐波旋转坐标系下电流环控制

当APF需要补偿特定的n次谐波时，若以待补偿谐波同步旋转的dqn轴为参照，补偿电流在旋转坐标系下的分量idn、iqn将变为直流量，其数学模型为

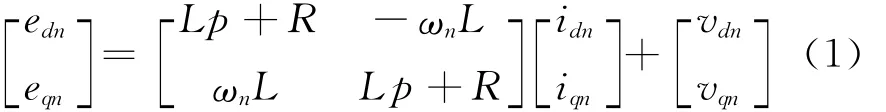
式中：vdn、vqn为dqn坐标系下的APF交流侧电压；ωn为n次谐波角频率；edn、eqn为dqn坐标系下的系统电压。

从式（1）可以看出dqn轴电流中存在着耦合现象，可采用坐标变换的方式，将不同的耦合量由对应的dqn坐标系转移到dq坐标系，得到

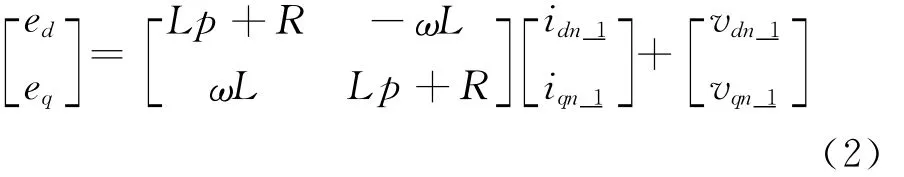
在dqn坐标系中，APF电流环的控制在本质上是实现idn、iqn跟踪上一个指定的直流分量，而这个指定分量的大小则为对应次数待补偿谐波的幅值。对于dqn坐标系，式（2）可变换为：

从式（3）和式（4）可以看出，传统的PI调节器便可以实现idn、iqn直流信号的无静差跟踪。以d轴为例，不考虑轴间耦合影响以及系统电压的扰动，PI控制器以零极点形式表示，即KiIn＝KiPn／τis。其等效开环控制传递函数

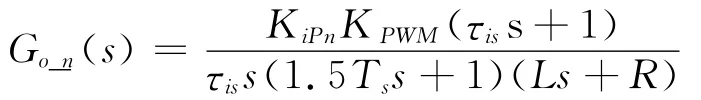
在考虑该PI调节器稳态误差以及动态响应特性，采用零极点抵消法对该典型二阶控制系统进行等效降阶，即τis＝L／R。降阶后的电流内环开环传递函数

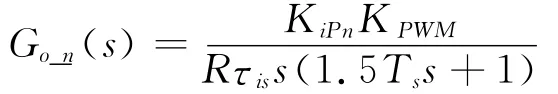
2 基于PR控制器的静止坐标系电流环控制

基于PR控制器的静止坐标系电流环控制与同步谐波旋转坐标系电流环控制之间最大的差异是电流环所处的坐标系。后者的控制结构处于对应次谐波频率的dqn坐标系中，其控制量为直流量，因此能够达到较高的跟踪精度，但是同时需要进行大量的矩阵计算并设计多个独立的PI控制器。静止坐标系电流环控制的控制对象和控制过程在αβ坐标系中进行，对应的控制量为时变的交流信号，因此需要对控制器作相应的改进处理。一种可行的方法便是将dqn坐标系下的控制器传递函数变换到αβ坐标系下，其实现过程如下：

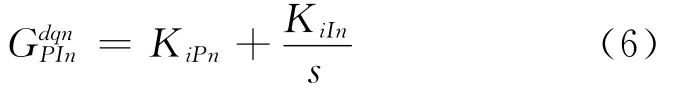
将式（6）代入式（5）中可得：

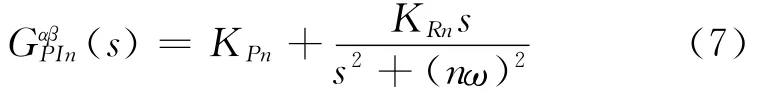
指定次谐波控制器在αβ坐标系中的表现形式如式（7）所示，这种控制器也称为比例谐振控制器，即PR控制器。其中式（7）右边的第二项具有广义积分的特性，在角频率nω处增益为无穷大，而在其它频率处增益很小，即能够实现与其同频正弦信号的无静差跟踪，达到指定次谐波补偿控制的调节作用。因此，在静止αβ坐标系中利用PR控制器可以减少大量的坐标变换过程，无需较大的控制增益便可实现高频正弦信号的无静差跟踪。

然而这种PR控制器也具有一定的局限性，由式（7）所示，PR控制的谐振频率需要与电网中的谐波频率一致。为了提高控制性能的稳定性以及数字化实现，有学者对常规PR控制进行改进设计，使其在电网环境瞬态变化时，依然能够保持对指定次谐波的高增益控制特性，同时也拥有较强的频率鲁棒性。令ωn＝nω，其控制传递函数

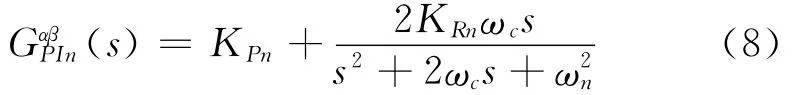
与式（7）不同，式（8）在谐振频率处的增益有限，但系统仍然具有相对优异的稳态误差特性。其中比例参数KPn会影响控制系统的稳定性，若选取得太大，一方面对应控制器频段的增益会变大，另一方面会导致控制系统的幅值裕度变小；若选取得太小，会造成系统抗干扰能力变差。控制系统谐振频率处的带宽可以通过ωc参数来改变，有助于提高控制器对系统频率变化的鲁棒性。

将s＝jω代入式（8），根据对带宽的定义，控制器应满足

此时，计算得到的两频率之差即为带宽，令ωc参数的约束条件为

通过式（9）与式（10）计算可得，谐振控制器的带宽为ωc／π。

图1、图2所示的波形即为式（7）得到的常规PR控制器幅相频特性曲线。以谐振频率为5次谐波频率为例（图1），当频率为250Hz时，其具有最大控制增益。如欲对指定次谐波（如5、7、11、13等次谐波）进行补偿时，其对应的幅频特性曲线见图2。虽然这种形式具有较好的理论指定次控制效果，但是当电网频率波动时，其控制增益会有极大的变化。

图1 谐振控制器伯德图（5次）

图2 指定次谐振控制器幅频图

图3 、图4为参数改变时改进型PR控制器的幅相频特性曲线。当保持ωc不变时，逐渐增加KRn的大小，控制器的增益也随之增加，但相位带宽并没有太大变化。当保持KRn不变时，逐渐增加ωc的大小，控制器的增益随之增加，同时相位带宽也会增加。

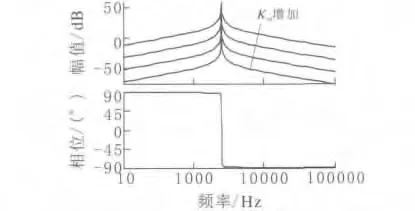
图3 KRn改变时的伯德图

图4 ωc改变时的伯德图

静止坐标系下电流环控制框图见图5，将系统负载侧电流iLa、iLb、iLc送入谐波检测算法中分离出指定次谐波变量。在这个环节中，由于静止坐标系电流环的指定频次控制特性，该谐波检测算法是可选的。若检测环路中没有谐波检测环节，只需要针对指定次谐波进行PR控制器设计也可以达到指定次谐波补偿控制的目的，但是这种情况下对PR控制器的参数要求比较高，需要防止不同次数谐波之间的混合干扰影响；若检测环路中有谐波检测环节，则上述混合干扰环节会明显减少，但同时其控制性能会受到谐波检测算法中低通滤波器的约束。将负载侧谐波检测信号与补偿信号的差送入PR控制器中，该调控过程在αβ坐标系下完成，不仅省去了大量的坐标变换单元，同时也省去了解耦步骤。其控制结果直接作为指令电压信号送入SVPWM模块中进行PWM波形的调制，作用于有源电力滤波器六路开关器件进行谐波跟踪控制。

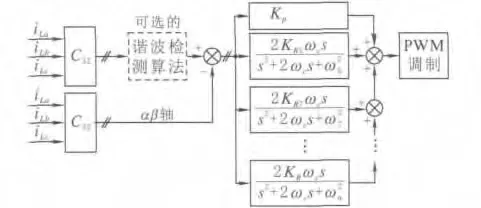
图5 静止坐标系下电流环控制框图

3 仿真实验研究

为了验证基于PR控制器的补偿电流控制算法的有效性，针对该算法做仿真与实验研究。其中仿真环境为：1）电源，380V／50Hz；2）负载，整流桥带阻感性负载，其中R＝2Ω，L＝1mH；3）电源进线电感，100μH；4）APF输出电感，1.5mH；5）APF直流侧电压，850V。

图6、图7为补偿前后电流的仿真波形，图8、图9为补偿前后电流的实验波形。该波形显示，基于PR控制器的补偿电流控制策略能够极大的抑制谐波对电网侧的影响。

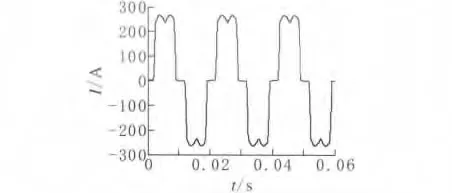
图6 负载侧电流仿真波形

图7 补偿后源侧电流仿真波形

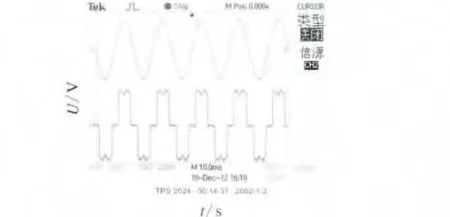
图8 负载侧电流实验波形图

图9 补偿后源侧电流实测波形

4 结论

在同步谐波旋转坐标系下的电流环控制中，需要在特定次谐波检测环节中分离出谐波信号，其中各路谐波信号分别采用一个PI控制器。此方法可实现较高的跟踪精度以及延时补偿，但是其实现过程需要大量复杂的坐标变换和PI控制。在静止谐波旋转坐标系电流控制过程中，可以不需要谐波检测环节，在理论上仅需要进行少量的坐标变换以及PR控制，便可实现同样的控制效果。仿真结果说明：基于PR控制器的APF电流跟踪控制策略效果非常好。

［1］ Yang Y，Zhou K，Blaabjerg F.Harmonics suppression for single－phase grid－connected PV systems in different operation modes［C］.Long Beach.CA：Applied Power Electronics Conference and Exposition：APEC，2013 Twenty－Eighth Annual IEEE，IEEE，2013：889－896.

［2］ Wang J，Nademi H，Norum L.Control of input current harmonics and output voltage of three－phase voltage source PWM rectifier using Model Predictive Control［C］.Taipei：Industrial Electronics：ISIE，IEEE，2013：1－6.

［3］ 彭自强，罗 安，陈燕东.基于分频虚拟电阻的多逆变器并联控制策略［J］.电网技术，2013，37（11）：3 276－3 280.

［4］ 吕志鹏，苏 剑，李 蕊.不同功率等级微源逆变器并联控制新方法［J］.电工技术学报，2013，28（07）：191－198.

［5］ 杨秋霞，梁雄国，郭小强.准谐振控制器在有源电力滤波器中的应用［J］.电工技术学报，2009，24（07）：171－176.

［6］ 郑昕昕，肖 岚，田洋天.双向三相AC／DC变流器的无锁相环控制策略［J］.中国电机工程学报，2013，33（36）：79－87.