潜孔冲击器活塞的应力强度因子有限元分析

杨 雄，金连富，萧志钰

（长江大学机械工程学院，湖北 荆州434023）

从大量工程现场断裂事故中发现，超过60%的金属零部件的破坏与材料局部缺陷有关。这些缺陷往往在一定条件下会成为裂纹源，进而在工作的过程中不断扩展，引起断裂。由于传统的设计是以完整结构的静强度为参考依据，缺乏对不完整构件的强度估算，使得构件的寿命远远小于设计要求的寿命［1］。在实际应用中，大部分潜孔冲击器活塞沿着小径倒圆角部位断裂，根据理化实验和有限元力学的分析结果，潜孔冲击器活塞在小径倒圆角部位存在应力集中［2］，在断面处呈线弧状扩展的痕迹。因此，对含裂纹的潜孔冲击器活塞的断裂行为进行分析和对断裂参量进行评定是十分必要的。而应力强度因子是衡量裂纹尖端应力场强度的重要指标，也是判断裂纹是否失稳扩展的重要依据。

1 基于ANSYS求解应力强度因子

断裂根据结构中裂纹体的受力情况，分别为张开型（Ⅰ型）、滑开型（Ⅱ型）、撕裂型（Ⅲ型）。在工程实践中存在的诸多问题常被简化为I型处理［3］。

经过有限元软件ANSYS来计算三维裂纹尖端的应力强度因子时，主要是选用“自下而上”的方式来建立裂纹体，即由点―线―面―体的方法来进行模拟。除了微小的裂纹体以外，活塞的绝大部分是非裂纹体，把裂纹体与非裂纹体通过布尔运算的overlap（搭接），使之成为一个连续体并且有共同的边界。

首先，选择Mesh200单元对裂纹表面进行网格划分，然后，选择SOLID95奇异单元，通过扫描对整个裂纹体进行网格划分［4］。

活塞冲击钻头时，与钻头发生接触，即活塞下端表面与钻头上表面接触。选择自动单触点接触式（ASSC自动单面）。模拟活塞碰撞后反弹的全过程，设置活塞在钻头上方5mm的位置，并给活塞施加一个初速度，并设定这个速度在5mm运行期间内不变，整个分析时间取为0.001s，分析时间步长20μs［5］。建立局部坐标系时，裂纹前缘要与局部直角坐标系的X轴相垂直，裂纹面要与Y轴垂直。当执行KCALC命令时，该坐标系必须是激活的模型坐标（CSYS），并且是结果坐标系［6］。

2 求解结果及分析

2.1 裂纹处于不同位置、不同裂纹长度的应力强度因子

由于活塞内孔直径为28.6mm，外圆直径为65 mm，所以活塞厚度为裂纹内孔表面的距离，a／t分别取0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9。针对每个深度，裂纹长度分别取0.4mm、0.6mm、0.8mm、1.0mm、1.2 mm、1.4mm、1.6mm，通过 ANSYS进行运算，得出结果如表1所示。

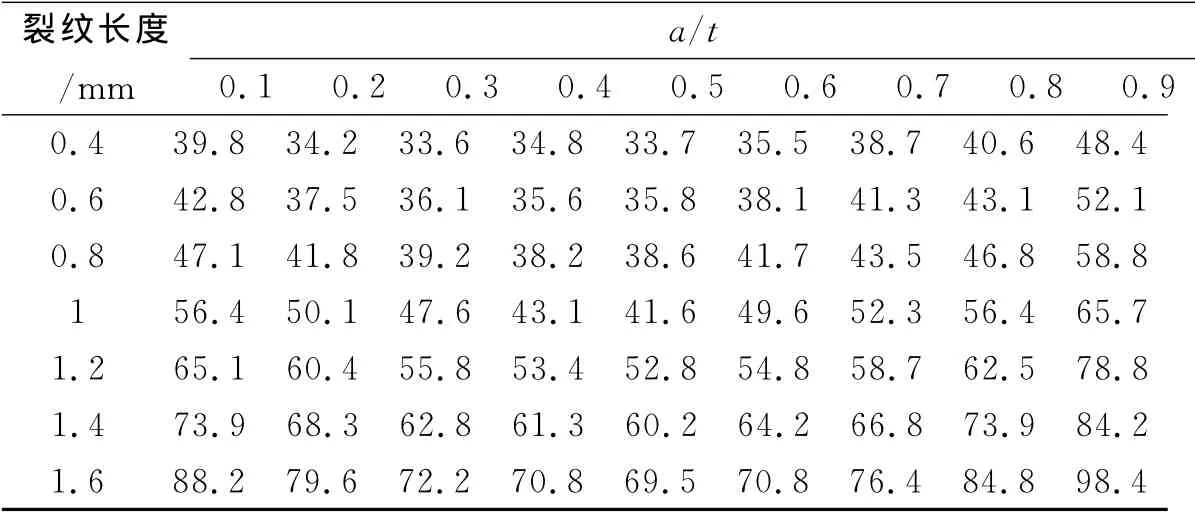
表1 不同位置裂纹长度的应力强度因子

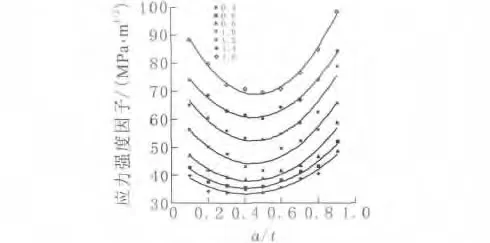
图1 不同深度长度的裂纹的应力强度因子变化曲线

从图1可知，裂纹的应力强度因子随裂纹位置与裂纹长度的变化曲线基本一致，都呈现U型的特性。当活塞长度一定，裂纹处于活塞厚度的中间位置时，应力强度因子最小，裂纹越靠近内外表面时，应力强度因子随之增大，而且靠近外表面位置比靠近内表面的裂纹应力强度因子大；当同一位置的裂纹随着裂纹长度的增加而增大，而且裂纹越长，应力强度因子增加的幅度越大。

2.2 内孔直径、倒圆角半径和冲击末速度对应力强度因子的影响

应力强度因子还与潜孔冲击器活塞的几何结构和实际工况有关［7］。在活塞的几何结构中，影响活塞壁厚的内孔直径和小径处的倒圆角半径是最为关键的因素，实际工况不同主要反映在活塞的冲击末速度上。在a／t＝0.9处，分别计算了在7～12m／s的冲击末速度下，内孔直径分别为24.6～34.6mm和倒圆角半径分别为14～16mm情况下的应力强度因子值如表2所示，分析结果见图2－4。

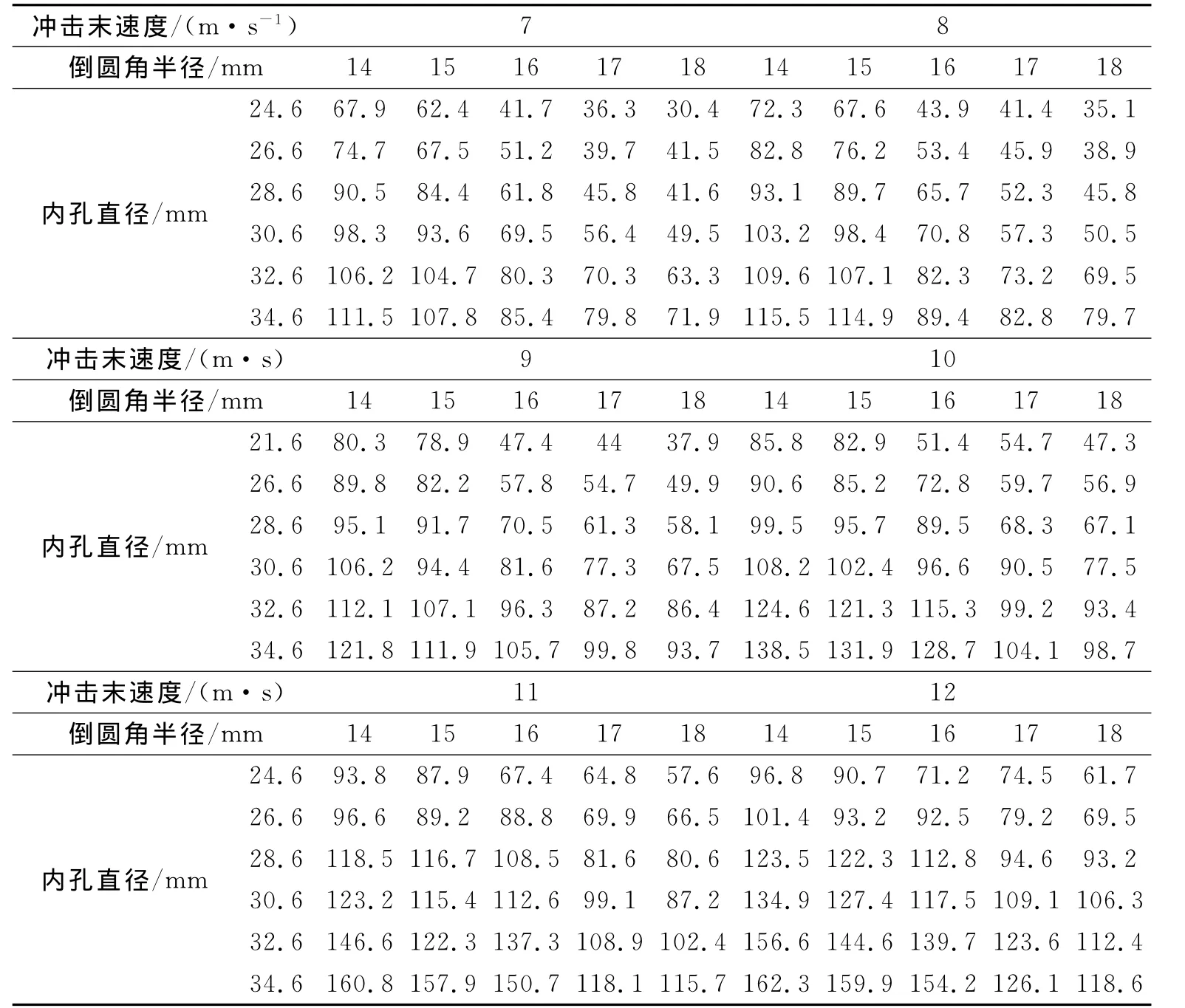
表2 不同条件下的应力强度因子值

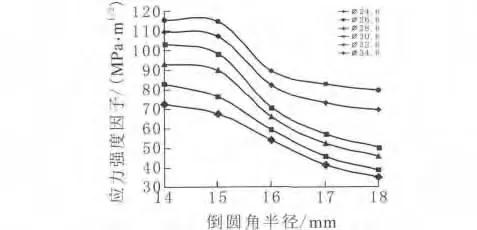
图2 应力强度因子随倒圆角半径和内孔直径的变化曲线

图3 应力强度因子随冲击末速度和内孔直径的变化曲线

由图2可见，裂纹的应力强度因子呈随着倒圆角半径的增大而减小和随着内孔直径的增大而增大的变化趋势。其中，当内孔直径不大于28.6mm时，应力强度因子在倒圆角半径15～16mm变化区间比较敏感，即倒圆角半径由16mm减小到15mm时，应力强度因子快速增大。

图3是在倒圆角半径为16mm情况下的应力强度因子随冲击末速度和内孔直径的变化曲线，其反映了应力强度因子随冲击末速度的增大而发生不同程度的增大，并且随着内孔直径的增大出现了拐点右移的现象：壁厚越小，对于冲击末速度的变化而引起的应力强度因子的变化幅度越大，并且随着壁厚的减小，引起应力强度因子快速变化的冲击末速度也逐渐减小（拐点右移）。内径分别为30.6～34.6mm，26.6～28.6mm、24.6mm，引起应力强度因子快速变化的冲击末速度为8m／s、9m／s和10m／s。

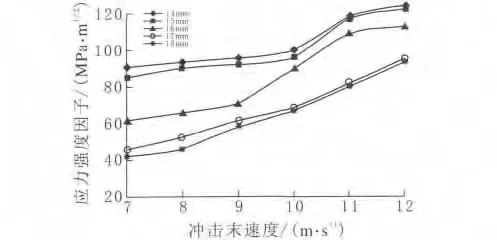
图4 应力强度因子随冲击末速度和倒圆角半径的变化曲线

由图4可知，应力强度因子随着冲击末速度的增大而增大，随着圆角半径的增大而减小。当倒圆角半径大于16mm时，其在各个冲击末速度下的应力强度因子都高于倒圆角半径为16mm时的应力强度因子，应力强度因子在冲击末速度达到10m／s后才增大24.1%；而倒圆角半径为16mm时，应力强度因子在冲击末速度达到9m／s后就急剧增大54%；当倒圆角半径大于16mm时，应力强度因子呈现现象变化趋势，而且17mm的倒圆角半径与18 mm的倒圆角半径时其应力强度因子值相当接近。

3 结论

1）裂纹处于潜孔冲击器活塞外表面时影响最大。

2）计算出在a／t＝0.9处，分别在7～12m／s的冲击末速度下，内孔直径分别为24.6～34.6mm和倒圆角半径分别为14～16mm情况下的应力强度因子。当内孔直径不大于28.6mm，倒圆角半径在15～16mm时，应力强度因子变化大；应力强度因子都随冲击末速度的增大而发生不同程度的增大，并且随着内孔直径的增大出现了拐点右移的现象。当倒圆角半径大于或等于16mm时，应力强度因子都发生较大幅度的增大。

3）措施：a）加强对外表面内部1～2mm处位置的裂纹检测；b）潜孔冲击器活塞结构优化，适当减小内孔直径至26.8mm，小径处倒圆角半径增大至17 mm为佳；c）冲击末速度控制在7m／s为宜。

［1］ 瞿伟廉，鲁丽娟，李 明.工程结构三维疲劳裂纹最大应力强度因子计算［J］.地震工程与工程振动，2007，27（06）：58－60.

［2］ 陈俊宇，徐人平，张海敏.液压冲击器活塞的非线性有限元分析 ［J］.南方金属，2009（06）：15－17.

［3］ 中国航空研究院编著.应力强度因子手册（增订版）［M］.北京：科学出版社，1993：181－205.

［4］ 石海燕.活塞疲劳失效的力学分析［D］.山东：山东理工大学，2008.

［5］ 詹 军，殷 坤，于清杨，曾建华.风动冲击器活塞冲击末速度的有限元研究 ［J］.煤田地质与勘探，2003，31（06）：58－60.

［6］ 王 锋.三维应力强度因子分析及干涉预应力影响研究 ［D］.西安：西北工业大学，2007.

［7］ 高丽稳，周志鸿.冲击机械活塞强度研究现状［J］.工程机械，2005（01）：37－49.