基于果蝇优化算法的月球车全局路径规划

毛正阳，方 群

（西北工业大学 航天学院 航天飞行动力学技术重点实验室，陕西 西安 710072）

月球车是能够在月球表面移动，实施近距离探测，从而有效拓展探测范围的航天器。月球车要适应探测环境，需要找到从起始位置到目标位置的安全路径，即进行路径规划。路径规划分为基于地图的全局路径规划和基于传感器的局部路径规划。

路径规划的算法正在不断的发展和完善中。文献[1]将人工势场的思想引入到蚁群算法中，构建并加入了权重可调的引力概率函数作为启发因子，使新的算法在较快的收敛速度下仍能得到全局较优解；文献[2]针对粒子群算法在路径规划中易造成不收敛的问题，去掉了速度更新中的速度惯性因子，同时引入经典遗传算法中的变异因子以增强算法的全局寻优能力；文献[3]以多组蚂蚁为研究对象，采用最近邻居搜索策略和趋近导向函数相互协作完成全局最优路径的搜索。

全局路径规划侧重于最短可行路径的选取，不考虑速度等因素[2]。本文讨论的是在栅格地图上进行月面巡视器的全局路径规划问题，将2011年Wen-Tsao Pan提出的果蝇优化算法改进后应用于全局路径规划，达到快速寻找到最优路径的目的。

1 果蝇优化算法

Wen-Tsao Pan从果蝇的觅食行为得到启发，提出了寻求全局优化的新方法[4]。果蝇本身在感官知觉上优于其他物种，其嗅觉器官能够很好的搜集漂浮在空气中的各种气味，甚至能嗅到40公里外的的食物源。果蝇飞近食物后亦可使用敏锐的视觉发现食物与同伴聚集的位置，并往该方向飞去，如图1所示。

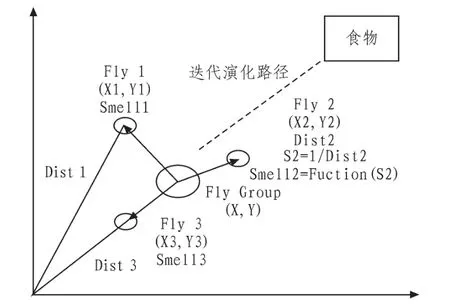
图1 果蝇群体迭代搜索食物示意图Fig.1 Food finding iterative process of a fruit fly swarm

依照果蝇搜索食物的特性，可将果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）归纳为以下几个重要步骤：

1）随机初始果蝇群体位置X，Y。

2）分配果蝇个体利用嗅觉搜寻食物随机方向与距离：

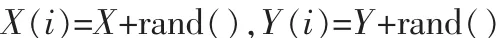
3）估计果蝇与原点的距离Dist，再计算味道浓度判定值S，S为距离Dist的倒数：

4）味道浓度判定值代入味道浓度判定函数（Fitness Function）以求出该果蝇个体位置味道浓度smell：

5）找出果蝇群体中味道浓度最大的果蝇：

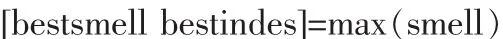
6）保留最佳味道浓度值与X、Y坐标，此时果蝇群体利用视觉往该位置飞去：

smellbest=bestsmell；

X=X（bestindex）；

Y=Y（bestindex）；

7）进入迭代寻优，重复步骤2）-5），并判断味道浓度是否优于前一迭代味道浓度，若是则进行步骤6）。

2 基于果蝇优化算法的路径导航点规划问题建模

如图2所示，将全局地图进行等栅格大小划分，I为起始点，G为目标点。果蝇以给定的速度沿栅格边飞行，图2中粗实线为飞行路径，P1、P2、P3为路径导航点，将起点 I视为P0，终点G视为P4，则整个路径长度

路径规划问题即是对Pj的位置进行优化选择，保证连线PjPj+1不与障碍物相交并使LP最小。

图2 路径导航点规划建模Fig.2 Model of the path navigation points planning

3 果蝇优化算法的改进与实现

文献[5]对果蝇优化算法做了仿真分析，分析表明果蝇算法稳定性较差，易于陷入局部最优。

由上可知，利用FOA算法进行路径规划时，需要对参数进行必要的设置，对算法做出必要的改进。考虑到FOA算法的参数设置是导致算法是否会陷入局部最优的关键，本文提出基于改进参数设置方法的改进FOA算法，其对算法的改进包括：第一，由于路径规划问题的起始点与目标点均是已知的，因而2中步骤1）果蝇群体的初始位置及食物源位置可以设为是已知的；第二，月球车具有一定的越障能力，2中步骤2）需要给予果蝇一定的越障能力并设置允许行进代价值范围；第三，一般情况下，起始点和目标点相距较远，这样2中步骤3）Dist的取值范围会很大，为此当计算味道浓度判定值S时，使得S的取值范围很小，因而将其代入味道浓度判定函数时，很可能引起早熟收敛并陷入局部最优。针对此问题，本文提出将Dist直接带入味道浓度判定函数，计算与目标点距离差。因此不需将S代入味道浓度判定函数，从而不易陷入局部最优，提高了算法的稳定性，并可使果蝇群体向已知食物源飞行。

4 仿真及分析

4.1 环境建模

月球表面总体上可以分为月海和高地两大地理单元，分布有大小不一的岩石和撞击坑。根据以往获得的月面地形信息，拟合得到其数学模型[6]。本文以平缓月海为例建立月面数字地形，综合巡视器工作能力和体积水平，确定研究区域为100 m×100 m。图3为月面数字地形图，单位m。然后分析其可通行性，得到可通行性代价地图。

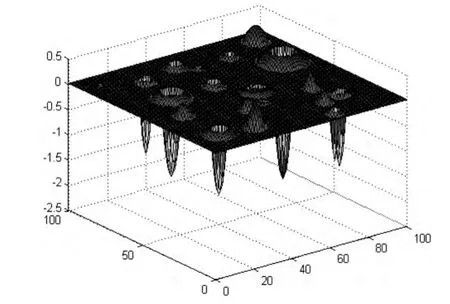
图3 月面数字地形图Fig.3 Digital terrain of lunar surface

4.2 FOA算法的路径规划

利用FOA优化算法进行仿真时，设定初始位置（1，1，0），目标点（100，100，0），种群规模 200，迭代次数 500。规划路径，结果如图4（a）所示，迭代次数如图4（b）所示。多次仿真，除少数几次外，均陷入局部最优，无法得到完整规划路径。

4.3 改进FOA算法的路径规划

利用改进FOA优化算法进行仿真时，设定初始条件与5.2相同。规划路径，结果如图5（a）所示，迭代次数如图5（b）所示。运算时间为3.39 s。

利用改进FOA优化算法进行仿真时，设定初始位置（1，1，0），目标点（100，100，0），种群规模 20，迭代次数 500。规划路径，结果如图6（a）所示，迭代次数如图6（b）所示。运算时间4.17 s。

由以上两组仿真结果对比分析可知，使用改进FOA算法多次进行路径规划均不会陷入局部最优，表明了算法的稳定性和有效性；但种群数目越多，搜索出的路径越短，速度越快，迭代次数也越少。

图4 FOA路径规划结果Fig.4 Path planning based on FOA

图5 改进FOA路径规划结果Fig.5 Path planning based on modified FOA

图6 改进FOA路径规划结果Fig.6 Path planning based on modified FOA

5 结 论

根据月球车遥操作系统中全局路径规划的要求，对果蝇优化算法进行修改并将其用于全局路径规划。考虑到果蝇优化算法易于陷入局部最优的问题，将果蝇与原点的距离直接带入味道浓度判定函数，通过仿真表明，该算法具有规划速度快、全局寻优能力强、不易陷入局部最优的特点，能够很好地找到全局优化路径。

[1]孙纯哲，桂贵生，韩东，等.基于蚁群算法的移动机器人路径规划研究与应用[J].合肥工业大学学报:自然科学版，2006，29（10）:1208-1211.SUN Chun-zhe，GUI Gui-sheng，HAN Dong，et al.Algorithm for mobile robot path planning based on the ant colony algorithm and its application[J].Journal of Hefei University of Technology，2006，29（10）:1208-1211.

[2]彭松，贾阳.基于粒子群优化算法的月面巡视器全局路径规划[J].航天器工程，2012，21（1）:11-16.PENG Song，JIA Yang.Global path planning for lunar rover based on particle swarm optimization algorithm[J].Spacecraft Engineering，2012，21（1）:11-16.

[3]朱庆保.动态复杂环境下的机器人路径规划蚂蚁预测算法[J].计算机学报，2005，28（11）:1898-1892.ZHU Qing-bao.Ants predictive algorithm for path planning of robot in a complex dynamic environment[J].Chinese Journal of Computers，2005，28（11）:1898-1892.

[4]Wen-Tsao Pan.Fruit fly optimization algorithm[M].Taipei:Tsang Hai Book Publishing Co.，2011.

[5]吴小文，李擎.果蝇算法和5种群智能算法的寻优性能研究[J].火力与指挥控制，2013，38（4）:17-20.WU Xiao-wen，LI Qing.Research of optimizing performance of fruit fly optimization algorithm and five kinds of intelligent algorithm[J].Fire Control&Command Control，2013，38（4）:17-20.

[6]张珗，李清毅，许晓霞.月球表面地形数学建模方法[J].航天器环境工程，2007，24（6）:341-343.ZHANG Yue，LI Qing-yi，XU Xiao-xia.Mathematical modeling oflunarsurfaceterrain[J].SpacecraftEnvironmentEngineering，2007，24（6）:341-343.