数字保存项目的投资决策研究
——基于项目投资成本不确定性的分析
2014-01-13臧国全李思思
●臧国全,李思思
(郑州大学信息管理学院,郑州450001)
数字保存项目的投资决策研究
——基于项目投资成本不确定性的分析
●臧国全,李思思
(郑州大学信息管理学院,郑州450001)
数字保存项目;投资决策;模型
数字保存项目的成本不确定性包括外部成本不确定性和内部成本不确定性。本文构建了外部成本不确定下的投资决策模型、内部成本不确定下的投资决策模型和两种成本均存在不确定下的投资决策模型,并求解了这三种类型的投资决策模型,得出了在不同类型成本不确定条件下的投资决策规则。
数字保存项目的投资决策是指针对该类项目寻找最优投资条件,以期在该条件下进行投资获得的收益最大化。成本和收入是投资决策的影响因素,与一般投资项目相比,数字保存项目的成本构成和收入来源有一定的特殊性。笔者已经对成本确定条件下的数字保存项目投资决策进行了研究,[1-3]因此,本文的研究内容是笔者已有研究的延续。
最优投资条件有两大类:一是收入的临界值,二是成本的临界值。在成本确定,收入不确定时,最优投资条件是数字保存项目的期望收入大于收入临界值;在成本不确定,收入确定时,最优投资条件是期望投资成本小于成本临界值。其中第一类笔者已研究,本文的研究是第二类,就是寻求成本临界值,以及对成本临界值有直接影响的要素(如投资机会价值等)进行分析。
1 数字保存项目成本类型及其对投资决策的影响
1.1 成本的类型
数字保存项目的成本构成主要有两大类:外部成本和内部成本。前者是指成本要素的价格取决于项目之外的经济市场和相关政策,而后者则是指成本要素的价格由项目本身所决定。
1.1.1 外部成本
(1)基础设施建设成本。主要包含两类:数字保存系统和其他基础设施。数字保存系统的基础设施包括硬件和软件,硬件设备如计算机和网络设施、海量数据存储设备、异地备份系统等;软件如数据库软件、系统管理软件、OCR识别软件、网络数据安全软件等。其他基础设施包括生产和办公建筑及其配套设备等。这类成本大多为固定成本。
(2)数字资源的产权许可成本。这类成本与知识产权的法律和政策有关,如产权年限的规定决定了数字资源是否需要进行产权许可。然而,产权许可的费用多少一般由数字保存项目与产权所有人协商,因此,该项成本也具有内部成本的特征。
(3)人力资源成本与原材料成本。前者包括管理人员、生产人员和销售服务人员的薪酬,后者包括数字保存项目在生产和用户服务过程中产生的各种消耗材料。虽然现实中人力资源成本看似为内部成本,但实际上与整个经济和市场息息相关。
1.1.2 内部成本
(1)生产成本。指数字保存项目在生产过程中每个工序产生的费用。这些工序主要有:原始数字资源的生产、获取与质量检验;原始数字资源到SⅠP[4](SubmissionⅠnformation Package,提交信息包,取自于ⅠSO14721《OAⅠS参考模型》标准术语)的转换;SⅠP的质量检验与控制;SⅠP到AⅠP[5](ArchiveⅠnformation Package,保存信息包,取自于ⅠSO14721《OAⅠS参考模型》标准术语,AⅠP的组成包括数字对象、表征信息和保存描述信息三部分)的转换;AⅠP的质量检验与控制;元数据析出成本;AⅠP的保存,AⅠP的数字迁移等。这类成本大多为可变成本。另外,销售成本也可以划为该范畴,如广告宣传。
(2)管理成本。包括常规管理成本和技术管理成本。前者发生的管理项目诸如数字保存方针的制定与评审;灾难性事件应对方案制定、测试及其数据恢复;项目风险识别、评估与管理等。后者发生的管理项目诸如关键过程变更的效果测试与变更复原;软件技术环境监控及其监控信息的评估、软件的更新;硬件技术环境监控及其监控信息的评估、硬件的更新等。
(3)数字保存项目的自开发技术成本。保存技术有两类:移植技术和自开发技术。前者指将其他领域中使用的技术直接应用在数字保存项目中,属于项目的外部成本,数字保存项目基础设施建设中的几乎所有技术和生产过程中的一些技术都属于这个范畴。后者主要涉及数字保存项目生产和管理中的一些技术,这类技术成本的变化取决于项目本身。
1.2 成本不确定性的影响因素
(1)外部成本不确定性的影响因素。外部成本的价格变动与数字保存项目本身无关,只与整个经济、市场乃至相关法律法规和政策相关。因此,外部成本不确定性的影响因素都是外部因素。如ⅠT技术的发展会导致数字保存系统基础设施建设成本和移植技术购买成本的变化;数字资源的不同产权状态对产权许可成本有着直接影响,当然产权状态由知识产权法界定,所以数字保存的相关法律政策是一个重要因素;市场是人力资源成本和原材料成本的决定者,工资的变化和原材料的价格都与整个经济发展相关。无论项目是否投资,外部成本的变化都呈随机性,并且时间跨度越长,不确定性越大。
(2)内部成本不确定性的影响因素。由于内部成本仅与数字保存项目本身有关,所以内部成本不确定的影响因素都是项目内部的因素。如管理水平与管理规范程度影响管理成本;人员技能水平和岗位职责的制定与落实将影响各个工序的生产质量,从而直接影响生产成本。只有实施项目并且直到完成,内部成本的不确定性程度才能最终明晰,因此,在项目进展过程中,实际成本常常偏离预期成本。
本文假定数字保存项目的收入是确定的。
1.3 成本不确定性对投资决策的影响
上述两种类型的成本不确定性都会增加数字保存项目的投资机会价值,原因在于投资机会价值是成本的凸函数。假设C为成本,B为项目收入,投资机会价值函数为max[0,B-C]。这种投资机会类似于金融期权中的看跌期权,也即期权持有者拥有以固定的执行价格B销售一个不确定性C的资产,因此,当这份资产的价格变动增加时,该期权的价值将随着增加。
然而,这两种类型的成本不确定性对于最优投资决策的影响方式不同。内部成本不确定性将导致项目完成所需期望成本临界值的提高,因此,当一个数字保存项目的期望成本使得传统的NPⅤ(净现值,指收入与成本之差)为负值时,如果成本变化的方差足够大,该项目的投资在经济上也可能是可行的,原因在于只有投资才会揭示内部成本的信息。另外,因为有关成本的信息只有进行投资才能获得,所以等待没有价值,延迟期权价值[5]永远为零。
外部成本的不确定性会降低期望成本的临界值,因此,如果一个数字保存项目的NPⅤ为正值,但由此进行投资可能也是不经济的。原因在于,无论是否投资,外部成本都会出现波动情况,因此,对于大多数字保存项目的投资来说,延迟期权价值都大于零。
2 数字保存项目的投资决策模型构建
2.1 成本确定下的投资决策模型构建
为了与成本不确定形成对比,首先考察一下成本确定时的数字保存项目投资决策模型。
在成本确定情况下,由于已经假设项目的收入是确定的,因此这种情况下唯一的不确定变量是无风险利率。假设数字保存项目的实际成本为一个随机变量~,期望成本为C=E(~),项目完成需要一定时间跨度,最大投资率为Ⅰm,项目收益为已知确定值B。项目按照最大投资率进行投资,完成所需的时间跨度为T=C/Ⅰm,因此投资机会价值为:

其中,r为无风险利率。数字保存项目的最优投资规则为F(C)>0,也即C小于投资成本的临界值C*:
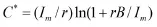
图1展示了B=10,Ⅰm=2,r分别为0、0.1、0.2三种情况下的F(C)的函数曲线。
由图1可知,如果r=0,那么F(C)=B-C,C* =B。但是,如果r>0,那么F(C) 图1 成本确定下的投资价值曲线 2.2 成本不确定下的投资决策模型构建 2.2.1 成本不确定性的描述模型 在数字保存项目建设过程中,剩余投资额随着投资过程的时间延长而减少,但同时呈现随机变化。假设t时刻剩余投资额为C(t),那么其变化过程可用下述方程式描述: 其中,Ⅰ(t)为投资率,g(Ⅰ,C)是一个有关内部成本和外部成本的变化函数,z(t)为维纳过程。[6]C的随机变化要么由内部成本不确定性引起的,要么由外部成本不确定性引起的,要么由两者的共同作用引起的。 令F(C)为投资机会价值,那么F(C)应该满足: 上式中,μ为折现率,T为项目完成所需时间,并且0≤Ⅰ(t)≤Ⅰm,C(T)=0。 为了使式(2)和式(3)有经济意义,需要进行如下限制:①Fc<0,即投资成本的增加会降低投资机会价值;②dC的瞬时方差值以C为边界,并且当C→0时,该方差也趋于0;③如果以最大投资率Ⅰm进行投资,那么,,因此,C为项目完成的期望成本。为了满足上述限制,可以证明g(Ⅰ,C)的形式为,并且 为了简化模型,本文将α的取值限制在0和1/2两种情况,以寻求最优投资的简单两极解。这两种情况分别对应于成本不确定性的两种形式。α=1/2对应于内部成本不确定性,只有在项目投资时C才能发生变化,并且dC/C的瞬时方差与Ⅰ/C呈现线性关系。在项目投资时,C在△t时段内的变化期望值为-Ⅰ△t。 α=0对应于外部成本的不确定。dC/C的瞬时方差是一个常量,并独立于Ⅰ。即使没有投资,C仍然有波动。无论项目的进展如何,外部成本随市场的变化都将引起C的变化。 综合考虑不确定性的两种形式,结合上述针对两种情况的讨论,可以推导出C的简单形式为: dz和dw分别是两个不相关的维纳过程的增量。第二项是有关内部成本不确定性的描述,β为内部成本不确定性的系数,dz为内部成本不确定性的变化,该变化与整个经济无关。第三项是有关外部成本不确定性的描述,γ为外部成本不确定性系数,dw为外部成本不确定性的变化,该变化与整个经济相关。 2.2.2 成本不确定下的投资决策模型 投资决策模型的构建可以采用动态规划法的贝尔曼方程。[7]针对式(3)进行贝尔曼方程转换,再将式(4)代入,得出的数字保存项目投资机会价值F(C)的微分方程如下(参考Robert S.Pindyck的推导,[8]推导过程复杂,略): 由式(5)可知,F(C)是Ⅰ的线性函数。因此,要使投资机会价值F(C)最大化,投资率Ⅰ必须满足: 所以式(5)存在一个临界值C*,当C≤C*时,Ⅰ(t)=Ⅰm;否则,Ⅰ(t)=0。为了求出F(C)和C*,式(5)必须满足下列边界条件: 式(7)的涵义是当项目完成时,收益为C。式(8)的涵义是当C趋于无穷大时,在项目的生命周期内进行投资的机会非常小。式(9)延续了式(6)的涵义,并且F(C)在C*处是光滑连续。 3.1 内部成本不确定下的投资决策模型求解 当仅存在内部成本不确定时,即γ=0,式(5)变为: 在这种情况下,只有进行投资,C才会有变化,因此,当C>C*时,项目不会投资,F(C)=0。所以,边界条件(7)和(9)不变,但边界条件(8)变为F(C*)= 0。下面根据r的不同取值进行分别讨论。 3.1.1 无风险利率r=0时的求解 当r=0时,式(10)有一个解析解(推导过程复杂,略): C的临界值C*为(推导过程复杂,略): 式(11)可简单解释为:投资机会价值的期望值为B-C,后面一项描述投资机会价值的随机变化情况。另外,当β≠0时,C*>B,并且C*随β的绝对值增加而增加。这说明,内部成本不确定性越大,投资成本的临界值也越大,投资机会价值也越大。 3.1.2 无风险利率r>0时的求解 当r>0时,式(10)没有解析解,只有通过设置不同的值采用数值法求解。因为数值法得出的求解是一系列离散数据,所以有必要描绘出解的特征。下面分析在不同参数值的情况下投资机会价值F(C)和投资成本临界值(C*)的基本特征。 为了选择合理的值,需要将与项目总成本变化的方差联系起来。参考Robert S.Pindyck的研究,[8]在γ=0的情况下,项目投资总成本变化的方差为: 根据式(12),当成本变化的标准差与期望成本的比例从25%到50%时,β的值将从0.343到0.63。在实际应用中,数字保存项目成本变化的标准差在区间[25%,50%]是很合理的。 (1)投资机会价值F(C)解的基本特征。图2采用了的上述值描绘出对F(C)的影响。可以看出,在的三种取值中,F(C)作为C的函数,越大,F(C)也越大。另外,只有当=0.63时,C*的值才会超出B(即10)。 图2内部成本不确定下C对F(C)的影响 图3 显示了F(C)对最大投资率Ⅰm的依赖关系。可以看出,最大投资率的增加会导致投资机会价值F(C)的增大,这是因为投资率的增加意味着项目的收益B获得时间提前,因此折现越小。 图3 内部成本不确定下最大投资率Ⅰm对F(C)的影响 (2)投资成本临界值C*解的基本特征。图4显示的是C*作为β的函数曲线。C*随β的增加而增加,当C*的值从9增加到13.5(大约增加50%)时,β的值增加到1左右,此时这意味着整个成本变化的标准差为期望成本的100%。所以,内部成本的不确定越大,投资成本的临界值也越大。 3.2 外部成本不确定下的投资决策模型求解 当仅存在外部成本的不确定性,此时β=0,式(5)将变为: 边界条件(7)和(8)仍然有效,但是条件(9)变为FC(C*)=-1(由于β=0)。这种情况下,无论项目是否投资,C都会变化。 图4 内部成本不确定下β对C*的影响 当γ>0时,如果r=0,式(13)无解,因为没有理由进行投资,项目总是等待到C接近0以获取最大净收益为最好,因为收益不存在折现,所以可以等待足够长时间期盼这种情况发生。 如果Ⅰ=0,γ的合理取值依赖于成本的构成,如0.20这个值对于数字保存项目人力资源成本变化来说较高,但对于项目基础设施建设所需的大多数成本要素(如计算软硬件)的成本变化来说较低。图5展示了式(13)的数值解,可以看出,即使γ=0.20,γ对投资机会价值和投资临界值C*都有足够大的影响。当γ=0.20时,C*的值大约为γ=0时的一半,此时的决策规则应该是项目收益为期望成本的大约2倍。所以,外部成本的不确定性也具有非常大的作用。 图5外部成本不确定下对F(C)的影响 3.3 一般情况下的投资决策模型求解 图6 外部成本不确定下对F(C)和C*的影响 此种情况下,γ≠0并且β≠0,可以证明,方程式(5)没有解析解,只有数值解。在参数β、γ、和φ的不同组合情况下,通过数值方法对式(5)以及相关边界条件进行求解,可以获得成本临界值C*和投资机会价值F(C)。 3.3.1 投资成本临界值C*解的特征 表1和图7展示的是在参数取值为φ=0、B=10、Ⅰm=2和r=0.05的情况下,β和γ参数取不同的值,对式(5)及其边界条件进行数值法求解得出的C*值。可以看出,C*与γ与呈反变关系,与β呈正变关系,但对γ的变化更敏感。无论β取何值,γ=0.5时的C*值大约是γ=0时C*值的1/4。因此,外部成本不确定性的增加对项目投资本身不利,然而由于数字保存项目属于一种高新技术项目,这类项目外部成本占的比例并不高,所以该类项目对外部成本变化的敏感度不是很高。反过来,数字保存项目中内部成本占的比重较大,所以内部成本的不确定性对该类项目的影响更大些。 表1 C*作为β和γ的函数(B=10,Ⅰm=2,r=0.05,φ=0) 图7是将表1以可视化形式展示的结果。 图7 C*作为β和γ的函数 3.3.2 投资机会价值F(C)解的特征 表2和图8展示了F(C,β,γ)作为β和γ的函数值(C=8.92,该值是β=γ=0时的C*的值,见表1)。可以看出,F的值与β和γ均呈正变关系,但对γ更敏感。当γ的值较大时(如γ=0.5),随着β的增加,F的变化很小。 表2 F(C,β,γ)作为β和γ的函数值 图8 是将表2以可视化形式展示的结果。 图8F(C,β,γ)作为β和γ的函数值(C=8.92)3.4模型的应用 为了应用本文设计的模型求出投资机会价值和最佳投资成本临界值,必须估算出数字保存项目成本的β、γ和φ的值。在实际操作中,需要估算出每个成本项不确定性的置信区间。为了把成本划分为内部成本和外部成本,可以采用一个基本特征:前者独立于时间,而后者每个成本项的成本变化与时间呈线性关系。 本文将数字保存项目的成本分为项目外部成本和项目内部成本,构建了成本不确定性的描述模型,并在此基础上建立了成本不确定下的投资决策模型,并对外部成本不确定下的投资决策模型、内部成本不确定下的投资决策模型和这两类成本都不确定下的投资决策模型的求解进行了讨论。 然而,本文的研究也存在局限性:一是假设数字保存项目的收入是确定的,这与现实情况存在一定差距。实际上,数字保存项目的收入呈现出几何布朗运动更贴近实际,那么,怎样建立投资成本与项目收入同时为随机变化的投资决策模型,并寻求该模型的解析解或数值解,是本文的后续研究之一;二是为了简化模型和求解的方便,在成本变化的模型中将参数的值限定在要么取0(对应于外部成本的不确定性),要么取1/2(对应于内部成本的不确定)。实际上,应该取消上述限制,回归的值为0≤α≤1/2,因此,寻求更一般的投资规则,是本文的后续研究之二。 [1]臧国全,等.基于延迟期权的数字保存项目投资规则建立——基于对用户数量的离散变化分析[J].图书馆理论与实践,2013(7):27-30. [2]臧国全,安明.数字保存项目建设中延迟期权作用分析[J].情报科学,2013(7):10-14. [3]臧国全,等.数字保存项目的投资时机研究[J].情报科学,2013(1):9-13. [4]National Aeronautics and Space Administration.Reference Model for an Open ArchivalⅠnformation System(OAⅠS)[EB/OL].[2013-02-10].http://public. ccsds.org/publications/archive/650x0b1.pdf. [5]百度百科.延迟期权[EB/OL].[2013-03-01]. http://baike.baidu.com/view/5128634.htm. [6]百度百科.维纳过程[EB/OL].[2012-03-25]. http://baike.baidu.com/view/652663.htm. [7]百度百科.贝尔曼方程[EB/OL].[2013-05-01].http://baike.baidu.com/view/5209760.htm. [8]Robert SPindyck.Ⅰnvestments of UncertainCost[EB/ OL].[2013-02-19].http://www.nber.org/papers/ w4175. G250 A 1005-8214(2014)08-0036-06 臧国全(1963-),男,教授,博士,博士生导师,发表论文70余篇,研究方向:数字保存;李思思(1990-),女,在读研究生。 2013-09-16[责任编辑]菊秋芳 本文系国家自然科学基金项目“数字保存经济要素与经济评价研究”(项目编号:71173197)研究成果之一。


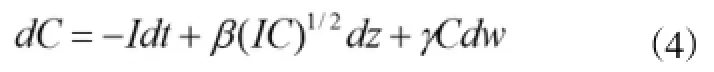
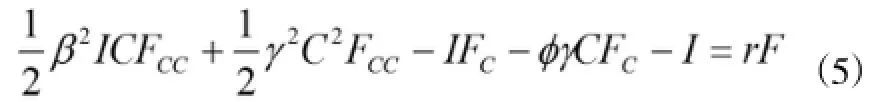


3 成本不确定下的投资决策模型求解


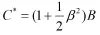











4 结论
