基于相关峰插值的五元十字阵被动声定位算法

马少春，刘庆华，黄灵鹭

（桂林电子科技大学信息与通信学院，广西 桂林541004）

0 引言

在电子对抗领域内，被动声定位技术是指利用目标声信号获得目标位置信息的技术，具有隐蔽性好、不受通视条件限制等优点。目前使用传声器阵列对声源进行定位的方法主要分为三类：时延估计、谱估计和定向波束形成。基于时延估计的方法是指利用声源发出的信号到达各个传声器的时间延迟对声源位置进行估计，自广义互相关算法［1］提出以来，由于其计算速度快，能达到实时的要求，定位精度较高，而得到广泛应用。

被动声定位在实际应用时往往受到各种因素的限制，如时延估计精度、基阵尺寸、目标距离等［2］，特别是对时延估计的精度要求很高，所以准确地进行时延估计是被动声定位的关键。常规的互相关时延估计算法［3］是基于快速傅里叶变换（Fast Fourier Transform，FFT）计算信号在频域的互谱进而计算时间延迟的，计算得到的时延间隔为采样周期的整数倍，时延估计精度为Ts／2，自适应时延估计算法［4］精度虽优于传统互相关算法，然其收敛速度较慢计算量较大不利于实时实现。针对互相关时延估计方法使用FFT 进行快速计算会在频域产生栅栏效应影响时延估计精度的问题，提出基于相关峰插值（Fine Interpolation of Correlation Peak，FICP）方法［5］的五元十字阵［6-7］被动声定位算法。

1 被动声定位原理

对于空间中的确定声源，由于声信号到达各点传声器时刻各不相同，因此可以利用时间延时计算出距离差值，进而建立几何关系求出目标位置信息。确定目标声源在三维坐标系中的三个位置参数需要通过四个传声器获得三个独立的时延值，而五元十字阵克服了四元十字阵定位误差与目标方位角有关的问题且十字阵具有分维特性，阵列冗余度较小，因此系统中阵型结构采用五元十字阵。平面五阵元十字形阵列是由四元十字阵的中心点加一个声传感器构成，如图1所示。

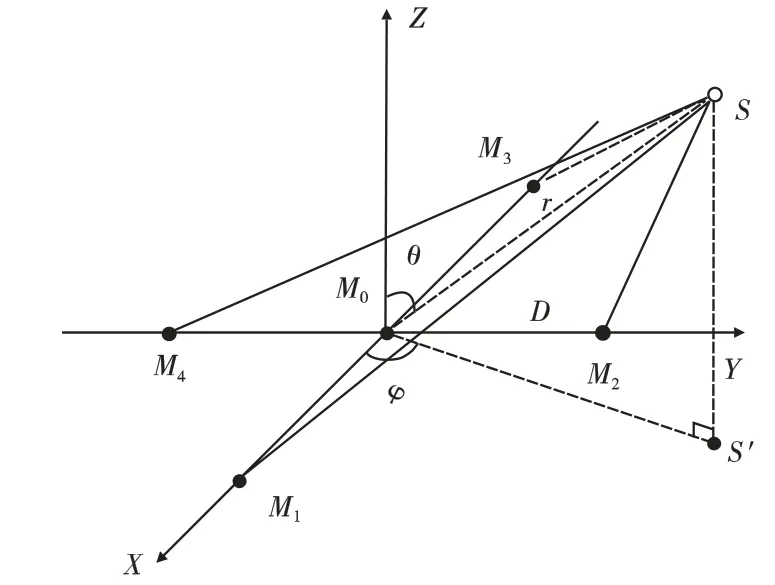
图1 五元阵示意图Fig.1 Five-elementcross array schematic diagram

图中五个阵元的坐标分别为M0（0，0，0），M1（d，0，0），M2（0，d，0），M3（-d，0，0），M4（0，-d，0），目 标声源S的球坐标表示为（r，φ，θ），其中r为目标S到坐标原点的距离，φ 为目标s的方位角，即目标点S 在五元十字阵平面的投影与x 轴正方向的夹角（x 轴正方向约定为从传声器M0到传声器M1的方向），θ为目标点S 的俯仰角（即五元阵平面法线与传声器M0和目标点S 连线的夹角），d 为阵列孔径，C 为空气中声音的传播速率。定义τi=t0-ti（ti为声源到达传声器i 的时刻），则声源到达各个传感器M1，M2，M3，M4与到达传感器M0的时延可分别记为τ1、τ2、τ3、τ4，由 声 阵 和 目 标 的 几 何 位 置 有 如 下 方程组：可得目标的定位方程为：

考虑实际中目标位于远场，此时有

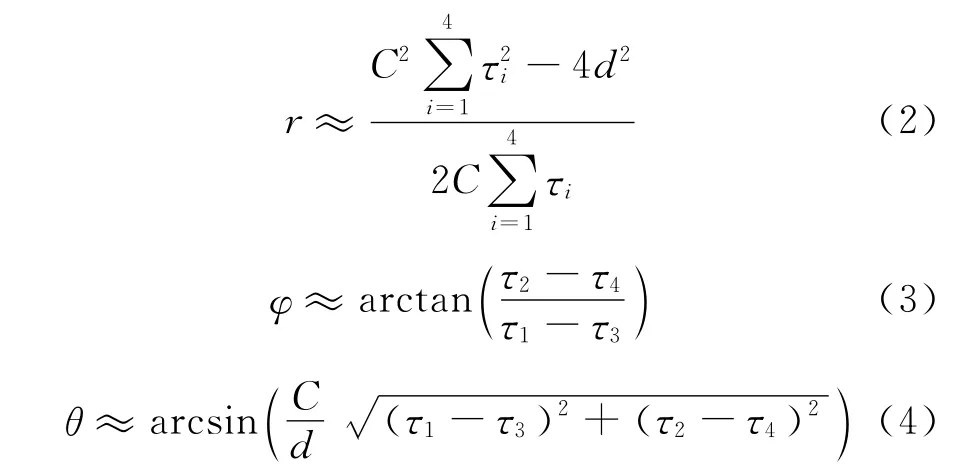
式（2）求出的方位角范围是-π／2，π／

［］2 ，实际中可通过判断φ 值正负、τ1与τ3的关系来确定目标投影所在象限对方位角进行修正。由观测信号计算出到达传声器的时延差值，利用式（2）-式（4）即可求得声源目标在五元十字阵中的球坐标参数。

2 基于相关峰插值的定位算法原理

假设两个传声器接收的信号模型为：

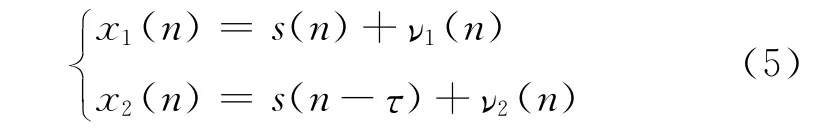
其中，s（n）为声源信号，τ为时延，ν1（n）、ν2（n）表示加性噪声。

给 定 一 个 新 变 换 MCZT（Modified Chirp Z Transform）及逆变换IMCZT 计算信号的细化频谱：

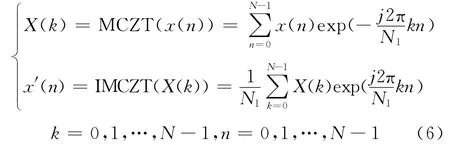
式中，x（n）序列长度为N，频谱X（k）的间隔由N1决定，Δf=fs／N1，fs为采样频率。逆变换IMCZT求得的x′（n）≠x（n），其计算相当于对MCZT求共轭。MCZT 变换形式与FFT 变换相同，可用FFT 算法实现快速计算。利用MCZT 计算两路信号细化的频谱和互谱，在频域对互谱补零可以提高相关函数波形的分辨率。

两路信号MCZT 变换为：

式中k=0，1，…，N-1。

根据相关定理计算得两信号的互谱

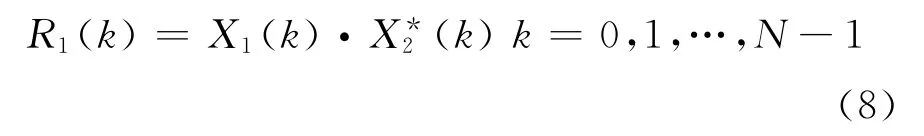
此处R1（k）只是谱的前一部分，通过谱的共轭对称性，可以获得两信号N1点的互谱R2（k）：

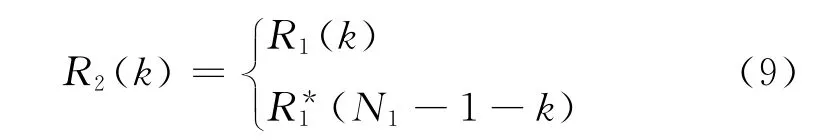
为提高相关函数的分辨率，对互谱R2（k）补零，扩充为N2（N2≥N1）点的序列R（k），最后对R（k）进行逆变换得到两信号的相关函数r（n）：

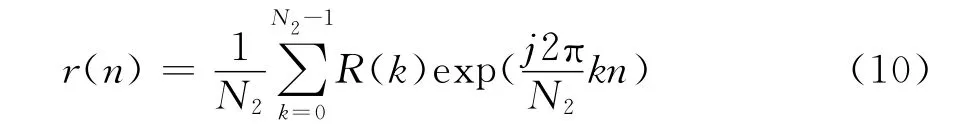
其中n=0，1，…，N2-1。

从式（10）可以看到，相关函数的分辨率由Δt0=1／fs提高到了Δt0=N1＊fs／N2，fs为信号采 样频率。N1、N2应满足N2≥N1≥2 N-1，且N1=2γ（γ为整数），增大N2／N1可以提高相关函数的分辨率。在实际声探测系统中时延差值总是处于有限范围内，相关函数的主峰处在零点附近，因此，对于N2点的r（n）只需取其前N 点与后N 点，组合成相关函数，可以大大降低计算量。

3 算法仿真与外场实验测试

3.1 FICP算法仿真

实验中采用信号x=sin（2πft）exp（-80t），其中f=100Hz，信号长度N 取8192点，采样频率64 kHz，两路信号时延差为0.001 6s，混入高斯白噪声，信噪比SNR=8dB，FICP计算中N1=64 000，N2／N1=10。

图2是两路信号的时域波形，图3采用蒙特卡罗方法分别对基于FICP计算和基于FFT计算的时延结果进行比较。从图中可以看出，当真实时延值处于采样周期整数倍之间时，基于FFT 计算的互相关方法估计的时延值总是为采样周期的整数倍，FICP方法提高了相关函数的分辨率，计算得到的时延值精度更高。

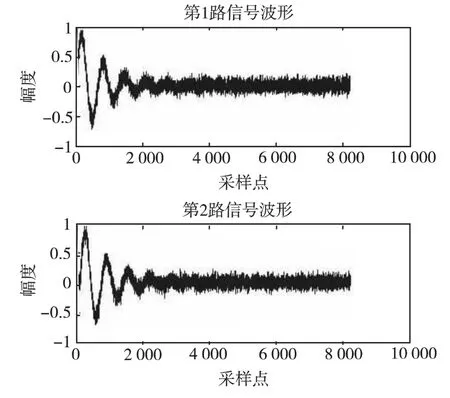
图2 两路信号波形Fig.2 Two-channel signal waveforms

图3 100次计算结果比较Fig.3 Comparison of 100times calculation results

3.2 基于FICP方法的五元十字阵定位算法仿真

实验中采用信号x=sin（2πft）exp（-50t），其中f=100Hz，信号长度N 取8192点，采样频率64 kHz，目标球坐标系坐标为（50，180°，85°），混入高斯白噪声，信噪比SNR=8dB，FICP计算中N1=64 000，N2／N1=10。

传声器得到的五路信号时域波形如图4所示，图5、图6分别为基于FICP 计算和基于FFT 计算的信号相关波形图。仿真中，FICP 计算结果为（48.917，179.908，84.934），误差率为（-2.17%，-0.05%，-0.08%），FFT 计算结果为（47.171，179.848，85.135），误差率为（-5.66%，-0.08%，0.16%），从计算结果不难看出，FICP方法计算的定位精度优于基于FFT 计算的互相关方法的精度。

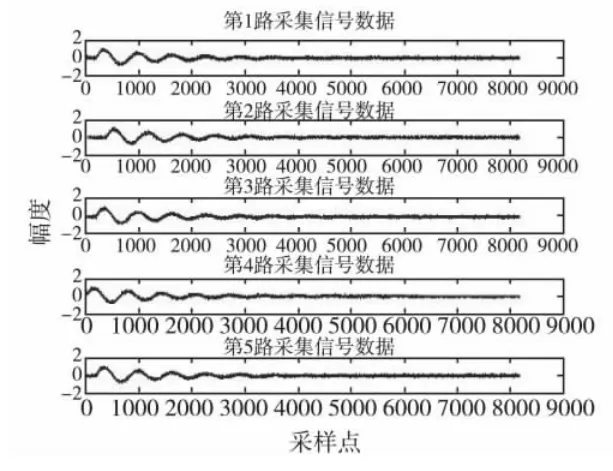
图4 五路信号波形图Fig.4 Five-channel signal waveforms

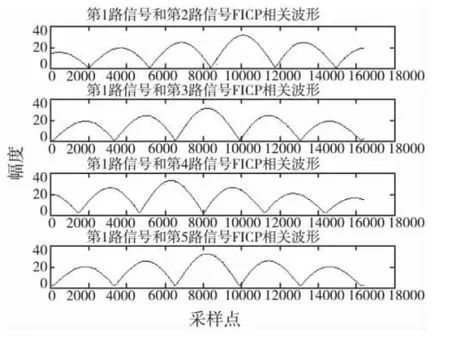
图5 五路信号FICP计算相关波形图Fig.5 Five-channel signal cross-correlation waveforms based on FICP algorithm

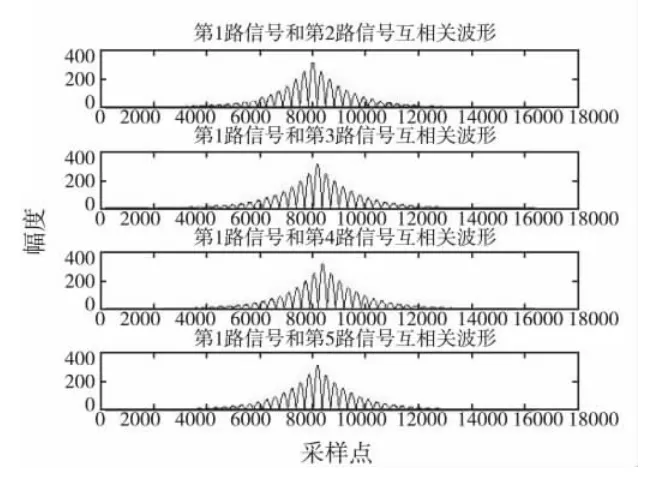
图6 五路信号FFT 计算相关波形图Fig.6 Five-channel signal cross-correlation waveforms based on FFT algorithm

3.3 外场测试实验

如图7所示，声源定位系统主要由传声器阵列、信号调理器、AD采集模块、信号处理模块等组成。其中信号处理模块包含DSP核心板、外部存储器和输出显示部分。传声器阵列将采集的声信号经AD转换送给DSP处理，定位结果由单片机控制液晶屏完成显示。

图7 被动声定位系统框图Fig.7 Passive acoustic location system block diagram

为了验证五元十字阵定位效果，在空旷楼顶进行静止目标的定位实验。实验条件如下：楼顶长宽为50×10m2，播放音效的音响摆放在楼顶天台上，天台高5m，阵列高度可调（0.8～1.2m），实验测试距离取10～45 m，五个传声器布置支架的十字臂上，阵元间距d=1m，传声器型号为CHZ-213，主要性能指标为：全指向性，频率响应20～20kHz，灵敏度56.36mV／Pa，信号调理器×10档输出，信号采样频率Fs=64kHz，采样长度N=16 384点。实验系统如图8、图9所示。

图8 信号调理器和信号处理模块Fig.8 Signal disposal and signal processing module

图9 五元十字阵阵列Fig.9 Five-element cross array

将五个传声器固定好在支架上，连接好系统设备，确定音响与传声器的位置坐标，播放音频信号，记录观测数据。实际测量中，音源固定在距声阵列一定方位作为点声源，通过改变支架位置和转动支架方向来改变目标声源相对位置，完成对被测目标的距离、方位角、俯仰角的实时测量。

在外场试验中，实际测量得到的方位角和俯仰角误差较小，但距离的误差相对较大。此外，由于外场环境存在着干扰，测量的结果会出现抖动，方位角和俯仰角测量结果波动较小，距离测量结果跳动较大，可通过卡尔曼滤波等后置处理方法得到较为准确的测量值。表1、表2和表3对比分析了基于互相关方法的被动声定位算法的结果和基于FICP被动声定位算法计算的目标定位结果，不难看出，基于FICP方法的被动声定位算法性能优于基于互相关方法的定位算法。

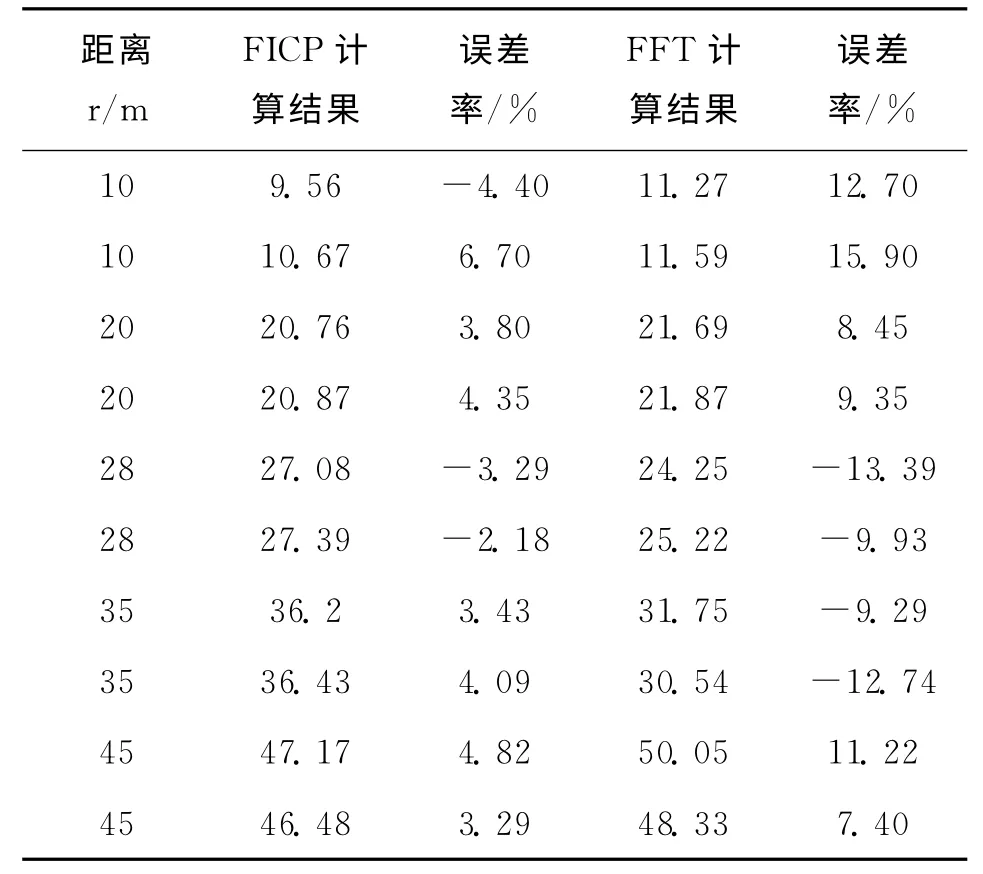
表1 距离测定值Tab.1 The results of distance measurement

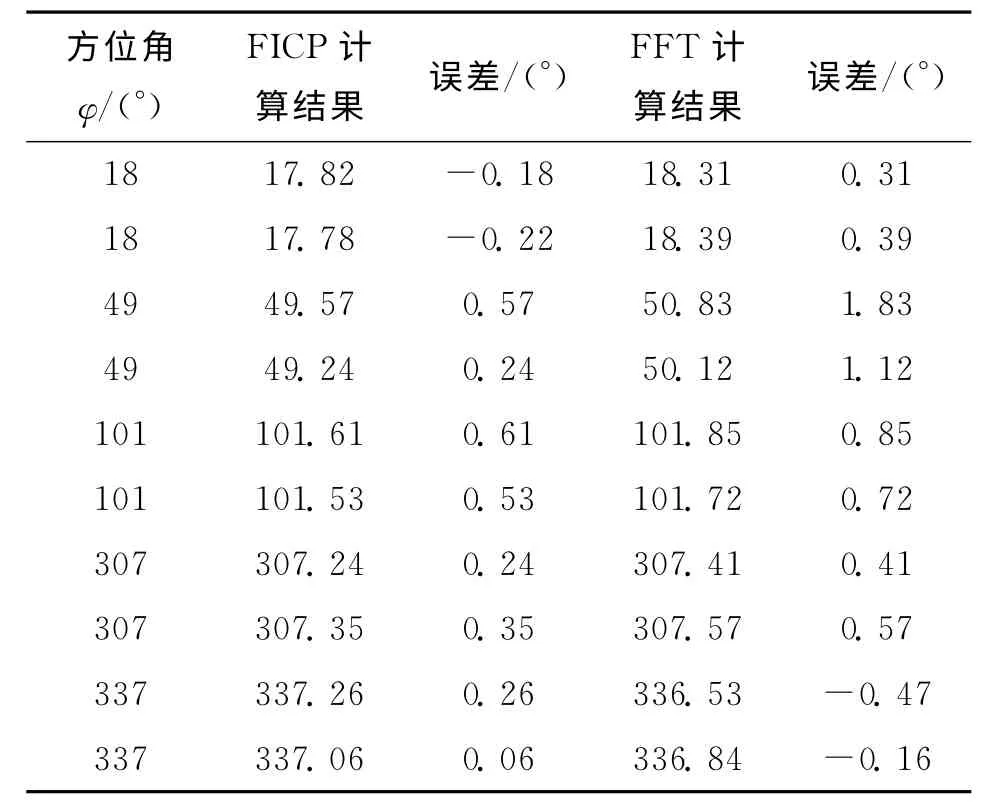
表2 方位角测定值Tab.2 The results of azimuth measurement

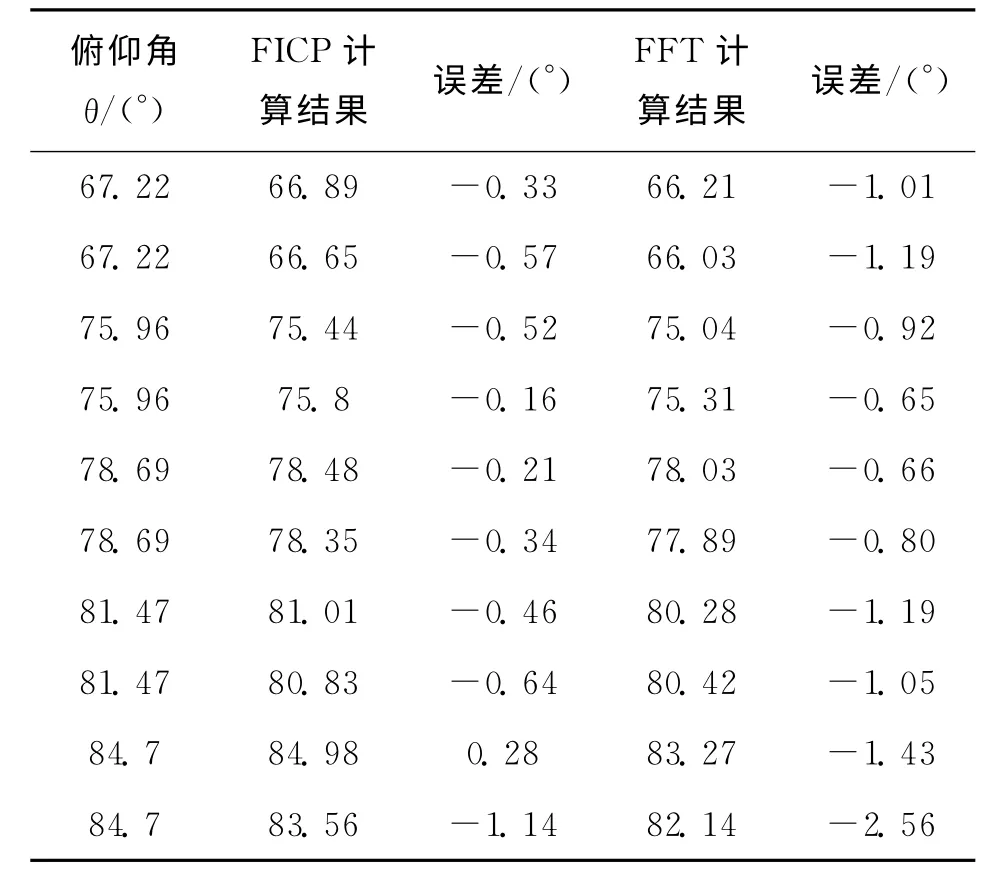
表3 俯仰角测定值Tab.3 The results of pitching angle measurement

4 结论

本文提出了基于FICP 方法的被动声定位算法，对算法的原理进行了推导说明。FICP通过计算信号的细化频谱改善了FFT 变换带来的栅栏效应，并且计算量小可以在嵌入式系统中实时实现。仿真和实验结果都表明，相对于基于互相关方法的被动声定位算法，采用FICP 方法的被动声定位算法能够得到更高的时延估计精度，从而对目标进行更为准确的定位。外场实验中也可以看到，采用FICP方法的被动声定位算法对方位角和俯仰角的定位精度较高，对距离的测量精度以及抗干扰能力有待进一步改善。

［1］Knapp C H，Carter G C.The generalized correlation method for estimation of time delay［J］.IEEE Transactions on Acoustics，Speech，Signal Processing，1976，24（4）：320-327.

［2］陈华伟，赵俊渭.五元十字阵被动声定位算法及其性能研究［J］.探测与控制学报，2003，25（4）：11-16.

［3］罗柏文，于宏毅.采用合成方法的多路信号自适应时延联合估计［J］.信号处理，2013，29（2）：159-164.

［4］黄晓燕，罗建.自适应时延估计算法在被动声定位系统中应用［J］.探测与控制学报，2007，29（2）：73-76.

［5］杨亦春，马驰州.相关峰细化的精确时延估计快速算法研究［J］.声学学报，2003，28（2）：159-166.

［6］向瑾.基于四元十字阵的被动声定位技术研究［D］.太原：中北大学，2008.

［7］黄海军.基于传声器阵列的声源定位系统的初步研究［D］.南京：南京邮电大学，2013.