基于导向矢量实时校准的稳健波束形成算法

乔成林，全厚德，崔佩璋，郑保明

（1.军械工程学院信息工程系，河北 石家庄050003；2.总装备部通用装备保障部，北京110000）

0 引言

自适应波束形成广泛应用于雷达、通信和导航等系统中，它通过调节各阵元权重使得合成方向图在期望方向形成主瓣，干扰方向形成零陷，从而提高接收信号SINR。1969年，Capon提出了使阵列增益最大的最小方差无失真响应（MVDR）波束形成器，即Capon波束形成器。标准Capon（SCB）波束形成器需要精确知道期望信号导向矢量，而实际中由于受到波束指向误差、阵元位置误差和通道误差等，期望信号导向矢量往往失配。此时，Capon波束形成器性能将急剧下降，甚至会将期望信号当作干扰抑制掉［1］。为了提高Capon 波束形成器在导向矢量失配时的输出性能，涌现出许多稳健波束形成算法。常见的稳健波束形成算法可以总结为三类：线性约束法［2］、特征空间法［3］和对角加载法［4］。线性约束法以减少自由度提高稳健性；特征空间法在失配误差增大时，算法性能严重下降；对角加载法的加载值难以确定且会减弱干扰抑制能力。

近年来，一些基于导向矢量不确定集约束的稳健波束形成算法被提出，如文献［5-6］提出基于最差性能最佳化的算法（WCPO），采用二阶锥规划进行求解，但运算量较大。Li等人提出新的稳健波束形成算法（RCB），并证明该算法的解与WCPO 算法相同且运算量较小［7-8］。然而该算法并没有给出求解Lagrange乘子的表达式，而是采用牛顿迭代法求解，实时性较差。戴凌燕等人通过近似推导给出近似解，但近似假设造成计算精度和输出SINR 下降［9］。需要注意的是，上述基于导向矢量不确定集约束的稳健波束形成算法必须精确知道误差范围，而这在实际中是很难做到的。为此，文献［10］提出在一个区域内构造正定矩阵，并用该矩阵特征向量线性表示该区域内所有方向导向矢量。邹翔等［11］人基于该原理提出无需假定误差模约束的失配误差正交分解稳健波束形成算法，取得了不错的效果，且具有较好的实时性。但该算法在构造函数时限定多个约束条件，减少了系统自由度。文献［12］又提出以输出最大功率为目标，构造代价函数，在不减少自由度的情况下，输出SINR 较高，然而其收敛速度较慢，不利于工程实现。本文针对已有稳健波束形成算法实时性差、收敛速度慢、输出SINR 低的缺陷，提出基于导向矢量实时校准的稳健波束形成算法（RCRB）。

1 阵列信号模型和MVDR 算法

考虑一个M 阵元线阵，假设空间远场存在一个期望信号和J个干扰，信号干扰两两互不相关。并假设空间噪声是相互独立的高斯白噪声，且与信号干扰互不相关。则t时刻阵列接收信号为：

其中，a（θ0）和a（θj）（j=1，2，…，J）分别为期望信号和干扰导向矢量，s0（t）和sj（t）（j=1，2，…，J）分别为期望信号和干扰复包络。N（t）为噪声矢量，N（t）= ［n1（t），n2（t），…，nM（t）］。

则阵列协方差矩阵为：

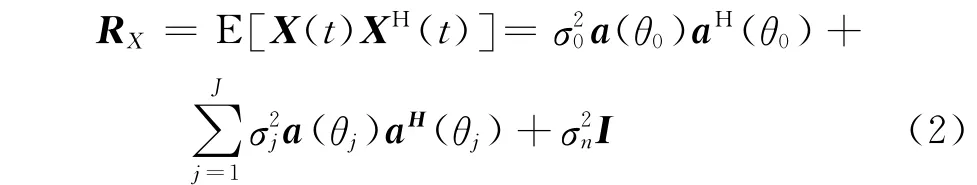
MVDR 波束形成器又称为Capon波束形成器，其思想是让期望信号方向增益约束为1，并使得阵列输出功率最小。该波束设计问题可描述为：

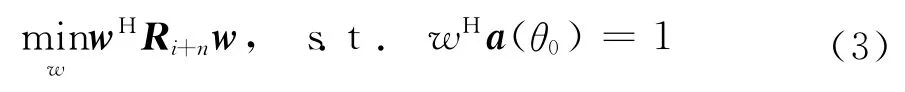
采用Lagrange乘子求解得：

其中，Ri+n为干扰和噪声协方差矩阵。而实际中接收数据往往包含期望信号，无法获得干扰和噪声协方差矩阵。因此，一般直接用接收数据的协方差矩阵RX代替干扰和噪声协方差矩阵Ri+n。另外，期望信号方向往往不能精确可知，一般用估计值代替，即a^（θ0）=a（θ0）。所以，由式（1）-式（4）得MVDR波束形成器权矢量为：

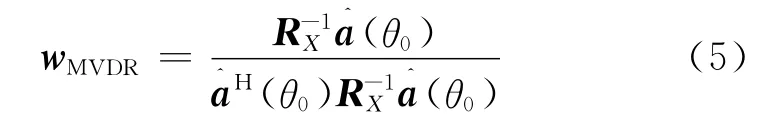
MVDR 波束形成器只有在期望信号导向矢量精确可知时才能获得高分辨力和阵列增益，而实际应用中期望信号导向矢量往往不能精确可知，此时MVDR 波束形成器性能严重下降［1］。本文从真实导向矢量与噪声子空间正交出发，提出基于导向矢量实时校准的波束形成算法可以有效提高系统的稳健性。

2 基于导向矢量实时校准算法

2.1 算法描述

假设期望信号方向θ0包含在内，其中θL和θU分别表示Φ区域的下限和上限，则构造一个正定矩阵ψ［10-12］。

为了便于实现，在计算ψ 时将Φ = θL，θ［ ］U 均匀离散化，则

对ψ 特征值分解，选出P 个较大的特征值，则

其中λ1≥λ2≥… ≥λP≥… ≥λM是相应的M 个特征值，ei（i=1，2，…，M）为其对应的特征矢量，

EP和EQ的列向量分别张成较大特征值对应的子空间和较小特征值对应的子空间。所以，可以对ψ 做如下近似：

根据定义可知，Φ 内所有方向的导向矢量均包含于EP的列向量张成的子空间，则期望信号导向矢量a（θ0）必然包含于这个子空间，也就是说a（θ0）可以用EP的列向量线性表示。

定义一个列向量T（P×1），使它满足式（10）：

所以，求解导向矢量a（θ0）就转化为求解列向量T。

对接收数据协方差矩阵RX进行特征值分解可得：

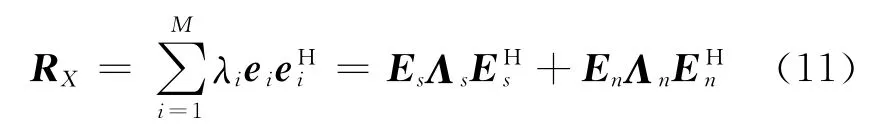
根据子空间理论，真实期望信号导向矢量a（θ0）在信号干扰子空间内，而信号干扰子空间与噪声子空间正交，则真实期望信号导向矢量a（θ0）与噪声子空间正交。则：

式（12）也可表示为：

构造如下代价函数

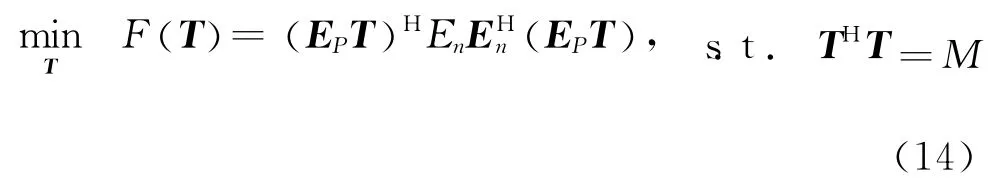
令SU=EHPEnEHnEP，则式（14）简化为：

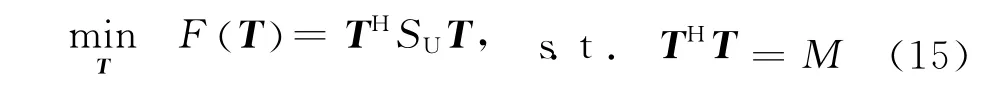
采用最陡下降法迭代求解向量T［10，12］，假设T［n］是T 的当前值，T［n-1］是T 的上一时刻值，T［1］任意设定，则：

An LED light source was used to study settlement of a white ceramic substrate. Specifically, a light with a highly concentrated wavelength and brightness was selected to mitigate the influences that the wavelength and luminance of the chip exercised on the color coordinates of the white LED.

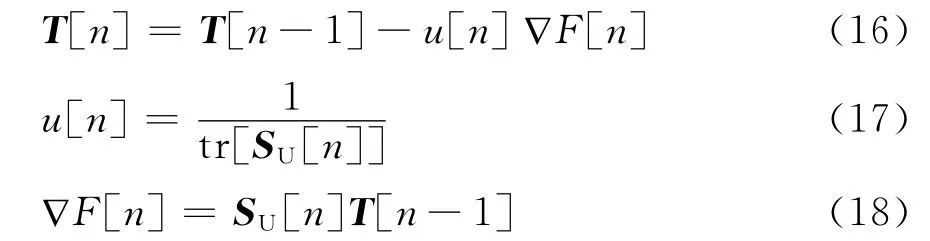
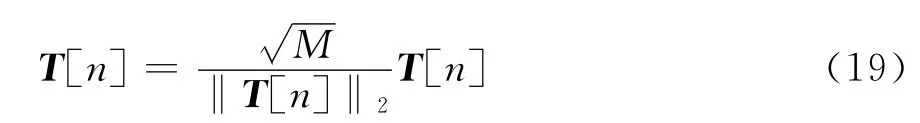
其中u［n］是迭代步长，tr［·］是矩阵的迹。

将T［n］代入式（10）（5），得

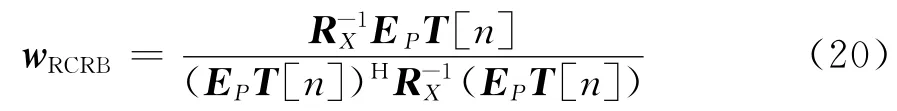
由于噪声的扰动，式（20）获得的权矢量收敛速度较慢。因此，对式（20）采用一种简单而有效的处理，即将权矢量向信号干扰子空间投影，则

2.2算法流程

由上所述，基于导向矢量实时校准的稳健波束形成算法流程总结如下：

步骤1：由式（6）构造一个正定矩阵，并根据式（6）-式（9）得到包含P 个较大特征值对应的特征向量组EP，并定义一个列向量T（P×1），记a（θ0）=EPT；

步骤2：对接收数据协方差矩阵RX特征值分解，得到噪声子空间EnEHn；

步骤3：根据式（6）-式（18）更新列向量T；

步骤5：使用更新后的列向量T，校准导向矢量，并由式（21）得到实时权矢量。

3 仿真实例

为了便于仿真，假设阵列为半波长间距的均匀线阵。假设空间远场包含一个期望信号和两个干扰信号，期望信号和干扰信号两两互不相关，期望信号真实方向为θ0=0°，两个干扰方向分别为θ1=-20°、θ2=50°，干噪比均为30dB。本文RCRB算法假定期望信号方向在Φ=［-5°，5°］内，矩阵Ψ 的较大特征值个数P为6个。每次实验均是100次独立蒙特卡洛实验的平均。将本文提出的算法（RCRB）和标准Capon算法（SCB）、对角加载算法（LSIM）［4］、特征空间算法（ESB）［3］和基于不确定集（RCB）［9］的稳健波束形成算法进行比较。

仿真实例1 导向矢量失配时，阵列波束形成方向图。假设阵元数M =10，期望信号方向观测误差为3°，信噪比为0dB，快拍数为300。LSIM 算法对角加载量为10，RCB算法ε值正好等于导向矢量误差模平方。表1为算法性能对比，图1为阵列波束形成方向图。结合表1和图1可知，当存在导向矢量失配时，SCB算法显然已经失效，甚至将真实期望信号当做干扰进行抑制；LSIM 算法具有一定的稳健性，但仍对期望信号进行部分抑制，所以输出SINR 不高；RCB算法在期望信号方向只下降了0.82dB，且对干扰进行了有效抑制，故输出SINR 较高；RCRB算法和ESB 算法输出SINR 分别为9.68dB 和9.60 dB，均接近理论最优值，但两者实现的方法不同。结合文献［3］可知，当阵元数增加或者存在大角度失配时，ESB算法性能严重下降，下文将详细对比。因此，本文提出的RCRB算法具有更好的稳健性。

表1 算法性能对比Tab.1 Comparison of algorithms

仿真实例2 输出SINR 与导向矢量失配角关系。假设阵元数M=30［3］，信噪比为0dB，快拍数为300。LSIM 算法对角加载量为10，RCB 算法ε值正好等于导向矢量误差模平方。图2 为输出SINR 与信号失配角关系。由图可知，导向矢量失配时，SCB算法性能严重下降，LSIM 算法具有一定的稳健性，但不明显。当小角度失配时，ESB 算法、RCB算法和RCRB算法均具有较好的稳健性，其中RCB算法和RCRB算法输出SINR 要比ESB 算法略高一些。当失配角增大时，结合文献［3］可知，ESB算法存在周期恶化，且阵元数越多，周期越短。而RCB算法在失配角增大时，性能下降的更严重。相反，本文提出的RCRB算法输出SINR 依然很高，不存在周期恶化。因此，RCRB算法具有更好的稳健性，可以在较大失配误差范围内保持良好的性能。仿真实例3 导向矢量失配时，输出SINR 与快拍数关系。假设阵元数M=10，期望信号方向观测误差为3°，信噪比为0dB。LSIM 算法对角加载量为10，RCB 算法ε值正好等于导向矢量误差模平方。图3为输出SINR 与快拍数关系。从图中可知，期望信号导向矢量失配时，SCB 算法、LSIM 算法、ESB算法、RCB 算法、RCRB 算法和理论最优输出SINR 分别为-4.68、7.81dB、9.62dB、8.87dB、9.71dB和9.87dB。所以，RCRB 算法输出SINR要高于其他算法、更加逼近理论最优值。因此，相同条件下，本文提出的RCRB 算法具有更高的输出SINR 和较快的收敛速度。

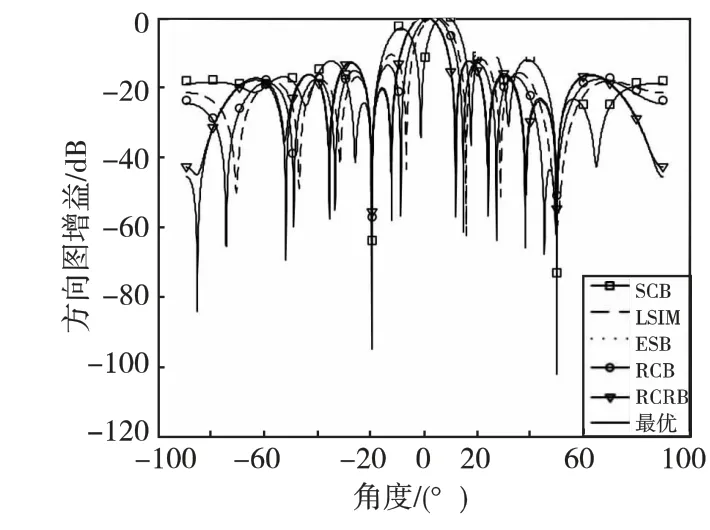
图1 阵列波束形成方向图Fig.1 Beamformer pattern of array

图2 输出SINR 与失配角关系Fig.2 Output SINR versus angle mismatch

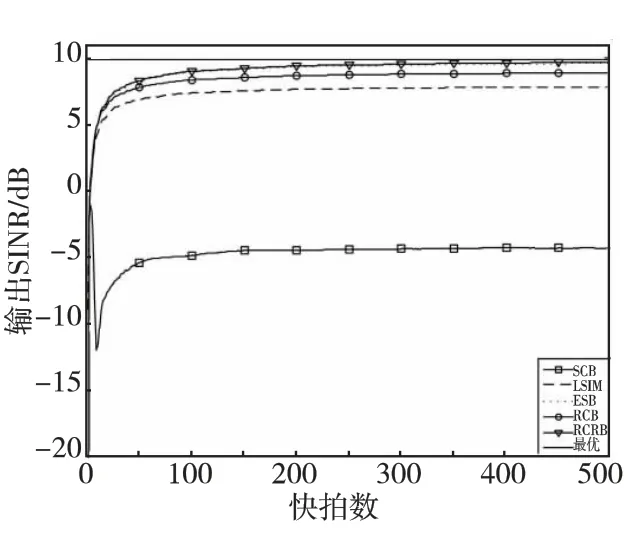
图3 输出SINR 与快拍数关系Fig.3 Output SINR versus the number of snapshots

仿真实例4 导向矢量失配时，输出SINR 与输入SNR 关系。假设阵元数M=10，期望信号方向观测误差为3°，快拍数为300。LSIM 算法对角加载量为10，RCB算法ε值正好等于导向矢量误差模平方。图4为输出SINR 与输入SNR 关系。从图中可知，由于期望信号导向矢量失配，SCB 算法将期望信号当成干扰，造成信号相消现象，随着输入SNR 增大，输出SINR 损失越严重。LSIM 算法在小信噪比时，对导向矢量失配具有一定的鲁棒性，但随着输入SNR 增大，输出SINR 损失严重。RCB算法在输入SNR 小于10dB 时，其输出SINR 较高，当输入SNR 增大时，输出SINR 损失严重，这主要与ε选取有关。RCRB 算法和ESB 算法对输入SNR 变化不敏感，但两者的原理不同，结合图2 可知，随着阵元数增加或信号失配角增大，ESB 算法性能将严重下降。因此，相同输入SNR 下，本文所提的RCRB算法优于其他算法。

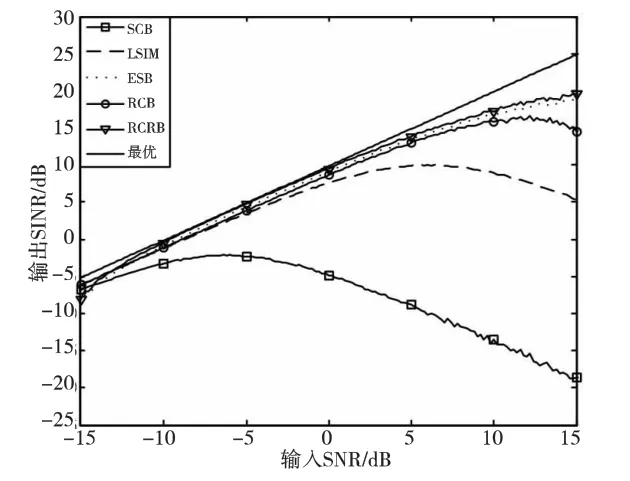
图4 输出SINR 与输入SNR 关系Fig.4 Output SINR versus Input SNR

仿真实例5 导向矢量失配时，RCRB 算法代价函数与快拍数关系。阵元数M=10，期望信号方向观测误差为3°，快拍数为300。图5为RCRB 算法代价函数与快拍数关系。图中最优曲线指真实期望信号导向矢量在噪声子空间上的投影，由于初始阶段信号协方差矩阵存在误差，所以代价函数值较大。随着快拍数增加，代价函数趋于稳定，收敛时最优曲线和RCRB 曲线代价函数值分别为：0.018 和0.063。所以，导向矢量经过RCRB 算法实时迭代后，与真实期望信号导向矢量相差无几，且收敛速度较快，验证了算法有效性。

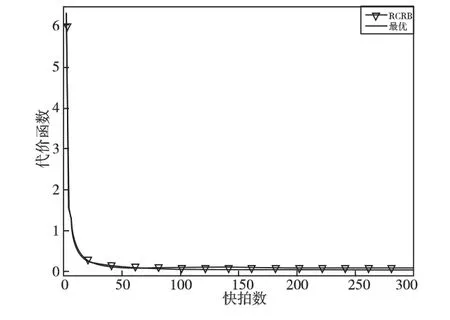
图5 RCRB算法代价函数与快拍数关系Fig.5 The cost function of RCRB versus the number of snapshots

4 结论

本文提出了基于导向矢量实时校准的稳健波束形成算法，该算法首先构造一个正定矩阵，然后根据真实期望信号正交于噪声子空间的原理，建立代价函数，采用最陡下降法自适应迭代求解权矢量，最后将权矢量投影到信号干扰子空间。仿真验证表明该算法实时性好、收敛速度快、输出SINR 高，在较大导向矢量误差范围内仍能保持良好性能，具有较高的实际应用价值，下一步将继续研究其在相干干扰中的应用。

［1］Li J，Stoica P.Robust Adaptive Beamforming.Hoboken［M］.New Jersey：John Wiley ＆Sons，2006.

［2］O L Frost III.An algorithm for linearly constrained adaptive array processing［J］.Proc.IEEE，1972，60（8）：926-935.

［3］程乃平，倪淑燕.改进的特征空间波束形成算法［J］.通信学报，2010，31（8A）：32-36.

［4］Zhang Youwen，Sun Dajun，Zhang Dianlun.Robust adaptive acoustic vector sensor beamforming using automated diagonal loading［J］.Applied Acoustics，2009，70：1029-1033.

［5］Vorobyov S A，Gershman A B，Luo Z Q.Robust adaptive beamforming using worst-case performanceoptimization：A solution to the signal mismatch problem［J］.IEEE Trans Signal Processing，2003，51（2）：313-324.

［6］刘聪锋，廖桂生.基于最差性能最优的稳健STAP算法［J］.电子学报，2008（3）：581-585.

［7］Stoica P，Wang Z S，Li J.Robust Capon beamforming［J］.IEEE Signal Processing Lett，2003，10（6）：172-175.

［8］Li J，Stoica P，Wang Z S.On robust Capon beamforming and diagonal loading［J］.IEEE Trans Signal Processing，2003，51（7）：1702-1715.

［9］戴凌燕，王永良，李荣锋，等.基于不确定集的稳健Capon 波束形成算法性能分析［J］.电子与信息学报，2009，31（12）：2931-2936.

［10］Lie J P，W Ser，C M S See.Adaptive uncertainty based iterative robust Capon beamformer using steering vector mismatch estimation［J］.IEEE Transactions on Signal Processing，2011，59（9）：4483-4488.

［11］邹翔，张旻，钟子发.基于失配误差正交分解的稳健自适应波束形成［J］.电子信息学报，2010，32（10）：2320-2323.

［12］Zhang Wei，Wang Ju，Wu Siliang.Robust Capon beamforming against large DOA mistatch［J］.Signal Processing，2013，93：804-810.