基于多历元相关距离的接收机自主完好性监测

胡彦逢，陆建军，曹可劲，李 豹

（1.海军工程大学导航工程系，湖北 武汉 430033；2.海军装备部综合计划部，北京 100841）

0 引言

传统单历元接收机自主完好性监测（RAIM）算法针对的是出现伪距偏差较大的情况，而当伪距偏差较小，如偏差在米级，由于噪声误差的存在，残余量将淹没在噪声中导致RAIM 失效。针对高精度定位领域对卫星要求较高，卫星即使出现较小偏差也会影响定位精度，必须予以剔除。

文献［1］和文献［2］研究了存在两颗故障卫星的RAIM 算法，但只针对故障量比较大的情况，文献［3］提出基于向量相关距离新型RAIM 算法，该方法可以检测存在多个异常值的情况。目前的文献讨论的一般是故障卫星伪距出现较大偏差的情况，在伪距偏差较小甚至淹没在随机噪声中时，单纯依靠传统的单历元的检测方法很难正确检测出故障星。本文针对传统单历元奇偶矢量RAIM 监测方法存在的缺陷，提出一种新的基于多历元相关距离的RAIM 监测方法。

1 单历元算法与相关距离

1.1 单历元算法

单历元算法，就是只采用一个时刻的数据进行定位解算和RAIM 监测（原理图如图1）。

图1 单历元算法原理图Fig.1 Principle diagram of the single epoch algorithm

RAIM 算法的观测量可通过最小二乘定位解算算法获得，当RAIM 检测到存在故障星，并识别出故障星，然后进行一致性检查，接着将故障信息传送到定位解算阶段，在观测方程中剔除故障星，重新建立观测模型，加速迭代过程，提高定位精度。单颗卫星存在故障的故障检测至少需要5颗可用星，故障识别至少需要6颗星；存在故障时故障检测至少需要6颗星，故障识别需要7颗星。

对系数矩阵G［5］进行奇偶矢量分解，得到正交矩阵q和上三角矩阵R：

其中Q为（n-4）×n维酉矩阵，即行与行之间，列与列之间正交；

p：奇偶矢量，（n-4）×1维矢量；

下面进行特征偏差线一致性检验以检测出故障星。当卫星j发生故障时，奇偶矢量p 和q 的列向量q：，j共线，q：，j分别称为卫星j 的特征偏差线，而特征偏差线和奇偶矢量共线的卫星即为故障星。

故障卫星伪距偏差较小时，单次定位伪距偏差与噪声引起的伪距残余在同一量级时，用传统的单历元检测方法很难成功检测出故障星。由此在第2章提出一种新的RAIM 算法，可以有效克服该缺陷。

1.2 相关距离

衡量向量x和y 之间相似程度常用的相似系数有夹角余弦和相关系数。表征两向量之间的相似程度还可以用相关距离：

当向量x和y 相近时，二者相关距离较小，随着二者的相似性减小，相关距离逐渐拉大。

一般情况下，在进行接收机自主完好性监测中，用到的是相关余弦和相关系数两种衡量指标，这里采用相关距离算法，相关距离算法可以有效检测存在多个异常值的情况，本文在其基础上进行了一定的改进，具体在第2章进行介绍。

2 多历元相关距离改进算法

由于在静态或者低动态条件下用户位置某一分量的定位误差服从零均值正态分布，出现故障时故障星的伪距偏差使得定位误差均值发生偏移，偏移量的大小与伪距偏移量以及卫星的几何分布有关。

当噪声引起的伪距残余是随机的，通过对多次定位结果得到的卫星伪距残余叠加，故障星的伪距残余得到累计，而噪声引起的伪距残余会相抵消，这样便使得故障星的检测概率大大提高。

当某颗卫星伪距的伪距出现较大偏差时，传统的RAIM 方法可以有效检测出，但当伪距偏差在米级甚至厘米以内时，伪距异常值会淹没在噪声里。微小慢变伪距偏差变化较慢，在短时间内（小于2 min）可以认为近似不变，而且在这个过程中假设可见卫星的星座不发生变化。由于噪声的非相关性，它所引起的伪距偏差量同样存在非相关性。通过奇偶矩阵多历元叠加，粗差得到累积而因噪声引起的误差则会相消。由此这里提出一种基于相关距离的多历元算法（原理图如图2）。

(2)固定衰减器2的衰减量的选择应保证发射机的调谐信号到达信号源后的功率低于信号源的最大允许反向输入功率3dB；

同样地，先对观测矩阵进行奇偶矢量分解，然后与伪距残余结合得到奇偶矢量矩阵，将N 个历元的奇偶矢量叠加后获得N 历元叠加矩阵，对奇偶矢量N 历元叠加矩阵求均值：

其中Qi，j是Q 矩阵的元素，pk是奇偶矢量矩阵p 的第k 列的行向量，εk是伪距残余向量的第k 项元素，表示第k颗卫星的伪距残余。

关于衡量指标方面，这里采用相关距离来衡量矩阵RN的第k列（k＜n+1）与第（n+1）列之间的相关性，归一化后可表示为：

衡量指标确定后，进入故障检测部分。假设ε含有一个粗差εi时，RN的第k（k＜n+1）列与最后一列（（n+1）列）之间的夹角余弦会明显变大并接近于1，而相关距离会明显变小，无故障的列相关距离接近于1，存在粗差的那一列与最后一列的相关距离会明显小于其他无故障列。而当ε中含有多个粗差时，由于多个粗差的共同作用，可能将另一颗正常的卫星拉偏，使得该卫星粗差显示异常而发生误判，这就需要系统完善判定标准，以保证RAIM 的可靠性。

图2 多历元算法原理图Fig.2 Principle diagram of several epoch algorithm

3 仿真验证

实验数据采集地点在顶楼，将“卓越航导”BDS／GPS组合导航差分接收机放在空旷处，采集1h静态数据。后续数据处理获得接收机统计平均位置信息，从中提取某时刻9 颗可见卫星的位置信息。设定星钟与接收机时钟相差为固定值1×10-6s，利用卫星位置信息和接收机位置信息产生9颗卫星的模拟精确伪距。在每颗卫星模拟精确伪距上加入方差为0.20 m 的零均值非相关高斯噪声，获得模拟伪距。建立定位解算模型，利用最小二乘法进行定位。

3.1 故障星对定位结果的影响

利用9颗星进行定位解算，在第二颗星伪距上加入0.5m 固定偏差，仿真200次，统计与真实位置之间的经度、纬度和高程误差，结果见图3。

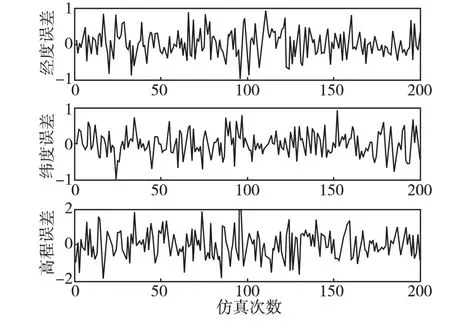
图3 存在故障星时的定位精度Fig.3 Positioning accuracy with one faulty star

第二颗卫星不参与定位解算，利用剩下的8颗星进行定位解算，仿真200次，统计与真实位置之间的经度、纬度和高程误差，结果见图4。

图4 剔除故障星后的定位精度Fig.4 Positioning accuracy without faulty star

在仿真中采用同样的9颗卫星，产生的模拟伪距和模拟钟差，可以认为在这个过程中卫星的位置是不变的，也就排除了GDOP或卫星自身精度较差的原因而导致两者定位精度差异。从图3和图4定位解算的高程误差均高于经度和纬度误差，这是因为GPS对高程定位精度相对较差。对比图3和图4可以发现，在剔除故障星后定位解算的经度、纬度和高程误差幅值减小为原来的一半，这说明存在较小伪距偏差的卫星参与定位，并没有因为卫星数目增加了一颗提升定位精度，反而使定位精度明显下降。这就对针对较小伪距偏差的RAIM 监测可靠性提出了需求。

3.2 单颗卫星出现故障

在3号星伪距上加入一定偏差，采用单历元积累值，分别求矩阵RN的1～9 列向量与第10列向量之间的夹角余弦和相关距离。

表1中10m 偏差，3号星夹角余弦和归一化相关距离分别为0.92和0.36，夹角余弦明显大于其他星，而相关距离又明显小于其他星，说明二者一致反映3号星即为故障星。0.45 m 偏差的夹角余弦最大值7号星的0.79，相关距离最小值为9号星的0.82，两者结果不一致，且各检测量之间差别不大，这说明在伪距出现0.45 m 的偏差时，单历元叠加无法分辨出故障星。

在3号星伪距上加入一定偏差，采用10历元积累值，分别求矩阵RN的1～9 列向量与第10列向量之间的夹角余弦和相关距离。表2 中10m 偏差和0.45m 偏差，采用10叠加，夹角余弦和归一化相关距离均一致，可以分辨出故障星，这也验证了归一化相关距离多历元累加法的可行性。

表1 单历元检测量Tab.1 Detectable quantity with one epoch

表2 10历元累加检测量Tab.2 Detectable quantity with ten epoch

3.3 单星和双星故障检测概率统计

采用归一化向量相关距离法进行RAIM 检测，在8颗卫星的伪距上每次随机的在其中一颗加入偏差，当检测出的故障星与已知一致即可认为RAIM成功，如此仿真1 000次，统计检测概率，见表3。

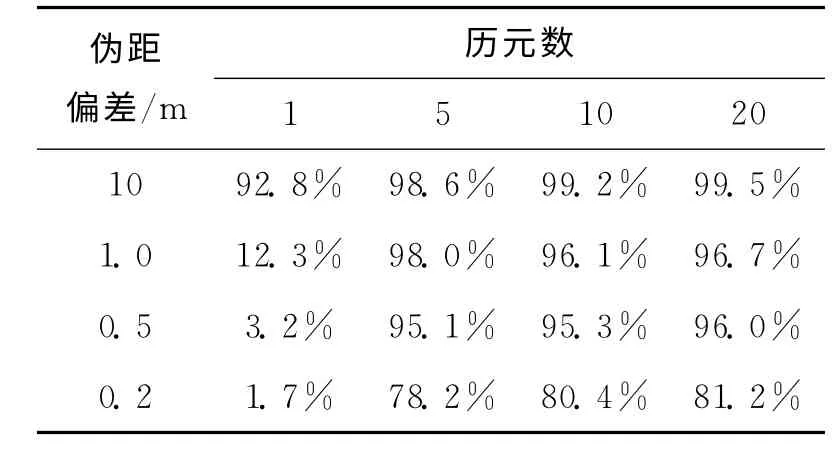
表3 单星故障多历元累加检测概率Tab.3 Detection probability of several epoch accumulative with single faulty star

采用归一化向量相关距离法进行RAIM 检测，在8颗卫星的伪距上每次随机的在其中两颗加入偏差，当检测出的故障星与已知一致即可认为RAIM成功，如此仿真1 000次，统计检测概率，见表4。

表4 双星故障多历元累加检测概率Tab.4 Detection probability of several epoch accumulative with two faulty stars

表3中10m 偏差随着历元的增加变化不大，1.0 m 及其以下采用单历元法检测概率在15%以下；而5、10、20历元累加归一化相关距离法检测概率远高于单历元的，随着积累历元的增加，检测概率增大。表4与表3反映的情况一致，对比表3和表4，双星故障RAIM 检测概率明显低于单星故障RAIM，这是因为当存在多个异常值时，由于粗差的相互作用有可能将没有粗差的卫星检测量拉偏而出现“弃真”，这就需要完善反向检查，尽量避免“弃真”的发生。

4 结论

本文利用噪声引起的伪距残余的随机性得到一种改进后的基于多历元相关距离的RAIM 算法，该方法通过构造奇偶矢量多历元叠加矩阵，将N 个历元的伪距信息进行整合，其中的固定偏差量得到累积，而由噪声引起的偏差互相抵消，然后用归一化相关距离检测出存在故障的卫星。该方法可以有效检测存在多异常值慢变伪距偏差的情况，仿真部分采用BDS／GPS组合导航接收机的9颗卫星进行仿真，验证了该方法的可行性，并与传统单历元方法进行了对比，结果表明，该方法可有效检测静态和低动态条件下存在微小伪距偏差的情况，单星存在0.5m 偏差时，检测概率提高到95%以上，双星存在0.5 m以内偏差也可以提高到60%以上。

［1］张强，张晓林，常啸鸣.用于识别两颗故障卫星的RAIM算法［J］.北京航空航天大学学报，2008，34（7）：773-777.

［2］赵琳，李亮，程建华，等.用于识别双星故障的RAIM 算法［J］.北 京 航 空 航 天 大 学 学 报，2010，36（11）：1262-1265.

［3］秘金钟，谷守周，方书山 .基于向量相关距离的新型RAIM 算法［J］.中国科学，2010，40（5）：638-643.

［4］刘文祥.卫星导航系统高精度处理与完好性监测技术研究［D］.北京：国防科技大学，2011.

［5］谢钢.GPS原理与接收机设计［M］.北京：电子工业出版社，2009.

［6］任锴，杨力，赵庆海.QUAD 方法用于RAIM 故障检测术［J］.大地测量与地球动力学，2009，29（5）：125-128.

［7］王永超，黄智刚.时钟改进模型辅助RAIM 算法研究［J］.电子学报，2007，35（6）：1084-1088.