Excel表格在土的液塑限试验数据处理中的应用
2014-01-12赵翔宇
赵翔宇
(山西省交通科学研究院,山西 太原 030006)
土的液塑限是划分土的分类和计算土的天然稠度及塑性指数的依据,是施工和设计的重要指标。液塑限指标计算的准确性关系到土壤定名的正确性,同时液塑限的大小也反映了土粒之间联结强度随含水量变化的性质,反映了土在不同含水量状态下对外力引起变形或破坏的抵抗能力。塑性指数是反映黏性土可塑性的指标,是反映黏性土中黏粒和胶粒含量的重要指标,可用于黏性土的分类和命名;而液性指数亦反映出天然土的干湿程度或软硬程度,更好地评价土的各项物理性能,因此准确地测定和计算土的液塑限对工程的设计和施工有重要意义。
1 液限和塑限联合测定法介绍
按照《公路土工试验规程》(JTG E40—2007)中T0118—2007《液限和塑限联合测定法》,测定方法介绍如下(以100 g锥为例):
a)取0.5 mm筛下的风干代表性土样 200 g 3份,分开放入3个盛土皿中,加入不同数量的蒸馏水,土样的含水率分别控制在液限a点(锥入深度20 mm±0.2 mm)、略大于塑限的c点(锥入深度小于5 mm)和二者中间状态b点,用调土刀调匀,盖上湿布放置18 h以上。
b)将制备的土样充分搅拌均匀,分层装入盛土杯中,用力压密,使空气逸出。对于较干土样,应先充分搓揉,有调土刀反复压实。试杯装满后,刮成与杯边齐平。
c)接通电源,调平机身,打开开关,提起锥体(此时显示为零),锥头涂少许凡士林。将装好土样的试杯放在联合仪的升降座上,转动升降旋钮,试杯徐徐上升,待锥尖与土样表面刚好接触时指示灯亮,停止转动旋钮,锥体立刻自行下沉,5 s时自动停止下落,显示锥入深度h1。
d)改变锥尖与土的接触位置(锥尖两次锥入位置距离不小于1 cm),再次测定锥入深度h2。h1、h2允许平行误差为0.5 mm,否则重作。取h1、h2的平均值为该点的锥入深度h。
e)去掉锥尖入土处的凡士林,取10 g以上的土样两份,分别测定其含水率w1和w2(精确到0.1%),计算含水率的平均值w。
f)重复b~e步骤,对其他两份含水率土样进行试验,测其锥入深度和含水率。
按照规程得出一组土样的数据(见表1)。
2 按照试验规程中数据处理方法
在双对数坐标纸上,以含水率w为横坐标,锥入深度h为纵坐标,点绘a、b、c3点含水率的h-w图,连接此3点,应呈一条直线。如3点不在同一直线上,要通过a点与b、c两点连成两条直线,根据液限(即a点含水率)在hP-wL图上查得hP,以此hP再在h-w的ab及ac两直线上求出相应的两个含水率。当两个含水率的差值小于2%时,以该两点含水率的平均值与a点连成一直线。当两个含水率的差值不小于2%时,应重做试验。
在h-w图上查得入土深度h=20 mm所对应横坐标的含水率w,即为该土样的液限wL。
3 传统数据处理
a)绘制双对数坐标。以含水率w为横坐标,取长度10 cm代表起点10%~终点70%,以锥入深度h为纵坐标,取长度10cm代表起点1mm~终点30mm。
b)点绘 a点坐标(27.3,20.1),b 点坐标(19.5,9.9),c 点坐标(13.2,4.2)
以 a点坐标(27.3,20.1)为例计算。

c)考查 a、b、c3 点是否在同一直线上,即 ab 及ac两条直线的斜率是否相同:

d)根据a点含水率27.3%在hP-wL图上根据土的类别采用不同计算公式得到:
hP=29.6-1.22wL+0.017wL2-0.000 074 4wL3=7.450 mm.

e)计算纵坐标对应ab及ac两条直线方程、对应横坐标及含水率
ab 直 线 方 程 为 :y=1.204x+2.608,xHp1=(5.904-2.608)/1.204=2.738,反算含水率w1=17.0%.
ac 直 线 方 程 为 :y=1.233x+2.461,xHp1=(5.904-2.461)/1.233=2.794,w2=17.2%.
含水率之差小于2%,可以取w1和w2平均值w=17.1%,hP=7.45 mm.
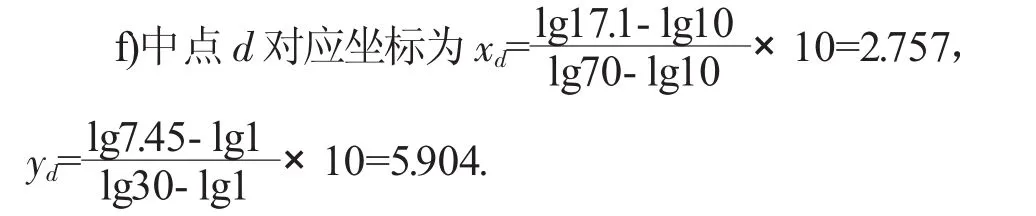
直线ad方程为:y=1.214x+2.558.
h)根据 wL由 hP-wL图计算得:hP=29.6-1.22wL+0.017wL2-0.000 074 4wL3=7.48 mm,
再由h-w图中直线ad上计算出对应含水率即为塑限:wP=17.2%.
经过以上计算得出:wL=27.2%,wP=17.2%,IP=10.0%.
4 运用Excel表格处理数据
a)新建一个 Excel表格(如表2),第 2列第 C、D、E行输入a、b、c 3点含水率,第3列输入对应锥入深度值,第4列和第5列计算对应的对数坐标值x和y(此时可用10 cm代表横坐标含水率10%~100%,用10 cm代表纵坐标锥入深度1~30 mm,用来验证与手工计算结果的一致性)(见表2)。

表2 液塑限计算表

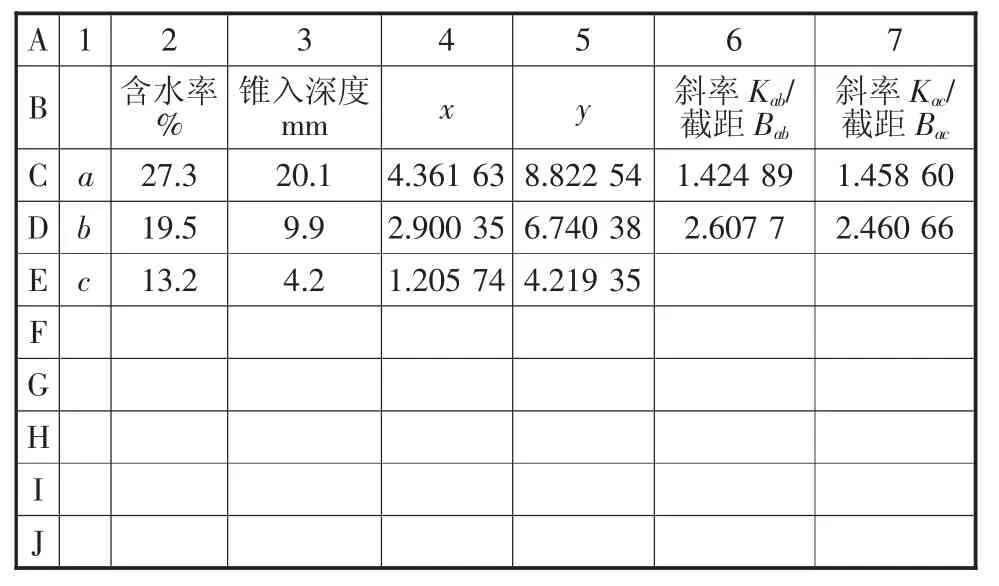
表3 液塑限计算表
计算两直线方程截距并得出方程:
Bab=ya-Kab×xa=yb-Kab×xb=2.607 701,ab方程:y=1.424 89x+2.607 701.
Bac=ya-Kac×xa=yc-Kac×xc=2.460 665,ac 方程:y=1.458 60x+2.460 665.
c)根据a点含水率在hP-wL图上用公式计算对应的 hP,
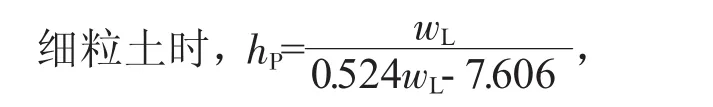
砂类土时,hP=29.6-1.22wL+0.017wL2-0.000 074 4wL3=7.450 157 mm.
d)在表4中F、G行的第 2、3、4、5 列分别计算 hP在直线ab、ac上对应点的纵、横坐标和含水率。
第4列F、G行计算对应直线ab、ac上的横坐标:
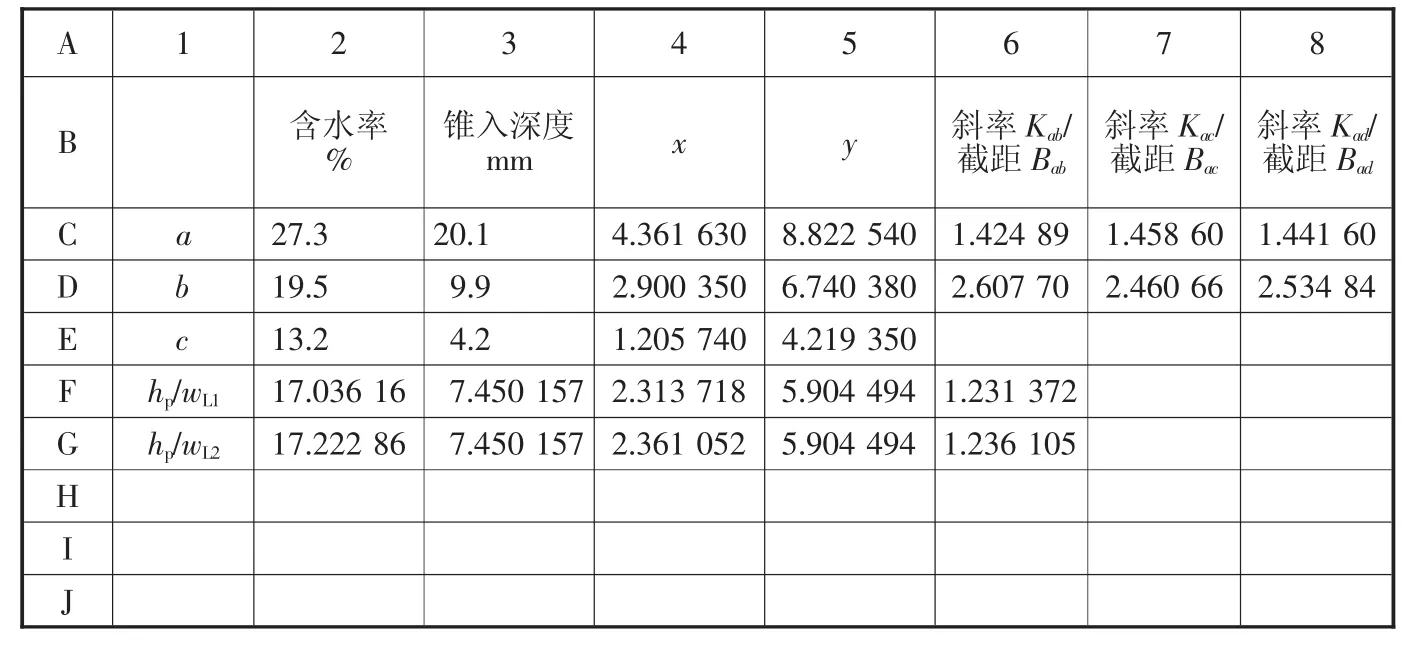
表4 液塑限计算表

第2列第F、G行反算含水率:

w1=101.231372=17.036 16%,同样计算出w2=17.222 86%.
e)在表5中第2列第H行格中插入条件函数“IF
(ABS(F4-G4)<2,(F4+G4)/2,"false")判断 w1和 w2相差是否小于2%,如果小于2%,可以计算平均值w=17.129 51%,hP=7.450 157mm,即 d点的值,然后计算d点坐标和直线ad方程:y=1.441 596x+2.534 837;否则输出“false”,重做试验(见表5)。

表5 液塑限计算表
f)第I行由锥入深度h=20 mm计算出在直线ad上对应的纵坐标和横坐标(即wL点):

得出含水率wL=27.236 13%≌27.2%即为液限。
g)根据液限 wL在 hP-wL图上计算 hP=29.6-1.22×wL+0.017×wL2-0.000 074 4×wL3=7.479 462 mm,再由h-w图中直线ad上计算出对应含水率即为塑限wP=17.2%,对应点wP(第J行数据)。
h)经过以上所以得出结论:wL=27.2%,wP=17.2%,IP=10.1%(数据保留一位小数)。结论与手工计算相同,表格中只要更改初始试验数据a、b、c3点锥入深度和含水率,即可方便计算出结果。
5 结论
通过以上两种计算方法的对比可以看出,手工计算每次数据不同时需要重新计算,数据计算量大且精度不高。运用Excel表格编写好公式后,只要更改初始试验数据即可直接得出结论,大大地方便了数据处理,减轻了手工计算工作量,提高了精度,并且可以利用Excel图表功能绘制出双对数坐标图,准确清晰地得出试验结论,在工程实践中得到了良好的应用。
