表面波检测的数值模拟与试验对比

王 贝，窦晓兰，韩晓华

（1.山东省科学院激光研究所，济宁 272017；2.山东省济宁市粮食局，济宁 272019）

为获得工件的超声波检测图像，按照检测的步骤，要先制定检测工艺方案，再制备对比试块，准备仪器和换能器，这一过程不可避免地耗费着大量的人力物力。另外，对于结构复杂工件的检测结果，还需要有经验的技术人员做出判定。而借助于有限元数值模拟可以弥补上述的不足，其能够进行纵波、横波、兰姆波等超声波声场的仿真，可直观形象地呈现超声波在工件中的传播过程，并根据需要进行再现。在声场模拟计算方面，有学者做过一定的工作：宗侣等利用ANSYS软件模拟了导波在管材中的传播［1］；刚铁等利用MARC 模拟计算了Lamb波在薄板中的传播［2］；孙继华 等［3］及刘长福等［4］进行了纵波及横波的有限元模拟计算方面的工作。然而对于表面波检测，尤其是遇到缺陷后所发生的波型转换现象，相关的有限元分析工作较少。笔者以无损检测中经常使用的1.5 MHz表面波探头为例，运用斜楔纵波入射在界面处获得表面波的原理，对表面波的传播过程进行了有限元分析。

1 理论模型

表面波在介质表面传播时，介质表面质点作椭圆运动，可等效为质点纵向与横向振动的合成。纵波折射法表面波换能器的原理如下：压电晶片产生的纵波通过不同倾角的斜楔射向试件表面，经波型转换可在试件中相应地产生表面波，斜楔一般用有机玻璃制作［5］。图1所示为表面波探头压电晶片和斜楔的二维结构简图，介质1为有机玻璃，介质2为被检测工件。有机玻璃／工件界面上波的入射范围为AB，纵波的入射角为αL，当入射角大于第二临界角时，工件中无纵波和横波出现，经波型转换后仅在界面上形成表面波，斜楔中纵波的速度为CL，工件中表面波的波速为CR。

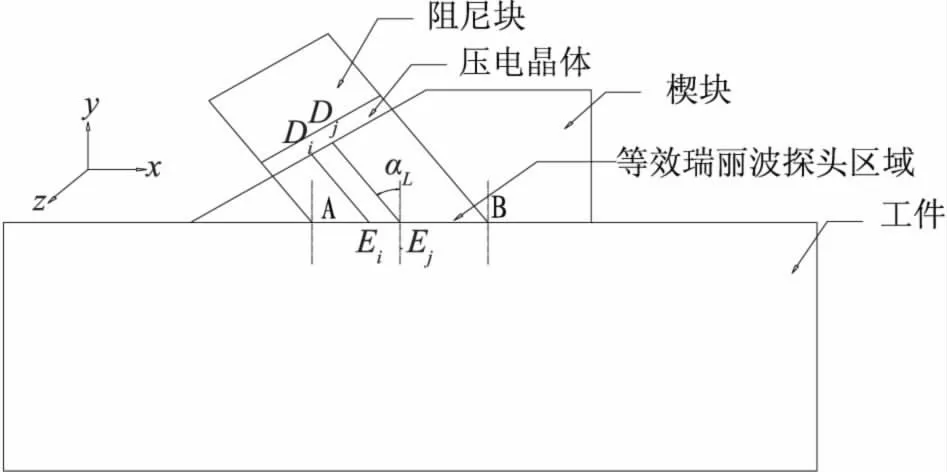
图1 工件表面等效为表面波换能器的原理

设Di、Ei、Dj、Ej为介质1 中任意两条波线 上的点，压电晶片产生的同相位纵波分别沿波线DiEi与波线DjEj传播到界面上Fi与Fj，相对应的时间分别为Ti与Tj，关系为：

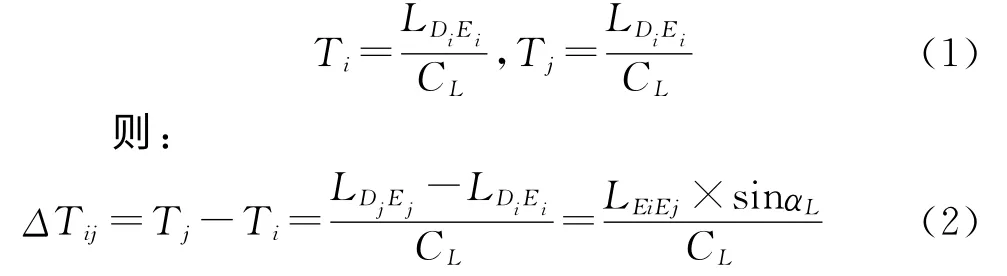
式（2）说明同相位的纵波由压电晶片发出，沿不同波线到达BC 上各点具有一定的时间差。于是，在进行数值模拟时，为了简化模型，可以去除斜楔和介质1中的压电晶片，只考虑介质2工件，将工件的AB区域等效看为表面波换能器压电晶体激励表面，那么界面上的各振点之间应该存在着对应于时间差ΔTi，j的相位差。

AB区域中各振点的激励力方向也是一个很重要的因素，实际超声波无损检测过程中，由于介质1中表面波探头和介质2之间存在着液体耦合剂，因为耦合剂属于液态物质，不能传递切向力，所以激励力的方向应该平行于介质2表面法线的方向［6］。因此在有限元分析过程中，激励信号施加的方向应该与工件表面垂直，另外为了避免边界反射造成影响，将两侧边界设置为吸收边界［7］。

2 数值计算与分析

2.1 材料属性参数

假设选取的工件材料内部的力学性能是各向同性的，工件材料为钢。另外计算时有机玻璃中纵波的速度为2 700m／s。同时钢中纵波的速度为5 940m／s，横波速度为3 290m／s，表面波速度为3 041m／s。工件的力学性能参数分别为：弹性模量为2.16×1011Pa；泊松比为0.28；密度为7 800kg·m－3。

2.2 有限元模型

工件的整体尺寸为50mm×20mm（长×高），加载区域的中心处于上表面距左侧10mm 的位置，加载区域的宽度为10 mm。缺陷中心距工件左侧25mm，缺陷尺寸为1 mm×5mm（宽×深）。有两种建立缺陷工件模型的方法：一种是直接创建带有缺陷的工件，然后进行网格划分；另一种是先建立完整的工件，进行网格划分后，利用单元生死技术将缺陷处的单元杀死。为了便于线性计算和控制计算时间步长，选用第一种方法生成工件模型。根据超声换能器产生激励信号的形式，在加载区域内施加的力［8］为式（3），力的单位为N，时域函数图形与频谱图如图2所示。

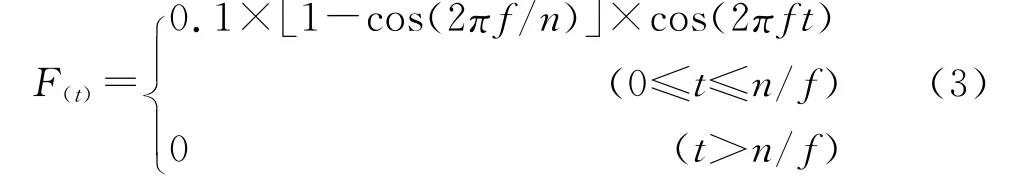
式中：f为激励信号 的中心 频率1.5 MHz，；n为周期数。取n＝3。

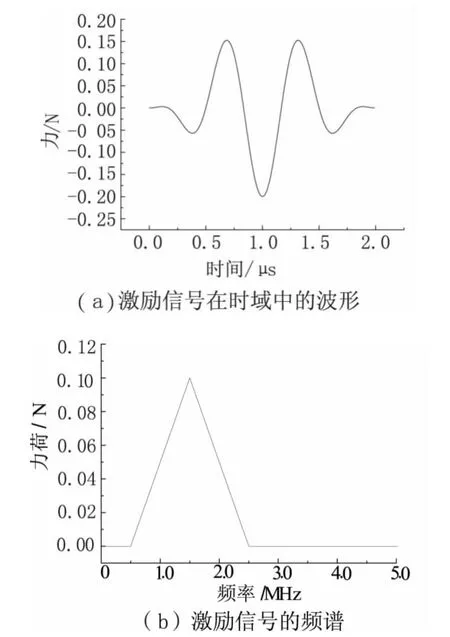
图2 激励信号的时域波形与频谱图

选取4个节点的2维结构单元划分工件，每个节点各有两个自由度，在缺陷周围的区域，将4节点结构单元退化为3节点结构单元，可以将模型划分的更加有规律些。为满足描述工件中弹性表面波传播的精度要求，网格的大小按式（4）进行选取［9－10］。

式中：λmin为计算时所关注的最小波长。

根据表面波速度及中心频率，可计算出：

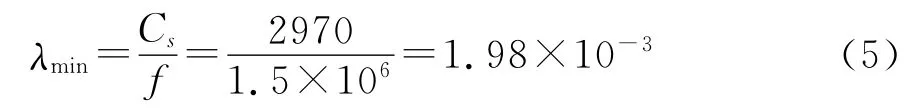
则Δl可取为2×10－4m。

吸收边界采用粘弹性人工边界的形式，可等效为连续分布的并联弹簧－阻尼器系统，人工边界上法向和切向的单元同时具有弹簧刚度和阻尼系数，在此选取2维弹簧—阻尼器单元。根据以上数据建立的有限元模型如图3所示。

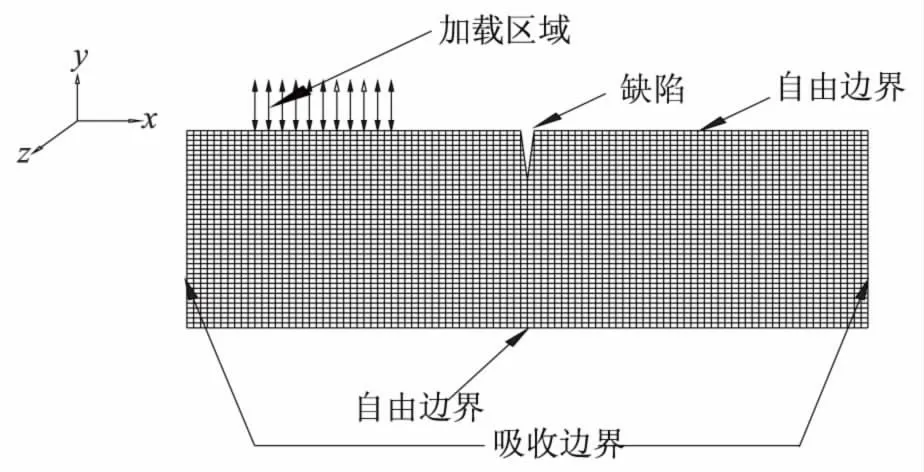
图3 有限元模型

2.3 载荷加载激励与求解

为了确定系统在瞬态载荷作用下位移、应力、应变、力随时间变化的规律，即系统的结构动力学响应，应当选用瞬态动力学分析（时间历程分析）。结构的动力响应可以看作是各阶模态响应的组合，积分步长Δt应小到能够解出对结构整体响应有贡献的最高阶模态，设fmax为结构响应的最高阶频率（Hz），则积分步长应为：

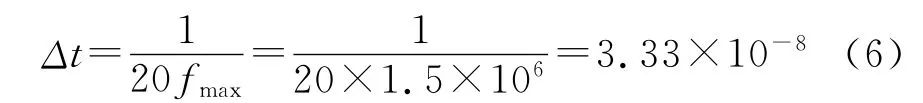
为了产生表面波，对于式（3）所描述的激励信号，加载区域内各节点的起振时刻需要有一定的时间差，在程序中首先根据式（2）计算好每个节点各自的延迟时间，然后按照时序与加载节点的先后顺序对加载区域中每个节点进行力的加载。节点力加载完毕后，进行求解和数据处理。

2.4 结果分析与试验

为了便于描述，将带有缺陷的工件标记为工件A，对A 进行有限元分析。首先说明表面波未到达缺陷前的速度，对于工件A，在上表面处距离左侧16，21，36，44 mm 处分别取四个不同的节点AA、BA、CA、DA，下标表示节点属于工件A，显然AA、BA处于缺陷左侧而CA、DA处于缺陷右侧。提取AA、BA两个节点位移的时间历程数据，绘制曲线，如图4（a）所示，实线矩形框中为直通表面波信号，虚线为反射波信号。根据直通波两波峰之间的时间差Δt1＝1.62μs以及两节点间距Δs＝5mm，计算出表面波的速度为3 082.8m／s，与理论速度3 041m／s之间的相对误差为1.37%，可见有限元方法计算出来的表面波速度与理论速度相符。同理，求出反射波的速度同样为3 082.8m／s，该反射波仍为表面波，可以说明：一部分表面波信号在裂纹开口处仍以表面波的形式被反射，并沿物体表面的原路径返回。

其次，说明表面波遇到缺陷时，会沿裂纹表面传播，并在经过裂纹后，仍能够以表面波的形式沿工件表面继续传播。图4（b）为CA、DA两点位移的时间历程曲线，按照上述求解速度的方法，计算出波的传播速度为3 098.4m／s，与表面波理论速度之间的相对误差为1.89%，说明该信号仍为表面波，因此所述的观点能够得以验证。另外可利用CA、DA两节点的起振时刻与无缺陷时的起振时刻之间的差值，估算出缺陷尺寸。

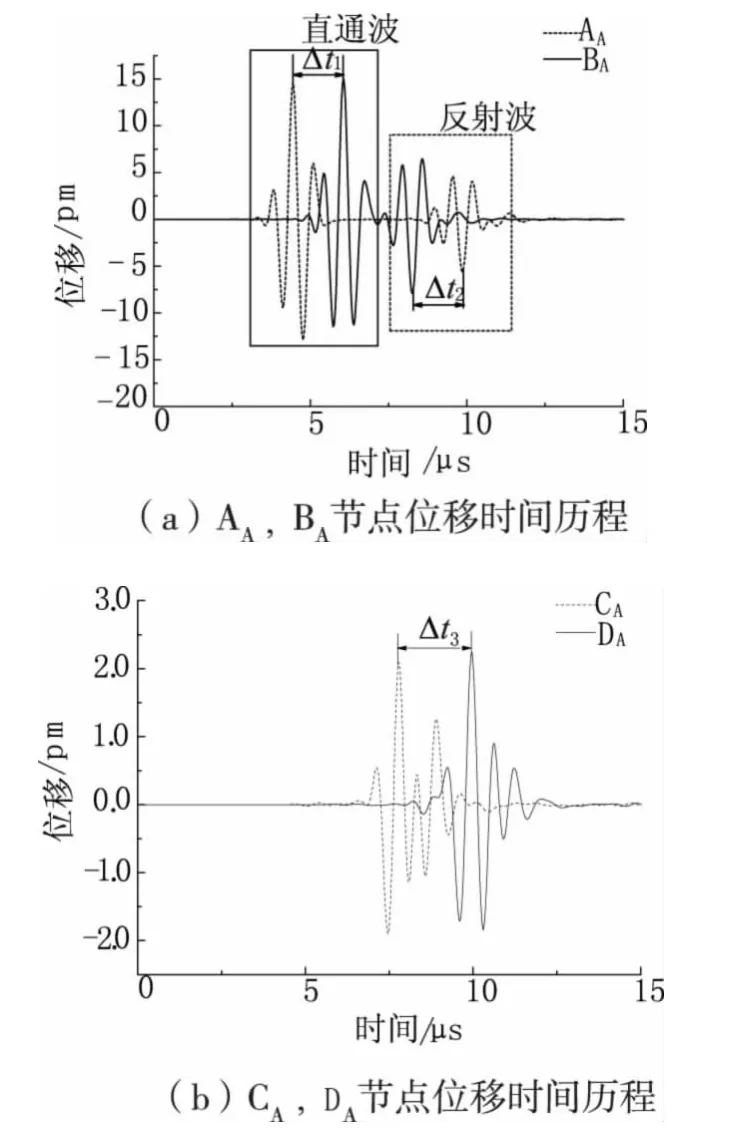
图4 工件A 上表面节点位移的时间历程曲线

图5中为工件A 不同时刻的波场快照图片，图5（a）为5.28μs时刻的波场快照，此时R1表面波未到达缺陷；图5（b）为10.4μs时刻的波场快照，显示了表面波遇到缺陷后声场发生改变的状况。根据上述声速计算可知，R2为遇到缺陷反射回来的表面波，R3为经过缺陷而继续传播的表面波。对于信号波S1，S2，S3，L1，需要计算出波的传播速度以确定波的类型。具体实现过程是，在不同时刻，分别取出相应信号波传播路径中位移最大值对应的节点，这些节点即是处于声束轴线上的点，根据节点坐标便可以求出节点间距，结合时间差，求出多个速度值然后取平均。将所获取的信号波速度列于表1，其中S1，S2，S3的速度均与横波理论速度相吻合，L1的速度与纵波速度相吻合。说明表面波在遇到缺陷时发生了波型转换，转换为变形纵波和变形横波，在工件内部传播。

图5 工件A 的声场快照

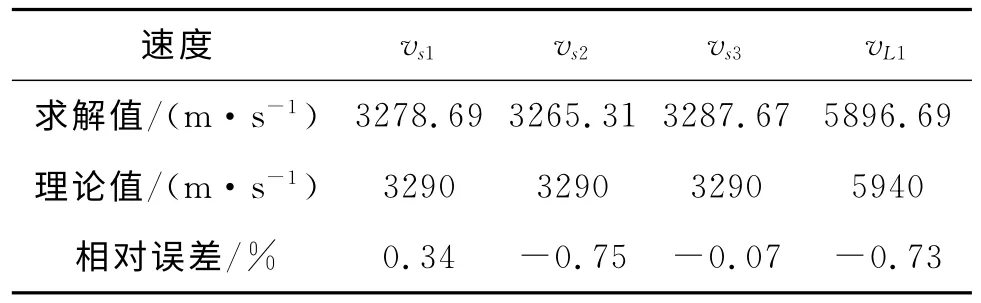
表1 信号波速度的仿真求解值与理论值

通过试验的方式对上述有限元分析结果进行说明，为了便于固定探头和分析试验结果，采用290mm×290mm×60mm 的45钢工件。表面波发生波型转换后的各类型波具有一定的指向性，即声束轴线的角度一定，实际工件和有限元模型尺寸上有差别，厚度尺寸比例系数为3，根据比例系数求出表面波探头与缺陷的距离为45 mm。采用汉威HS616e型便携式探伤仪和1.5 MHz的表面波探头激发表面波。使用型号TDS 2024C 的泰克示波器接收压电探头输出的信号，主要参数为带宽200 MHz，采样频率2GS／s，为了去除噪声干扰，对采集到的信号进行8次平均。另外为了接受纵波和横波，还使用了中心频率均为1.5MHz的纵波探头和K1.5横波探头，图6为试验方案，图中矩形为表面波激励探头，圆形A、B、C、D 四点表示为信号接收探头的位置，PR 为表面波探头，PL 为纵波探头，PS为横波探头。根据探头距缺陷的距离和表面波速度，计算出表面波到达缺陷所用时间为TR＝14.8μs。

图7（a）所示表面波到达D 处的时刻为TD＝29.6μs，与TR的差值为14.8μs，乘以表面波的速度，得到相应波程为45mm，又因为D 点距表面裂纹42mm，因此可估算出工件表面裂纹的纵向尺寸为1.5mm。图7（b）为B、C 处横波探头接收的信号，读取试验数据知TB＝36.6μs，TC＝50.6μs，与TR的差值即为横波传播所需的时间，结合B、C两点缺陷的距离，可求出波速分别为3 303 m／s、3 296m／s，均与横波速度吻合。图7（c）为A 处探头接收到的信号，从图中得出TA＝38.2μs，按照上述方法计算出从缺陷处传播至A 处的波速度，其数值为5 983m／s，与纵波速度值相符。

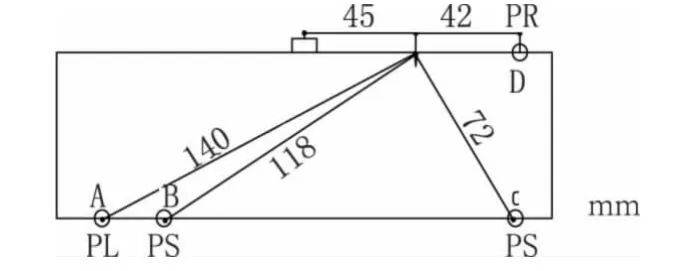
图6 试验方案

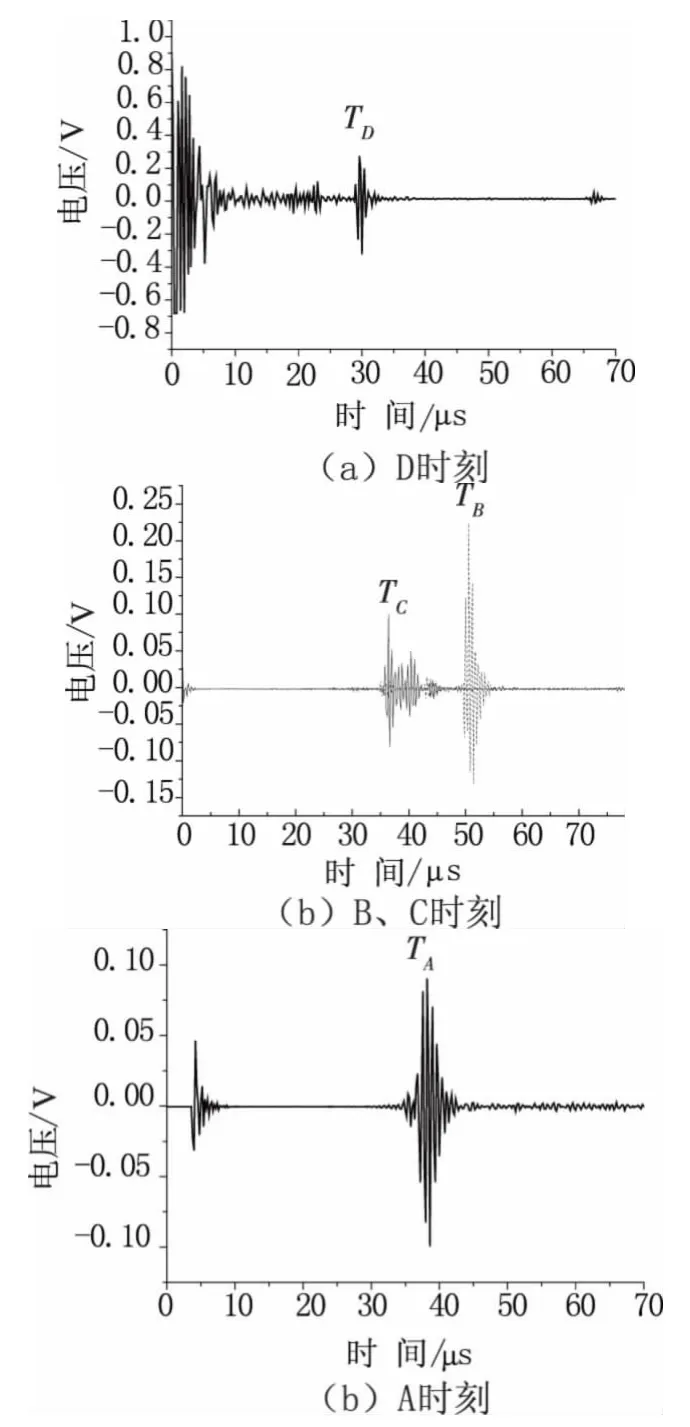
图7 各探头接收的信号

通过上述对比试验和分析可知，根据得出的速度数据，确定信号波的类型，进而推断出表面波遇到缺陷后整个声场的状况：声场中除了含有沿着缺陷并继续传播的表面波外，还会生成纵波和横波，这与有限元分析结果相一致。

3 结论

提出了等效表面波换能器有限元模型，实现了工件表面波检测的有限元分析，并利用试验进行了分析。数值计算获得的表面波、横波及纵波的速度均与理论值相符合。表面波遇到缺陷时一部分仍继续传播，另外发生的反射、波型转换等，均能够通过有限元模拟计算出来。利用有限元分析可以对工件检测进行结果预测和评估，能够为超声波检测提供参考和对比。并且相对于理论分析，有限元分析更加直观方便。

［1］宗侣，王悦民，朱龙翔.超声导波在弯管中传播特性的有限元分析［J］.无损检测，2013，35（11）：43－46.

［2］刚铁，刘强.薄板结构中Lamb波的检测与仿真［J］.无损检测，2013，35（7）：24－28.

［3］孙继华，李书光，倪云鹿，等.固体中缺陷对声波频谱特性影响的有限元仿真［J］.计算机仿真，2008，25（8）：308－311.

［4］刘长福，牛晓光，李中伟，等.基于ANSYS 的超声纵／横波传播仿真计算［J］.无损检测，2011，33（6）：5－18.

［5］郑辉，林树青.第2版：超声检测［M］.北京：中国劳动社会保障出版社，2008.

［6］JASIUNIENE E，ZUKAUSKAS E.The ultrasonic wave interaction with porosity defects in welded rail head［J］.Ultragarsas，2010，65（1）：12－18.

［7］李书光，孙继华，李树榜，等.孔洞对透射波频谱影响的有限元数值模拟［J］.无损检测，2009，31（1）：72－75.

［8］BASKARAN G，RAO C L，BALASUBRAMANIAM K.Simulation of the TOFD technique using the finite element method［J］.Insight－Non－Destructive Testing and Condition Monitoring，2007，49（11）：641－646.

［9］NANDY A，MULLICK S，De S，et al.Numerical simulation of ultrasonic wave propagation in flawed domain［C］／／［s.l］：NDE，2009：160－163.

［10］GHOSE B，BALASUBRAMANIAM K，KRISHNAMURTHY C V，et al.Two dimensional FEM simulation of ultrasonic wave propagation in isotropic Solid Media using COMSOL［C］／／India：COMSOL Conference，2010.