折面梁格法在宽箱连续梁受力分析上的应用
2014-01-09梁维全
梁维全
(上海市政交通设计研究院有限公司,上海市 200030)
0 引言
经济的发展带动交通现代化的建设,城市桥梁横向宽度不断增加。在这种情况下,国内外建造预应力混凝土桥梁时多采用大悬臂单箱多室宽箱截面形式[1]。这种桥梁具有腹板间距大、横向翼缘宽、箱壁薄等特点[2]。在结构设计时,正确分析薄壁单箱多室宽箱断面结构的力学行为是桥梁设计的难点和重点。由于宽箱结构的复杂性,以及荷载的多样性,实际工程设计过程中很少直接用实体单元或板壳单元进行空间分析,而是将桥梁转化为平面梁系,梁格或单梁进行结构内力和位移的计算,这就涉及复杂空间结构的简化问题,也就是实用计算方法的问题。要寻找空间结构的实用计算方法,就必须深入分析结构的受力特点,以便使实用计算方法能充分体现出结构的受力特点,以保证结构设计偏于安全。因此有必要进一步的探索和研究一种适合单箱多室宽箱梁的实用计算方法[3]。
在实际工程设计中,现有的桥梁结构空间分析方法主要包括考虑空间效应的单梁法、梁格法、网格法、框架简化计算法及实体有限元法。针对单箱多室宽箱梁的受力特点,以梁格法为基础,提出一种折面梁格法:将截面以沿垂直于截面主轴方向的切割线切开,保持各纵向梁格的形心位置不变,并采用横向梁格将各纵向梁格联系在一起,结合修正后的纵向、横向梁格的截面特性形成一个单层的折面格构式计算模型,计算结果采用“阶梯”型的正应力分布模拟连续的正应力分布,如图1所示。折面梁格法有限元模型适合于具有多道腹板的宽箱梁整体分析,其优点是可以将纵梁和横梁放在一个模型中进行计算,并可以反应自重、预应力,以及其他外部荷载下剪力滞效应和偏载作用下各道腹板的横向分配。

图1 梁格模型计算正应力阶梯表达形式示意图
以某城市快速路高架桥梁单箱多室宽箱连续梁为例,分别建立了平面杆系、三维实体有限元和折面梁格法分析模型。首先分析了这种宽箱截面正应力分布,然后对比了三种模型计算结果,验证了折面梁格法的有效性,对类似单箱多室宽箱截面应力验算分析提供了一种可靠方法。
1 工程实例
某城市桥梁采用跨径组成为3×30 m跨径的单箱五室预应力混凝土等高度连续梁结构形式,桥面宽25.24 m,宽跨比0.84,为典型的宽箱结构。
箱梁截面为单箱五室截面,设有6道腹板,箱梁顶板水平长25.24 m,底板水平长18.47 m,悬臂板长2.87 m,悬臂板与腹板之间采用圆弧曲线过渡。桥面中心线处梁高为2 m,顶底板处均设置2%横坡。箱梁顶板厚20~22 cm,底板厚22~40 cm,腹板厚40~60 cm。在桥墩处设置横梁,中横梁厚2 m,端横梁厚1.5 m。具体断面详见图2所示。
主要技术标准如下:
(1)材料取用:采用C50混凝土,弹性模量为 3 .45×104MPa;

图2 工程实体典型断面图(单位:mm)
(2)设计活载:为城市-A级(双向6车道);
(3)桥梁设计基准期:100 a;
(4)设计安全等级:一级。
2 宽箱截面受力计算方法
为验证折面梁格法在计算宽箱梁截面应力分布的准确性,分别建立了平面杆系、三维实体和折面梁格计算模型,进而对比分析三种方法在结构恒载作用下的计算结果。模型情况汇总如表1所列。
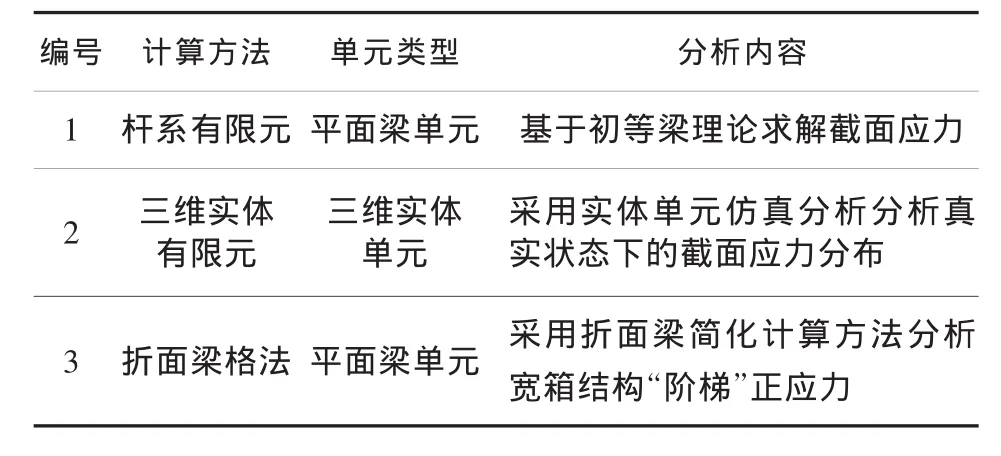
表1 模型情况汇总表
2.1 平面杆系有限元
基于平面杆系分析理论建立了工程实例的杆系有限元模型,如图3所示,通过求解截面受力,采用初等梁理论计算截面顶、底缘应力[4]。

图3 工程实例杆系计算模型
2.2 三维实体单元
三维实体单元仿真分析能够精确地计入宽箱截面的剪切、扭转、畸变及翘曲变形等,分析结果能够准确反应截面应力分布。本文采用大型通用有限元程序ABAQUS 6.12对工程实例进行三维实体有限元仿真分析,借助三维CAD软件PRO/E建立工程实例1/2几何模型,将其采用*.igs导入通用有限元程序ABAQUS中,三维实体有限元几何模型如图4、图5所示。通过ABAQUSCAE进行几何模型组装、网格划分及荷载的添加[5]。
三维实体单元采用C3D20R三维应力20节点减缩积分六面体等参单元,该类型单元具有较高计算精度。单元节点插值形式如图6所示,网格划分采用扫掠生成,局部网格划分如图7所示。

图4 实体单元几何模型(1/2模型)

图5 实体单元几何模型透视(1/2模型)

图6 20节点三维实体单元积分节点示意图

图7 三维实体单元局部网格划分图示
2.3 折面梁格法
折面梁格模型由6自由度梁单元组成,各纵横梁采用共用节点连接,纵向可依据单梁有限元划分方式划分,截面内部划分的疏密程度宜根据截面形式和计算要求确定,它反映了表达空间效应的精细化程度,折面梁格计算模型如图8所示。分割后的截面主要有腹板、二字型、翼缘板和工字型截面四种组成。本文将工程实体中的箱梁截面划分为20块,如图9所示。建立了分析单箱五室宽箱梁截面恒载作用下的空间力学行为,在求解单元内力按照单元刚度进行分配,计算结果采用“阶梯”型的正应力分布,模拟连续的正应力分布。

图8 折面梁网格计算模型
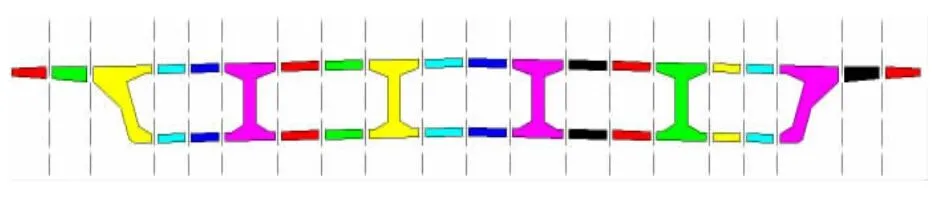
图9 采用划分20部分的宽箱梁截面示意图
3 对比分析
实体单元计算较为精确,能够反映宽箱梁截面真实应力分布状态,可作为理论值参考。通过折面梁格法、杆系有限元与实体有限元计算结果对比,分析单箱多室宽箱结构的截面正应力分布规律,并验证折面梁格计算结果的精度。
3.1 杆系有限元与实体单元结果对比
工程实例在恒载作用下的ABAQUS实体有限元仿真分析结果如图10、图11所示。
将实体有限元与杆系单梁模型计算所得恒载下边跨0.4L处的截面顶、底缘应力计算结果列于表2,并绘制顶、底缘应力横向分布示意如图12所示。

图10 恒载作用下结构整体正应力分布图(单位:MPa)

图11 边跨0.4L处截面正应力云图(单位:MPa)
由上述图表可知,对于截面顶缘应力,在悬臂板末端处压应力最小为1.92 MPa,中心处最大为3.18 MPa,悬臂板处应力水平明显小于其他位置顶板应力。悬臂段存在明显的剪力滞后效应,同时也说明了悬臂远端梁体参与纵向受力较低。对于截面底缘应力,在边腹板处拉应力最大为3.92 MPa,中心处最小为3.15 MPa。杆系单梁模型不能模拟单箱多室截面应力分布状况,需要通过其他方式计算截面剪力滞效应。
3.2 折面梁格与实体单元结果对比
将折面梁格与实体有限元计算所得恒载下边跨0.4 L处的截面顶、底缘应力计算结果列于表3,并绘制顶、底缘应力横向分布示意如图13所示。对比分析两者计算结果除2#、3#点外,折面梁格法计算结果与实体有限元计算结果相差在7%以内,说明折面梁格法在在计算单箱多室截面正应力分布具有足够的计算精度。

表2 杆系有限元和实体有限元恒载下截面正应力对比一览表(单位:MPa)

图12 实体单元和杆系有限元计算结果对比曲线图
4 结论
本文结合某城市3×30 m典型单箱五室宽箱连续梁桥,建立了杆系单梁、三维实体有限元和折面梁格法计算模型,分析宽箱截面正应力分布,通过对比分析三种方法计算结果可知:
(1)单箱多室宽箱梁结构在横断面上正应力分布具有明显不均匀性,剪力滞效应明显。
(2)采用折面梁格法计算可以得到与三维实体有限元分析较为吻合的结果,能够较为准确地模拟宽箱结构的力学行为,是一种较为可靠、实用的简化计算方法,可供设计人员参考使用。

图13 实体单元和折面梁格计算结果对比曲线图
(3)折面梁格模型不能反映截面顶、底板水平剪应力,无法校核顶、底板主拉应力,不推荐在薄壁效应较大的弯箱梁桥和较宽的单箱单室直线桥梁设计计算中采用。
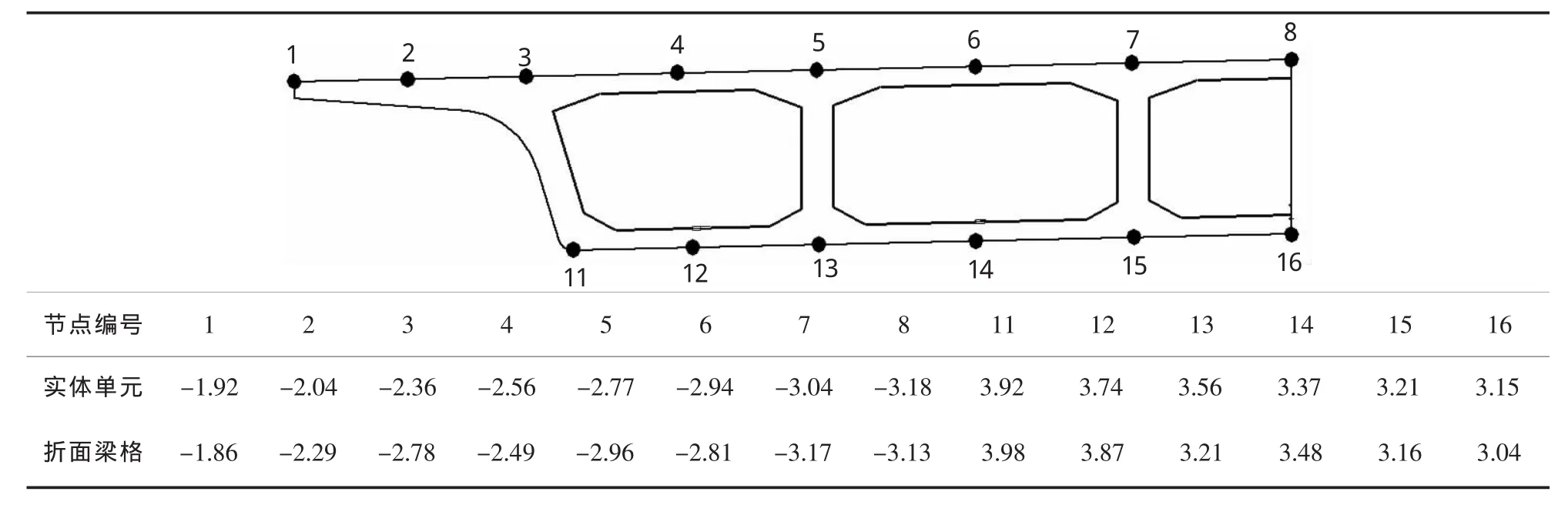
表3 折面梁格法和实体有限元恒载下截面正应力对比一览表 (单位:MPa)
[1] 徐海军,冷金荣.城市高架桥异形宽箱梁空间结构分析[J].结构工程师,2010,26(10).
[2] 曲慧明.宽箱梁剪力滞效应分[D].重庆:重庆交通学院,2003.
[3] 宋明曦.多室宽箱梁实用计算方法研究 [D].重庆:重庆交通大学,2013.
[4] 项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001.
[5] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006.
