阿什河哈尔滨城区段桥墩冲刷计算
2014-01-09毛倩倩李硕娇季永兴
毛倩倩,李硕娇,季永兴
(上海市水利工程设计研究院有限公司,上海市 200061)
0 引言
阿什河位于哈尔滨市东部,是松花江右岸的一级支流,干流河道长213 km,流域面积3 581 km2。阿什河下游哈尔滨市城区段约25 km,横跨香坊和道外两个区,其间有11座公路桥梁和1座跨河铁路桥梁。由于河道中设置了桥梁墩台,部分桥梁为减少投资而局部缩窄河道,使得桥梁位置河道过水断面缩窄,上下游水位差加大,流速加快,桥下河床冲刷严重,影响了河床稳定,并进一步影响桥梁安全。
桥梁墩台冲刷在冲积性河流中是无法避免的问题,是一个综合复杂的冲刷过程。桥梁墩台位置局部流速加大,墩台周围水流的边界层分离,从而产生高强度水流冲击和旋涡作用,使墩台附近河床产生冲刷,形成下切变形现象。当桥梁墩台周围冲刷坑深度较大时,会大大影响桥梁基础的稳定,威胁到桥梁自身的安全,需要进行桥梁防护。因此,桥墩冲刷计算就成了进行桥梁防护工程的首要任务。国内外学者通过物理模型试验、现场观测对桥梁冲刷的机理进行了分析研究,并通过实际测量及多变量分析等方法提出了一些桥墩冲刷计算方法[1]。
为向阿什河下游段河道整治建设部门提供桥梁位置合理过水断面,同时为桥梁防护提供可靠设计依据,笔者等人拟通过对国内外有关桥墩冲刷计算方法进行分析,结合实际工程选择可行性计算方法,并对哈尔滨阿什河城区段部分桥梁进行冲刷计算,为其桥墩防护工程提供科学依据。
1 国内外桥墩冲刷计算研究
在计算桥梁墩台冲刷时,应考虑桥孔压缩后河床断面内发生的一般冲刷、墩台周围水流结构发生急剧变化引起局部冲刷、河床自然演变冲刷等其他影响因素引起的冲刷。桥梁墩台冲刷深度的计算是对一般冲刷深度和局部冲刷深度进行计算,然后将两者结果叠加,作为桥梁墩台的最大冲刷深度计算值,以此来确定桥梁墩台防护工程的依据。
1.1 一般冲刷深度计算方法
(1)1964年,甘城道按照输沙平衡原理建立一般冲刷深度计算公式[2],即64-2公式:
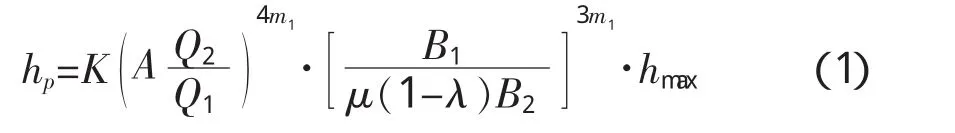
(2)由于64-2公式包含了变指数m1和变系数k,需要大量野外实测资料,计算较为复杂,因此公路桥位勘测设计规范推荐使用64-2简化公式[3]:
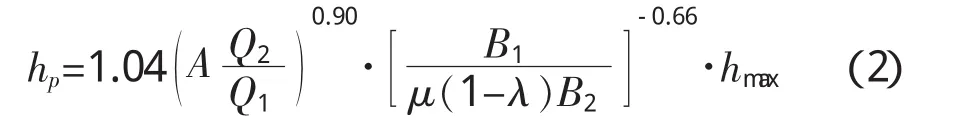
式中各参数意义见公式(1)中各参数意义。
(3)按冲止流速建立公式[4],则非粘性土河槽一般冲刷深度计算64-1公式为:
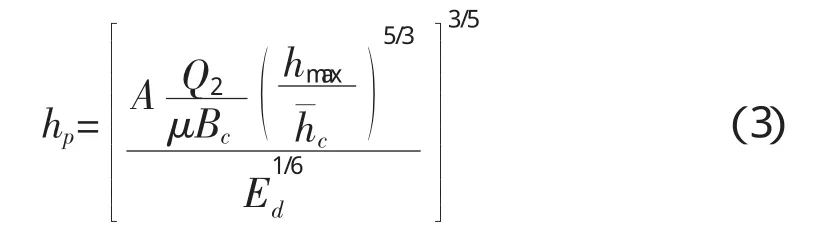
式中,Bc为河槽部分桥孔过水净宽,m;A为单宽流量集中系数;Q2为桥下河槽部分通过的设计流量,m3/s;为桥下河槽平均水深,m;hmax为设计断面上河槽最大水深,m;为河槽泥沙平均粒径,mm;E为与汛期含沙量的系数,S=(1~10)kg/m3时,E=0.66,S>(1~10)kg/m3时,E=0.86。
非粘性土河滩的一般冲刷计算64-1公式为:

式中,Q′t为桥下河滩部分通过的设计流量,m3/s;hmt为桥下河滩最大水深,m;为桥下河滩平均水深,m;B′t为桥下河滩部分桥孔过水净宽,m;vH1为河滩水深1 m时,非粘性土不冲刷流速,m/s。
(4)按冲止流速建立公式,则粘性土河床的桥下断面一般冲刷计算公式,河槽部分为:

式中,IL为冲刷范围内粘性土的液性指数,取值范围为0.16~1.19;其余参数意义见公式(3)各参数意义。
粘性土河滩部分一般冲刷公式为:
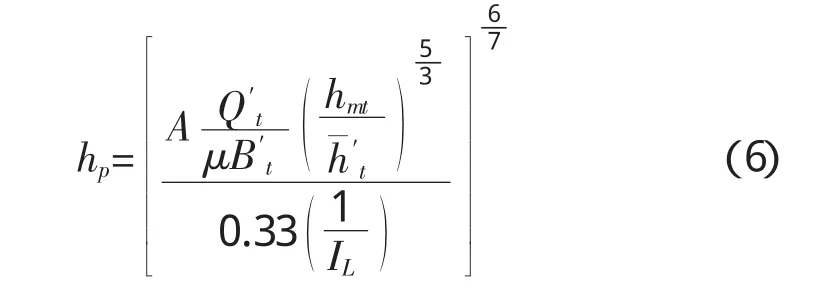
式中,各参数意义见公式(4)中各参数意义。
根据别列柳伯斯基的假定建立的公式[5]:
包尔达可夫根据别列柳伯斯基的假定,建立的桥下一般冲刷的经验公式,称为包尔达可夫公式,适用于稳定性河段的河槽部分。
a.河槽土质均匀时可按下式计算:

式中,hp为一般冲刷后的垂线水深,m;h为冲刷前垂线水深,m;P为冲刷系数。
b.河槽土质不均匀时可按下式计算:
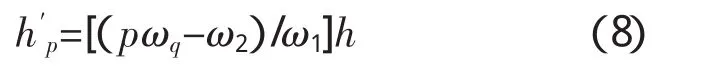
式中,h′p为河床中易冲刷部分冲刷后的水深,m;ωq为冲刷前桥下净过水面积,m2;ω1为冲刷前易冲刷部分的净过水面积,m2;ω2为冲刷后不可冲刷部分(表层土壤被冲去后)的净过水面积,m2。
1.2 局部冲刷深度计算方法
目前国内外采用最多的局部冲刷计算公式主要有65-1公式、65-2公式和包尔达可夫公式。
(1)65-1公式和65-2公式:
从20世纪50年代后期开始,我国铁路系统和公路系统对非粘性土河道桥墩局部冲刷进行了研究。根据我国有关局部冲刷的实测资料,在1964年的全国桥渡冲刷汇总工作会议上,制定了65-1公式和65-2公式[1]。两个公式已经过广泛应用与验证,精度较好,具有一定可靠性。
a.65-1公式:
当V≤V0时,hB=kξkη1b10.(6V-V0′)
当V≥V0时,
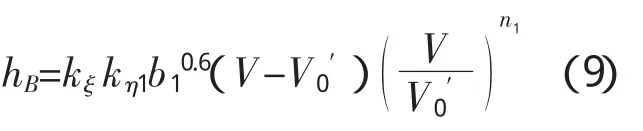
b.65-2公式:
当 V ≤V0时,
当V≥V0时,
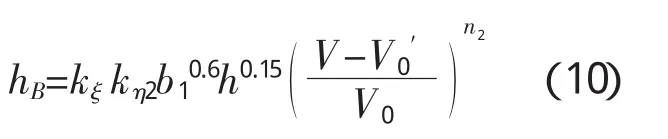
式中,hB为桥墩局部冲刷坑深度,m;kξ为墩形系数,可查有关表;b1为桥墩计算宽度,m;V为一般冲刷后垂线平均流速,m/s;h为一般冲刷后水深,m;V0为床沙起动流速,m/s;V0′为始冲流速,n1=1/([V/V0)0.2d0.15];n2=1/([V/V0)0.23+0.19lgd];d为床沙平均粒径,mm。
(2)包尔达可夫公式:
在国外的局部冲刷计算公式中,包尔达可夫公式结构相对简单,对大量野外实测资料等要求较少,因此得到了广泛应用。其公式形式为:
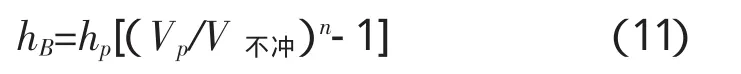
式中,hB为局部冲刷水深,m;hp为一般冲刷水深,m;Vp为设计流速,m/s;V不冲为不冲刷流速,m/s;n为墩台形状系数,一般取1/4~2/3[6]。V不冲和n均可以查相应图表得到。
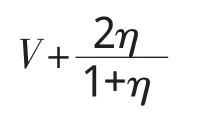
其中,Vp的计算应符合下列规定:式中:V为行进流速,m/s;η为水流流速分配不均匀系数。
(3)其他公式:
除了上述比较常用的公式外,还有基于现场实测资料、模型试验得来的经验公式,如Jain.c.c Lacey公式和Lacey公式。还有基于一定理论,通过建立一些假定来推出来的半经验半理论公式等。由于这类公式的参数需要根据具体情况而定,具有一定的不确定性,因此使用较少。
2 桥墩冲刷计算
2.1 桥梁现状
宾西铁路桥等5座桥,位于公阿什河下游哈尔滨市城区段约25 km,范围内有11座跨河公路桥梁和1座跨河铁路桥梁。长江路桥等级较高,属于城市主干道,但大都建设年代久远,桥下过水流速大,冲刷严重。因此本文选择长江路桥、绕城高速跨河桥、东方红桥、宾西铁路桥和伏尔加桥5座跨河桥梁进行冲刷计算,其平面位置见图1所示。桥梁基本情况为:长江路桥的桥梁规模属于大桥,公路等级为1级,桥孔有16孔,每孔净宽25 m,全长407 m,桥墩宽1.8 m,桥面底高程为124.06 m,河底高程为114.8 m,防洪标准为100 a一遇;绕城高速跨河桥的桥梁规模属于大桥,公路等级为1级,桥孔有13孔,全长390.4 m,桥面底高程为125.95 m,河底高程为118.33 m,防洪标准为100 a一遇;东方红桥的桥梁规模属于大桥,公路等级为2级,桥孔有8孔(14.5 m+15.8 m+15.8 m+15.8 m+15.8 m+15.8 m+15.8 m+14.3 m),桥墩宽1.0 m,桥面底高程为127.54 m,河底高程为120.1 m,防洪标准为100 a一遇;宾西铁路桥的桥梁规模属于中桥,等级为2级,桥孔有10孔,全长330.4 m,桥柱直径3.0 m,桥面底高程为129.56 m,河底高程为121.20 m,防洪标准为100 a一遇;伏尔加桥有 6 孔(19.98 m+20.0 m+19.98 m+19.98 m+20.0 m+19.98 m),桥墩宽1.0 m,桥面底高程为132.51 m,河底高程为125.1 m,防洪标准为100 a一遇。
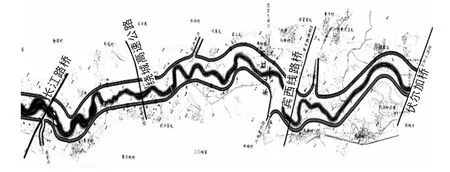
图1 阿什河城区段5座桥梁平面位置示意图
2.2 河道水文情况
阿什河位于哈尔滨市东部,是松花江右岸的一级支流。河道发源于尚志市帽儿山镇尖山砬子,于哈尔滨水泥厂附近注入松花江,干流总长213 km2,流域总面积3 518 km2[7]。流域大部分地形起伏坡降大,东南高、西北低。阿什河是半山区河流,上游为山区,地势较高坡降较大,水流湍急;中游为丘陵地区;下游为平原河流,河谷宽阔、地势低平,河漫滩与松花江河滩相连,该地区也是阿什河流域主要农业生产区。查《黑龙江省水文图集》流域多年平均悬移质输沙模数约为30(t/km2)/a,考虑输沙量有逐年加大的趋势,根据水文图集分析结论,修正后年输沙模数为45(t/km2)/a。由此计算流域多年平均悬移质输沙量为16.1万t/a。推移质按悬移质的30%估算。
阿什河干流道外香坊段防洪及河道整治工程,位于下游的香坊和道外两区境内,河段总长约25 km,地貌单元为阿什河河漫滩,沿线地势略有起伏,地形变化不大。工程上游从阿城区伏尔加桥开始,下游到阿什河入松花江河口为止,主要涉及香坊区成高子镇、幸福镇、向阳乡、道外区团结镇和阿城区程家店村。道外和香坊段区共4段堤防,总长15.92 km,排水闸3座,跨河公路桥11座和跨河铁路桥1座。由于上游地势高坡度大,河流泄洪能力低,容易形成洪水灾害,对桥梁、道路及水利工程造成破坏,再加上区间内跨河公路桥梁建设年代久远,部分桥梁冲刷损坏严重,影响正常使用,因此,本文针对工程范围内部分桥梁进行桥梁冲刷计算,为桥梁防护工程提供参考依据。
2.3 桥墩冲刷模式与参数选择
2.3.1 桥梁水文参数
通过实测资料和相关计算,可以得到5座桥梁的基本水文参数,见表1所列。
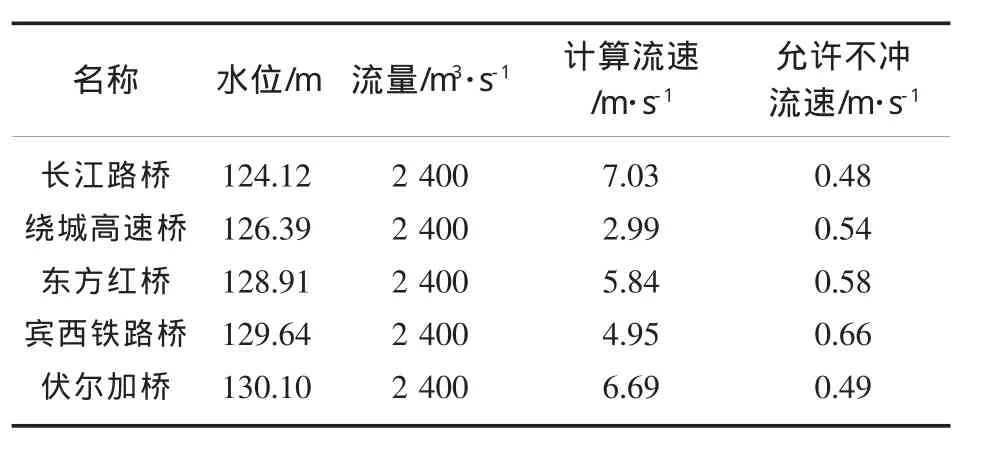
表1 阿什河城区段5桥梁水文参数表
2.3.2 一般冲刷计算
研究区段河道属于平原蜿蜒性河流,是稳定河段,本文选择了基于别列柳伯斯基假定建立的包尔达可夫公式,进行桥梁一般冲刷计算:
hp=Ph
公式中各参数意义见上文。其中冲刷系数P的最大允许值见表2所列。
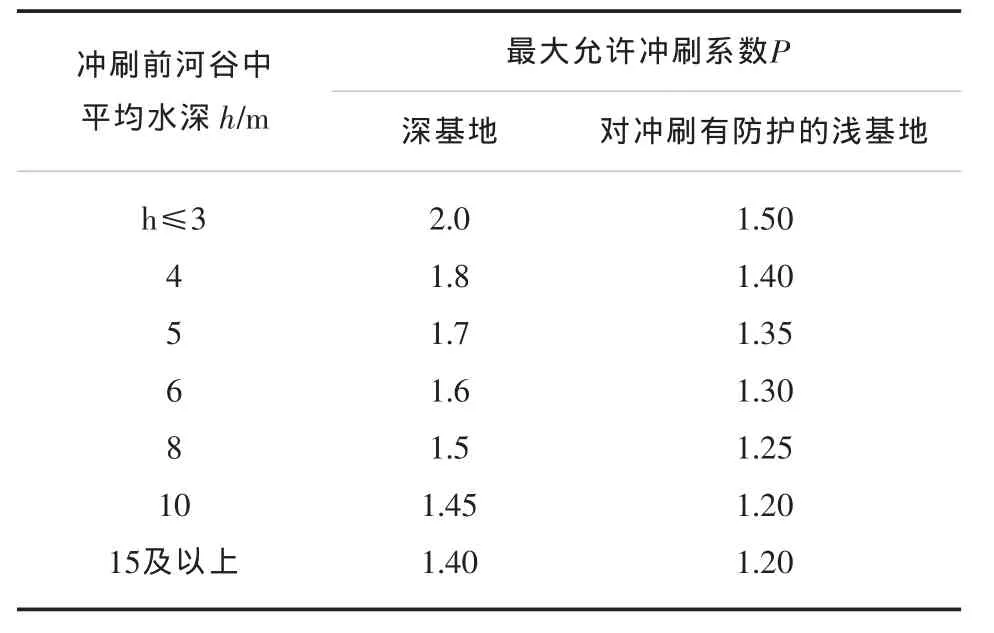
表2 P值最大允许值[6]一览表
由于研究区域位于阿什河下游段,地貌为河漫滩,属于宽浅型河道,且桥梁为进行过防护的浅基桥梁,故该项计算冲刷系数P选择1.4。
2.3.3 局部冲刷计算
无论是理论推导得出的理论公式,还是由实验推导的经验公式,都需要收集河道中大量野外实测水文、泥沙数据和模型实验数据,并且结构比较复杂。而包尔达可夫公式结构简单,使用方便,是迄今常用的国外方法。因此本文选择包尔达可夫局部冲刷公式来进行计算:
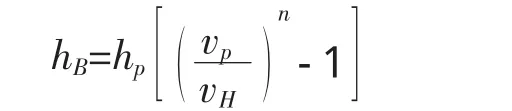
公式中参数意义见上文。其中,桥墩形状系数取0.5。
2.4 结果与分析
根据包尔达可夫公式,5座桥的一般冲刷结果、局部冲刷结果及局部冲刷与一般冲刷结果比值见表3所列。

表3 阿什河城区段5座桥梁冲刷计算结果一览表
根据资料可知[8],桥梁墩台及一些建筑物的局部冲刷与一般冲刷比值约为1.5~4。由计算结果可以看出,5座桥梁中4座的局部冲刷与一般冲刷比值结果均在1.5~4的范围内,绕城高速公路桥为1.07,接近1.5。可见,该5座桥梁冲刷计算结果是合理的。
3 结论与建议
(1)本文主要针对桥梁冲刷计算进行了浅析,分别介绍了国内外比较常用的一般冲刷计算方法和局部冲刷计算方法。针对阿什河哈尔滨城区段水文、水流、河道地貌、河床地质等特性,选择了基于别列柳伯斯基假定建立的一般冲刷公式、包尔达可夫公式,分别进行了河道上5座跨河桥梁的一般冲刷计算和局部冲刷计算。
(2)分析表明,在进行一般冲刷计算时,包尔达可夫公式对于平原蜿蜒形河流及山区稳定性河流都比较合适,并且该公式结构简单,对实测资料要求较简单,因此在实测资料比较难获取的河道或是工程前期规划中,更为实用。
(3)包尔达可夫公式显示,桥墩墩形系数对冲刷结果有影响作用,因此建议桥梁设计适宜选择对水流影响小的墩台形状,以此来优化墩形系数,从而减小墩台冲刷,保证桥梁自身的安全。
(4)计算表明,5座桥梁墩台都存在不同程度的冲刷,需要进行桥梁防护。可以沿桥梁下游方向,按1∶4河底冲刷坑坡度计算,作为防护长度。防护措施可采用抛石防护、混凝土模袋防护或混凝土铰链排防护。
(5)同时,长江路桥和伏尔加桥对河道断面缩窄过大,上下游形成较大水位差,过水流速较大,冲刷较为严重,建议采取桥梁扩孔措施,减小桥梁阻洪,以此减小桥墩冲刷。
[1] 董年虎,段文忠.国内外非粘性土桥墩局部冲刷计算方法综述[J].郑州工业大学学报,1997,(18):94-99.
[2] 高冬光.桥梁一般冲刷64-2公式的简化形式[J].西安公路学院学报,1984,(2):30-38.
[3] 卜海磊,杨娜,张罗号.黄河下游桥渡冲刷计算问题探讨[J].人民黄河,1997,(31):30-38.
[4] TB10017-99,铁路工程水文勘测设计规范[S].
[5] 阚泽.桥渡冲刷[M].北京:中国铁道出版社,2004.
[6] 李炜.水力计算手册(第二版)[M].北京:中国水利水电出版社,2006.
[7] 管立志,孙旭.浅谈阿什河流域整治工程中应注意的问题[J].水利科技与经济,2012,(18):47-48.
[8] 吴雪茹.桥墩一般冲刷计算研究[J].水运工程,2007,(5):27-30.
