斜靠式系杆拱桥静力特性及稳定性分析
2014-01-08王艳军孙书亭
王艳军,孙书亭
(中国市政工程华北设计研究总院,天津市 300074)
0 引言
斜靠式系杆拱桥一般由4片拱肋组成,中间2片主拱为平行拱肋,主拱外侧各设一片倾斜辅拱[1]。斜靠式系杆拱桥属于无推力的拱、梁组合结构,主、辅拱通过端横梁和风撑连接在一起,整个结构可以看作是简支在桥墩上的外部静定结构。由于车行道两侧的主拱之间无横向联系,相比一般的系杆拱桥,斜靠式系杆拱桥桥面上视野开阔,行车无局促压抑感,并且因其造型美观,所以在城市景观桥设计的桥型选择中具有明显的优势。
1 工程简介
某桥主桥结构形式为斜靠式系杆拱桥。主拱、辅拱的拱轴线均采用二次抛物线,其中主拱拱肋矢跨比1∶5,矢高19.84 m,计算跨径99.2 m,辅拱向主拱侧倾斜24°,矢跨比为1∶4.7,矢高21.10 m,计算跨径99.2 m。主拱、辅拱拱肋及主拱系梁截面形式均为矩形带肋钢箱,截面尺寸:主拱为1.4 m×1.8 m,辅拱为1.2 m×1.4 m,端横梁为2.0 m×2.0 m。主拱系梁为刚性系梁,截面尺寸为1.4 m×2.5 m,辅拱设预应力钢绞线柔性水平系杆。每侧主拱、辅拱通过端横梁和7道风撑连接在一起。风撑间距12 m。主拱、辅拱拱肋及主拱系梁均采用Q345qD钢材。桥面系为钢-混凝土组合梁,桥面板采用25 cm厚C40钢纤维混凝土现浇板。吊杆采用PES(FD)7—37和PES(FD)7—109高强镀锌平行钢丝束防腐吊索,吊杆间距4.0 m,主拱、辅拱各有44根、48根吊杆。
由于斜靠式系杆拱桥空间效应明显,结构受力复杂,稳定性问题突出,所以本文以该工程为背景,利用有限元软件对其静力特性和稳定性进行了分析研究。为同类桥型的设计提供参考。
2 结构静力特性分析
2.1 有限元模型的建立
采用桥梁专用计算软件Midas Civil建立有限元模型:采用空间梁单元模拟主、辅拱拱肋、主拱系梁、横梁、纵梁、风撑,用桁架单元模拟主、辅拱吊杆和系杆,支座采用弹性连接输入支座刚度来模拟。针对桥面系为钢-混凝土组合梁,在模型中采用了施工阶段联合截面来处理后浇混凝土与钢梁的叠合情况。模型中节点945个,梁单元1 167个,桁架单元138个,弹性连接8个,刚性连接116个。有限元整体计算模型如图1所示。

图1 有限元模型
2.2 拱肋、系梁应力计算
有限元模型在整体静力计算中根据桥梁的施工步骤分成了8个施工阶段。计算时考虑了结构自重、二期荷载、整体升降温、温度梯度效应和城A—级汽车荷载、人群荷载及风荷载外,还考虑了钢-混凝土组合梁混凝土的收缩及徐变效应。
成桥阶段主、辅拱拱肋、主拱系梁及端横梁在荷载组合为恒载+可变荷载(最不利组合)下,各项应力最大值见表1。
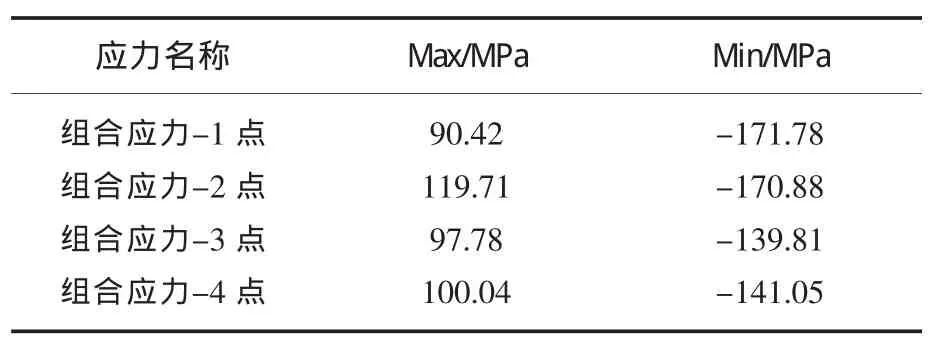
表1 应力结果表格
从计算结果中可以看出结构最大压应力171.78 MPa,出现在主拱拱脚处,最大拉应力119.71 MPa,出现在主拱系梁拱脚处。应力均小于Q345qD钢材的应力允许值,因此结构应力满足设计要求,桥梁结构受力合理可靠。各项应力结果如图2~图5所示。
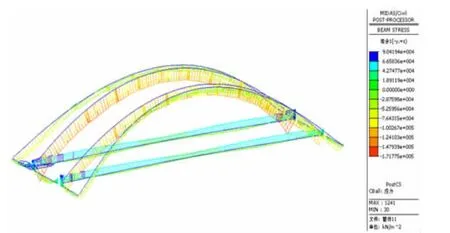
图2 组合应力-1点
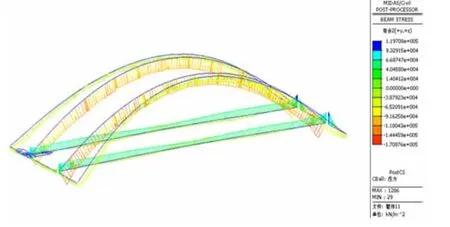
图3 组合应力-2点
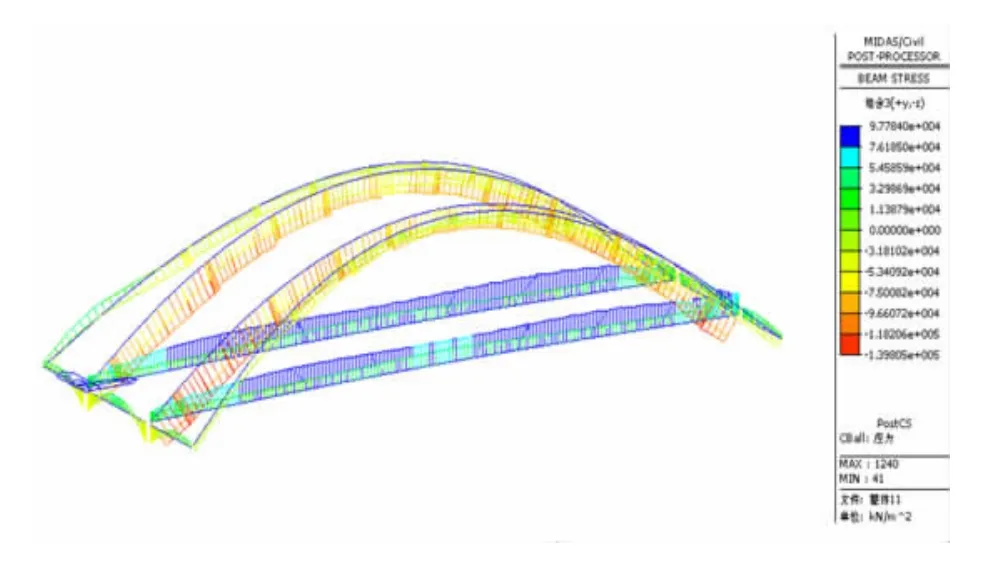
图4 组合应力-3点
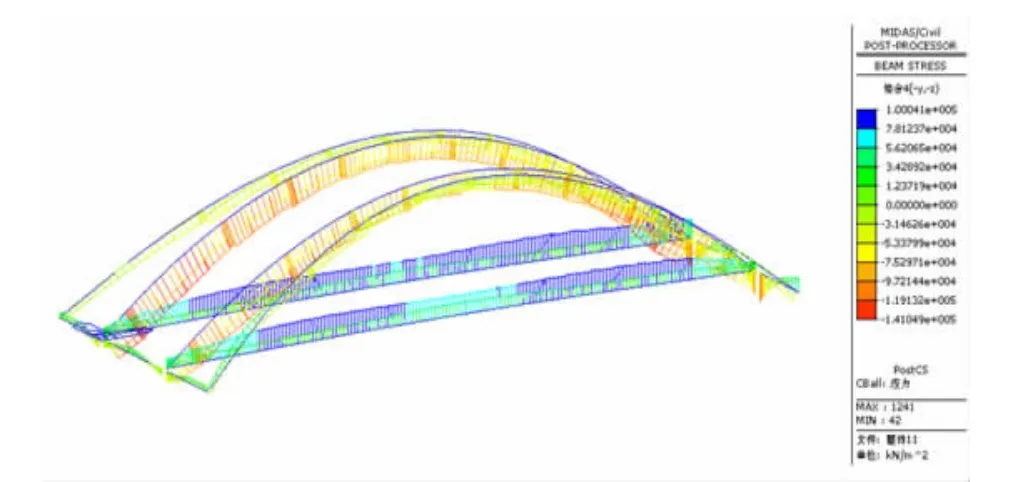
图5 组合应力-4点
2.3 吊杆应力计算
成桥阶段,在恒载+可变荷载(最不利组合)下,主拱吊杆最大应力为624.5 MPa,安全系数2.67;辅拱吊杆最大应力为326.2 MPa,安全系数5.1,满足拱桥设计要求吊杆最小安全系数不得小于2.5的规定。吊杆应力都小于吊杆的容许应力[σ]=0.4Rb=668 MPa。主、辅拱吊杆应力幅见图6、图7(吊杆按小桩号至大桩号顺序编号)。计算结果表明主、辅拱吊杆最大应力幅分别为115.7 MPa和109.26 MPa,均满足应力幅度不超过200 MPa的设计要求。
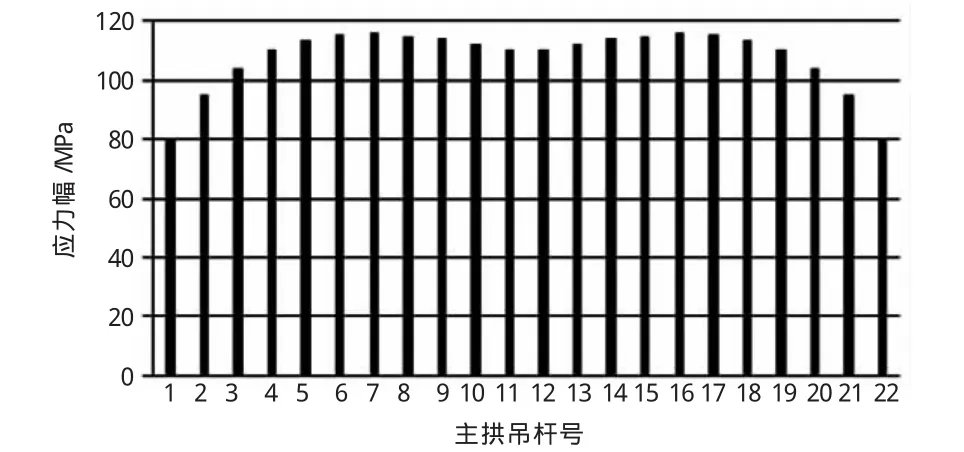
图6 主拱吊杆应力幅
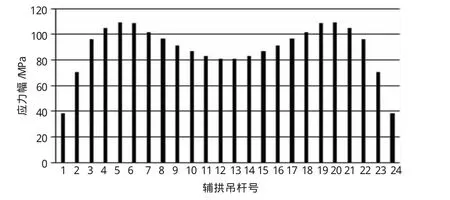
图7 辅拱吊杆应力幅
3 稳定性分析[2,3]
3.1 稳定性分析的理论和方法
斜靠式系杆拱桥的拱肋是以受压为主的结构构件,稳定问题是拱桥设计中不可忽略的问题。
结构失稳是指在外力作用下结构的平衡状态开始丧失稳定性,稍有扰动则变形迅速增大,最后导致结构遭到破坏。
结构失稳有两种性质根本不同的失稳形式。
第一类稳定:分支点失稳,是以小位移理论为基础的线弹性最小特征值屈曲问题,用于确定一个理想弹性结构的理论屈曲强度。第二类稳定:极值点失稳,是建立在大位移非线性理论的基础上,即考虑了结构几何非线性和材料非线性情况下的极限承载力问题。
实际工程中的稳定问题都属于第二类稳定问题,但是,因为第一类稳定问题的力学情况比较单纯,在数学上作为求本征值也比较容易处理,而它的临界荷载又近似地代表相应的第二类稳定的上限,所以在理论分析中第一类稳定问题更有研究价值。工程中通常以第一类稳定问题的计算结果作为设计的依据。
第一类稳定问题通常采用数值解法,有限元方法是目前最常用的,即首先将结构离散成为有限个单元,然后通过特征方程求得结构的弹性临界荷载:
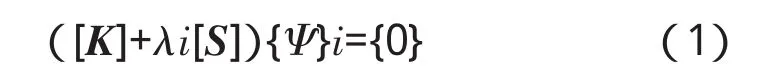
式(1)中:[K]为刚度矩阵;[S]为应力刚度矩阵;λi为第i阶特征值,即第i阶屈曲荷载系数;{ψ}i为对应特征值λi的特征向量,即屈曲模态。
式(1)就是弹性屈曲问题的控制方程,求解方程可以得到特征值λi,即结构的第一类稳定系数。
3.2 稳定性分析结果
一般来说,结构的稳定系数对应于施加于结构上的某种特定的作用或作用效应组合。该桥在结构第一类稳定性分析中采用了以下3种组合。
(1)组合一:恒载
(2)组合二:恒载+风+偏载(汽车、人群)
(3)组合三:恒载+风+满载(汽车、人群)
各作用组合下结构前三阶稳定系数及失稳特征见表2,第1阶失稳模态见图8~图10。
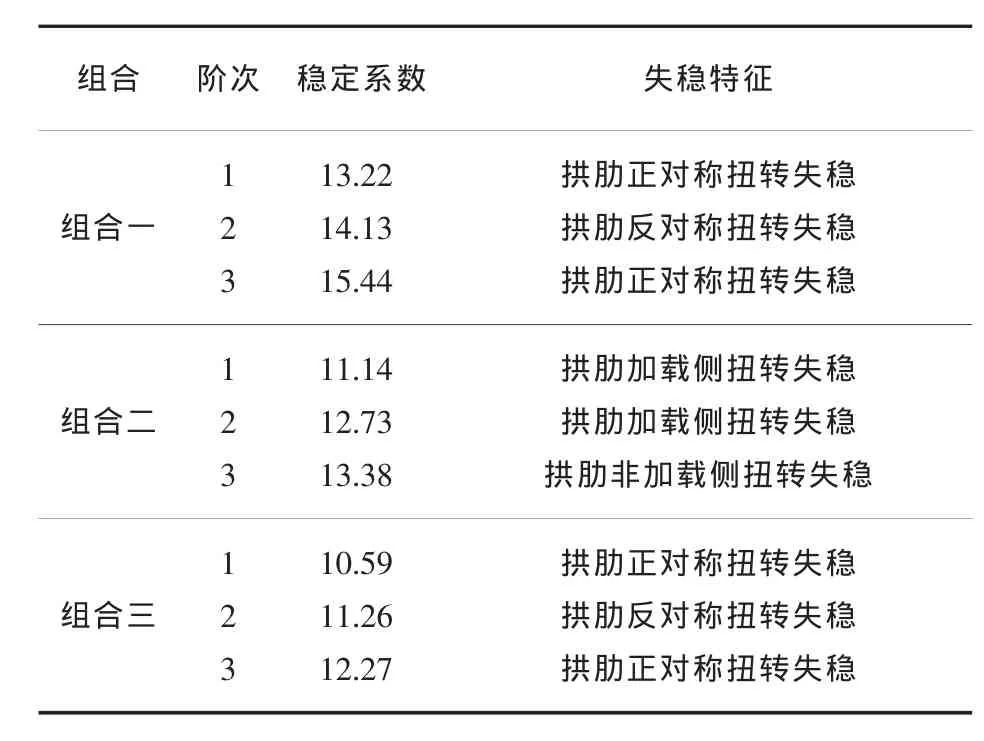
表2 稳定系数及失稳特征
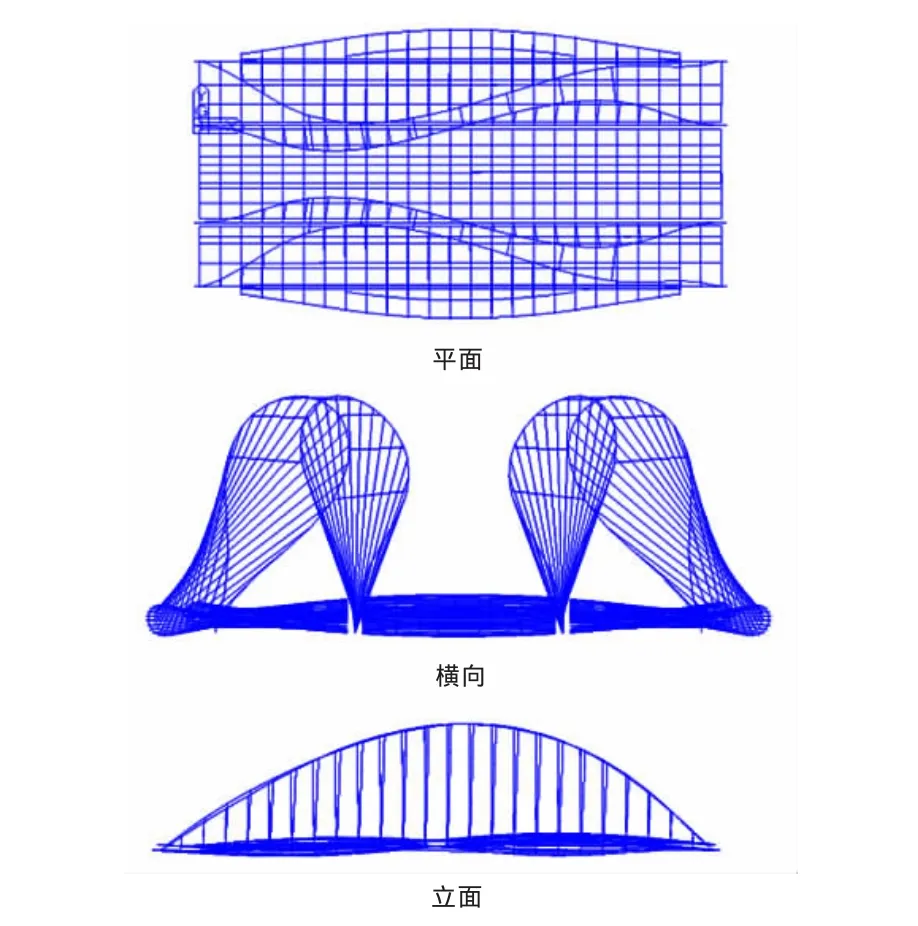
图8 组合一第1阶失稳模态:拱肋正对称扭转失稳
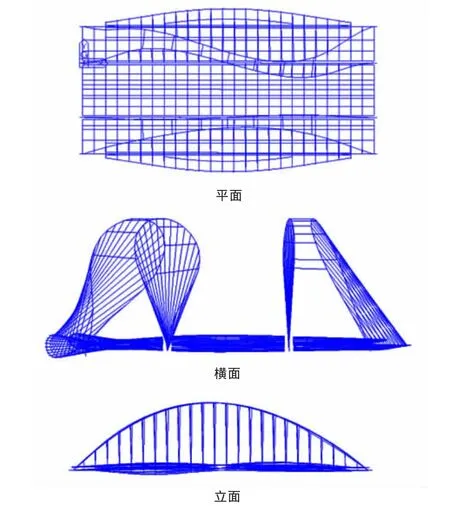
图9 组合二第 1阶失稳模态:拱肋加载侧扭转失稳
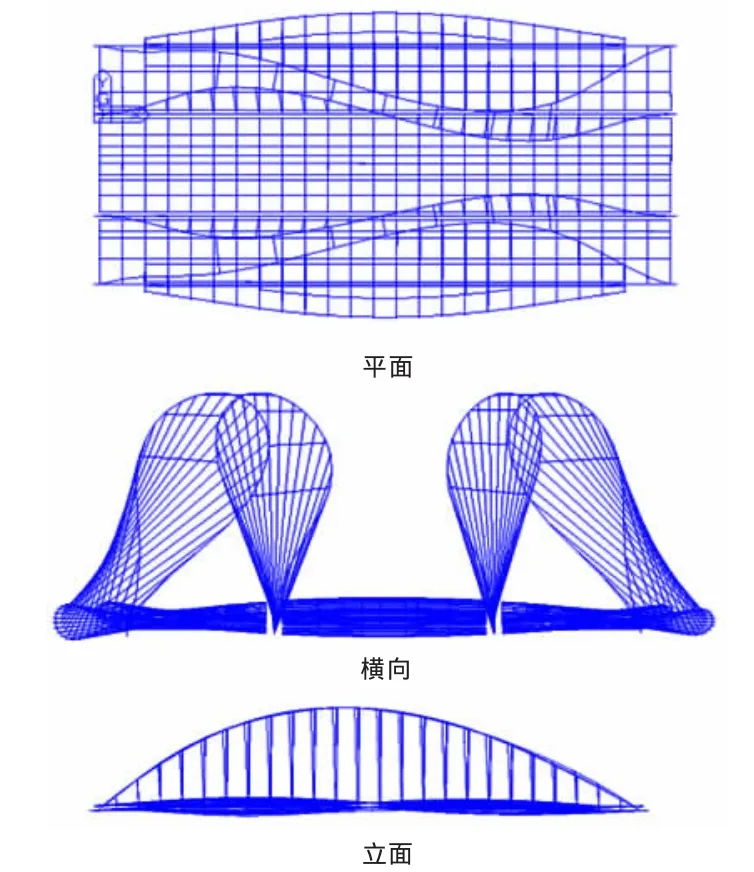
图10 组合三第1阶失稳模态:拱肋正对称扭转失稳
从以上计算结果可知,在各作用组合下,结构第1阶稳定系数为10.59~13.22,满足关于一般拱桥稳定系数大于4~5的规定。失稳模态均为拱肋面外扭转失稳。第1阶失稳模态为扭转失稳是因为主、辅拱拱顶风撑处的横向刚度相对较大,又由于主、辅拱拱脚均固结于横梁,刚度也较大,所以拱肋上横向刚度较小的无风撑区域在外荷载作用下先发生较大变形导致拱肋出现扭转失稳。
风撑的设置不仅对提高结构的稳定性起到非常大的作用,并且改变了结构的失稳特征。以组合三为例,不设置风撑时结构稳定系数为4.53,比设置风撑时的稳定系数降低约57.2%。因为主、辅拱拱肋之间无风撑联系而相互独立,横向刚度大大降低,所以不设置风撑时,结构第1阶矢稳模态为拱肋横向侧倾失稳,如图11所示。
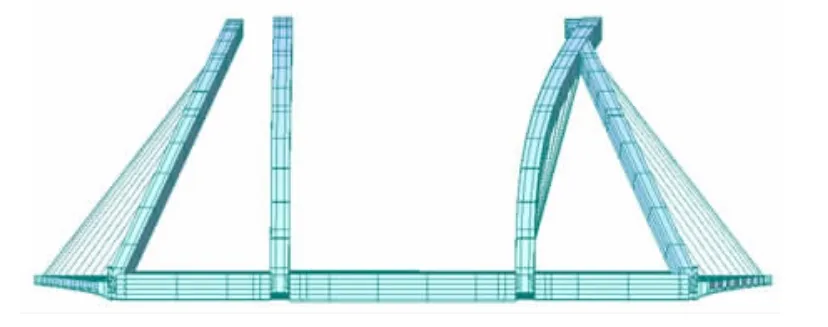
图11 无风撑第1阶失稳模态
结构的纵向失稳以第一种工况为例,直到第6阶才出现,如图12所示。说明这种斜靠式系杆拱桥的纵向刚度要远大于横向刚度。
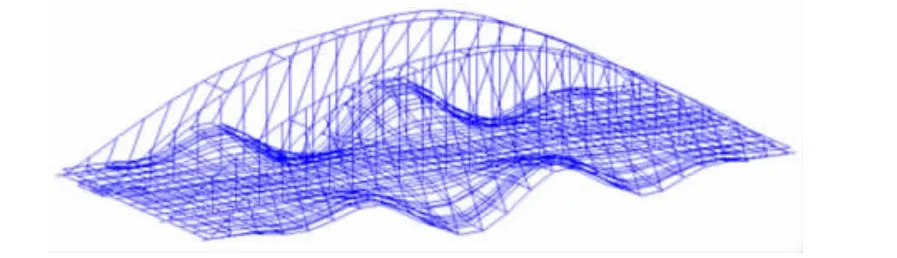
图12 纵向失稳
4 结论
本文以某斜靠式系杆拱桥为背景,采用有限元模型分析研究了结构的静力特性和稳定性,得出以下结论:
(1)在荷载最不利组合下,主、辅拱拱肋、系梁、吊杆应力和吊应力幅均满足设计要求,桥梁结构受力合理可靠;
(2)不同作用组合下结构第1阶稳定系数为10.59~13.22,满足关于一般拱桥稳定系数大于4~5的规定;
(3)结构失稳模态均为拱肋的面外扭转失稳;
(4)风撑的设置不仅提高了结构的稳定性,还改变了结构的失稳特征。
[1]肖汝诚,孙海涛,贾丽君,等.斜靠式拱桥[J].上海公路,2004(4):22-26.
[2]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,1992.
[3]陈宝春.钢管混凝土拱桥(第二版)[M].北京:人民交通出版社,2007.
