一种沥青路面车辙形成的分析方法及工程应用
2014-01-08周福婷范厚彬
周福婷,范厚彬
(1.浙江浙西高速公路管理有限公司 ,浙江杭州 310013;2.浙江舟山跨海大桥有限公司,浙江舟山 315040)
1 问题的提出
随着我国交通事业的发展,对路面结构使用性能的要求越来越高。车辙是沥青路面的主要病害之一,它影响路面的平整度,降低路面的使用品质,如果车辙累积过快,则直接影响路面的使用寿命。我国近几年来,交通量及交通荷载不断增加,交通管理的改善使车辆行驶渠化,这些因素都促使沥青路面在较短的使用年限内产生过大的车辙量。因此,对车辙的研究便显得日趋必要,同时,它也成为目前道路工程的热点和难点之一。国内外的许多研究者在这方面做了大量的研究。一般认为,沥青路面的车辙主要由三部分组成:一是沥青混合料在荷载作用下进一步压密引起的车辙,此为沥青路面通车初期所形成的车辙大部分是因进一步压密形成的;二是在交通荷载作用下,沥青混合料发生剪切形变而形成的车辙,这种剪切变形在高温季节进一步加剧;三是由于沥青路面结构层在荷载作用下产生损坏而形成的车辙。大量研究表明,沥青混合料是一种典型的粘弹塑性材料,它会随时间、温度和承受的应力而发生形变,在低温条件下呈弹性,在高温条件下呈粘性特点,表现为在高温和长时间荷载作用下,会产生粘性流动,路面即出现车辙病害。
综上所述,把沥青混合料视为粘弹性塑性本构关系,符合沥青路面车辙形成这种现象。笔者在拟把沥青混合料视为具有强大包含性的层叠流变本构模型,进行车辙形成机理的数值模拟研究。
2 描述沥青混合料本构关系的层叠流变模型基本原理
“流变”(reeology)一词来源于古希腊哲学家Heractitus所说的“ ”,意即万物皆流。原则上讲,所有实际物体都具有流变特性。山,经历长久的地质年代可发生流动,只是时间太长,不为普通人所注意。1922年Bingham《流动和塑性》名著的出版,以及根据他的倡议,1928年流变协会的成立,标志着流变学成为一门独立的学科。如今流变学正广泛应用于建筑材料等许多方面。它的基本课题是研究应力-应变状态的规律及其随时间的变化,并根据所建立的本构规律去解决工程实际中遇到的与流变有关的问题。为学者们从微观和宏观两方面对建筑材料的流变性质进行研究。前者着重从建筑材料的微观结构研究其具有流变性质的原因和影响建筑材料流变性质的因素,它只能做定性分析。后者则假定建筑材料是均一体,采用直观的物理流变模型来模拟建筑材料的结构,通过数学力学分析,建立相关的公式,定量分析建筑材料的流变性质及其对工程的影响。各国学者所做的大部分工作属于宏观流变学的范畴。
文献[1]提出的图1所示的2N+1参数层叠模型,它含有弹性、粘弹性、粘塑性元件,它是一个比较完整的模型,能描述一般建筑材料流变性态。该模型具有2N+1个元件,相应有2N+1个参数,而试验数据只有时间位移曲线,并且位移与时间之间关系是非线性关系,用数学方程表达出这一关系来应是一个非线性方程。层叠流变模型具有强大的包含性,即通过参数控制,它可包含常见的各种建筑材料流变本构模型,也就是说,通过对它选取不同参数值的方法就可形成许多不同的流变模型。层叠模型具有概念简洁、组合规律性强、易于在计算机上实现的优点。这一研究成果为解决以下问题提供了新的思路:(1)可把流变本构模型的识别转化为参数识别,实际上可使模型识别与参数识别同时实现,从而可克服建筑材料本构模型辩识过程中强烈依赖于特定模型的不足;(2)可避免工程计算在本构模型选择中的主观性;(3)对于数学公式复杂、模型构造及其参数无规律的流变模型可通过参数转化到层叠模型身上而较容易得到工程应用。笔者认为,该层叠流变本构模型还应具有如下特点:
第一、具有包含性,可以适应各种不同建筑材料本构模型的要求;
第二、在能反映建筑材料流变规律的前提下,可寻找到较最简单的模型;
第三、易于在计算机上实施。
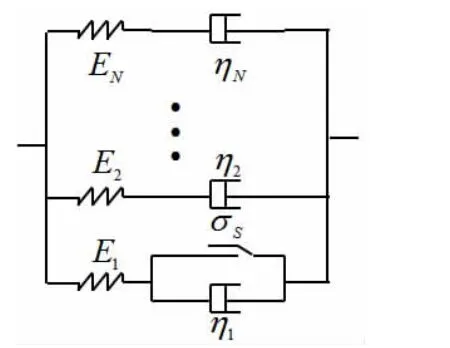
图1 2N+1层叠模型
笔者认为,沥青混合料作为一种复合材料,是典型的弹、粘、塑性综合体,在低温小变形范围内接近线弹性体,在高温大变形活动范围内表现为粘塑性体,而在通常温度的过渡范围内则为一般粘弹性体。在行车荷载作用下,沥青混合料的特性十分复杂,实际工作范围内主要表现为非弹性体,变形在卸载后具有不可恢复性。层叠模型包括了弹性、粘性、塑性元件,能较好地反映沥青混合料行为特征。因此,从这个角度,采用层叠模型来描述沥青混合料的流变力学特性是合适的。为方便,图1中N值取2,层叠模型演化为图2的五参数层叠模型。它作为本文沥青混合料的本构关系。

图2 五参数层叠模型
3 沥青混合料的层叠模型有限元编程原理
3.1 单元刚度矩阵形成原理
层叠模型由N层Bingham流变模型并联组成,在受力时每个叠层具有相同的变形。层叠模型的单元刚度矩阵为:

式中:ti——各叠层的加权系数,它一般需满足,ti可为负值,赋以负值时可以模拟材料的应变软化;
[Bn]——应变矩阵;
D^j——粘弹塑性应力增量计算中的等效物理矩阵,由于每一叠层的材料特性各异,故各个叠层的矩阵D^nj也各不相同;
N——模型叠层总数。
3.2 层叠模型有限元计算步骤
层叠模型求解过程的主要步骤整理如下:
(1)假定在 t=ti时刻有一平衡状态,且 dn、εn、Fjn、σn、σjn值已知,j=1到 N,N 为材料层叠数,σjn为材料各叠层所受应力,σn为总应力,可得到以下量值:
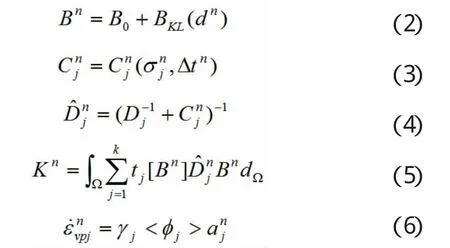
(2)加入权系数计算位移增量Δdn:
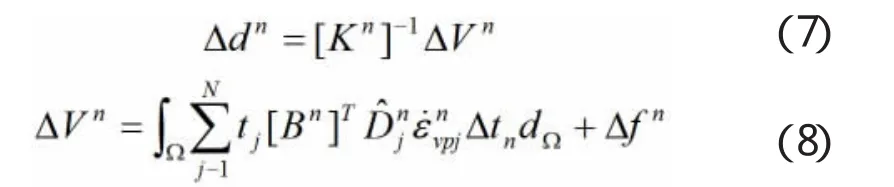
按下式计算应力增量 Δσjn、Δσn:

(3)求总位移、总应力和各层应力:
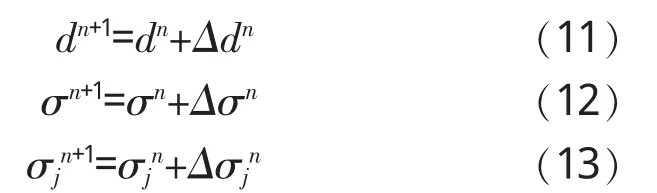
(4)计算粘塑性应变率:

(5)进行平衡的修正。首先利用位移dn+1来计算Bn+1,将应力σn+1代入平衡方程中,并计算如下的残应力φn+1:
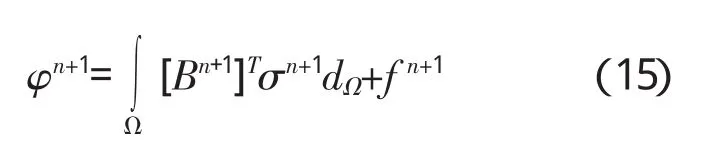
将上面各式加到伪荷载增量矢量,以便为下一时间步长计算之用:
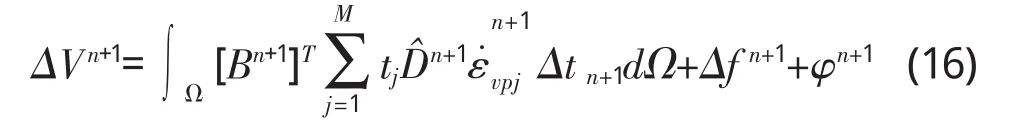
4 程序编制及实例演算
根据上述沥青混合料的层叠模型有限元编程原理,采用Visual Fortran编制了相应的计算软件V2D_229C,其界面见图3所示。由于该计算软件V2D_229C前、后处理功能差,笔者编制了相应的单元网格剖分软件draw,其界面见图4所示。

图3 计算软件V2D_229C界面图示
图4 单元网格剖分软件draw界面图示
根据浙江省某长山坡路面工程特点,结合其它路面工程,采用以下标准断面几何尺寸的路面体系进行数值模拟研究实例。其路面结构为:表面层为4 cm细粒式沥青混凝土(AC-13型),中面层为6 cm中粒式沥青混凝土(AC-20型),下面层为8 cm粗粒式沥青混凝土(AC-25型),上基层为18 cm厂拌二灰稳定碎石,下基层为18 cm厂拌二灰稳定碎石,底基层为18 cm厂拌二灰稳定碎石,路面总厚度为72 cm。路基厚度取500 cm。沥青混合料面层的本构模型为图2的5参数层叠模型,厂拌二灰稳定碎石、路基的本构关系为线性弹性材料。该项模拟研究主要考虑车辙深度,因此,取一个矩形横断面看成平面应变进行计算是可以的,横向宽度取800 cm。计算时采用的位移边界条件为:模型底部边界在垂直和水平方向均固定,左右两侧的边界均为垂直方向为自由,而水平方向为固定。轮压取p=730 kPa。采用多荷载步来模拟运动的荷载,每个轮载持续作用的时间为0.1 s。
采用自制软件Draw进行网格剖分,单元总数为638个,节点总数为2 017个。有限元网格图见图5所示。
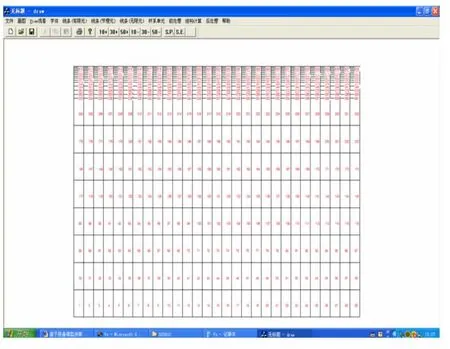
图5 有限元网格图
通过5 000次循环荷载的计算,把各节点塑性变形整理成如下变形图(见图6)。最终收敛的车辙深度为2.19 mm。比一般车辙深度的实测结果要偏大,笔者认为,造成这个现象的原因主要是:沥青混合料随着温度的变化本构关系在变化,在低温下,表现成粘弹性,而在高温条件下表现为粘弹粘塑性,而本文采用的本构关系为5参数层叠模型,它本身就是一个粘弹粘塑性本构关系。从这点似可以进一步得到结论:车辙主要是高温下沥青混合料表现出了粘塑性性质而产生的永久变形。
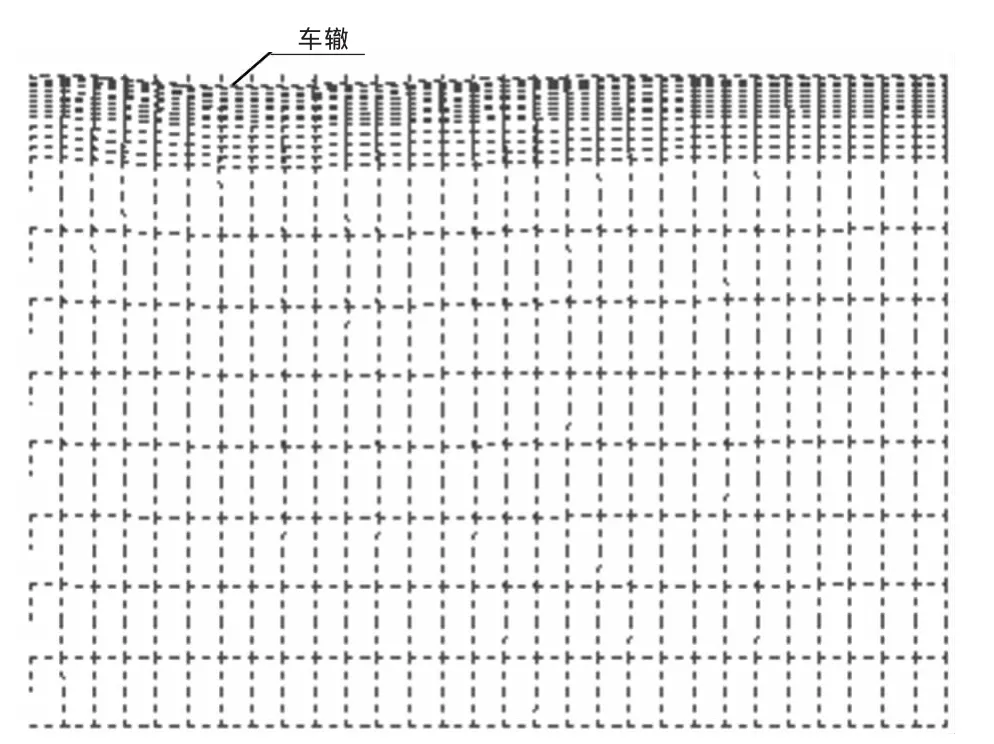
图6 5 000次循环荷载作用下塑性变形图
5 结语
通过本文的研究,似可以得到以下结论:
(1)采用具有强大包含性的层叠模型来模拟沥青混合料粘弹粘塑性是合适的,可以解释车辙形成机理,可以体现沥青混合料的非线性、塑性、粘弹性、非线性粘弹性对沥青路面车辙的影响,较为全面地反映沥青路面永久变形的特性。
(2)要减少车辙深度,须改善沥青混合料温度稳定性能,特别是改善高温下呈粘塑性特点,如果高温下也呈粘弹性性质,便没有车辙形成的土壤。进一步研究沥青混合料的配合比是改善车辙形成的一大研究方向。
[1]范厚彬.基于层叠模型的盾构隧道施工对周围环境的影响[D].上海:同济大学地下建筑与工程系,2003.
[2]冯紫良,范厚彬.软土流变试验的数值模拟[J].同济大学学报,2003,31(4):379-382.
[3]范厚彬,樊志化,陆耀忠.基于层叠模型的岩土材料流变本构关系识别[J].岩石力学与工程学报,2005,24(5):768-773.
[4]徐世法,朱照宏.按粘弹性理论预估沥青路面车辙[J].同济大学学报,18(3):299-304.
