对比电势能分析火积耗散计算

2014-01-07张明智李婷婷甄鹏洋

科技视界 2014年32期

张明智李婷婷甄鹏洋

（华北电力大学能源与动力工程学院，河北保定071003）

0 引言

过增元等[1]提出热量传递势容和热量传递势容耗散函数。通过对热量传递与电荷传递现象比拟，得出一个新的物理量火积—与电势能相对应，代表物体向外传递热量的能力。热量传递过程中传递能力的损失称为火积耗散。韩光泽等[2]将导热系统与导电系统类比，发现它们的传递能力的损耗都可以由广义功来反映。在力学系统中，功为强度量力与广延量力所走过的位移量的乘积。对于导电系统，广义功电功是强度量电势与广延量电荷的乘积；对于导热系统，广义功热力功是强度量温度与广延量热量的乘积。本文将涉及到的物理量进行了比拟，如表1所示：

表1 导电与导热系统相关物理量对照Tab.1 Contrast of related physical quantities of electrical and thermal conductive systems

目前关于火积的研究涉及到：火积的概念，火积传递效率[3]，火积耗散率，火积耗散极值原理[4]，火积耗散热阻[5]及其在传热传质优化中的应用[6]等。本文讨论了不同情况下火积耗散数学表达式，进一步明确火积耗散的物理意义和计算方法。

1 导电系统电势能耗散

1.1 电功与电势能

广义功电功，是强度量电势与广延量电荷的乘积，可以表示为微分式：

设带电量为Q的电容器，电势是φ，本构方程是Q=ceφ，将其对外放电，当电势由φ2达到φ1时，电容器对外做电功为：

电容器对外界做的电功等于一个状态函数的变化，在电磁学中，这个状态函数被定义为导体的电势能：

导体电势能的大小表征导体向外传递电荷的能力，电势能耗散量为导体向外做电功的大小。

1.2 电势能耗散计算

1.2.1 无源有限系统

设两个结构完全相同的电容器，电势分别为φ1、φ2，将其并联成为一个无内电源的有限体系。利用式（3）分别计算出并联前后的总电势能，两者的差就是电势能耗散。并联之前两电容器总电势能为：

并联后总电容是 2Ce，电势是（φ1+φ2）2，总电势能为：

并联过程中电势能耗散：

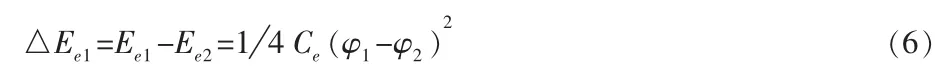
1.2.2 稳流开口系统

设将电荷量恒为Q的正电荷放在恒定匀强电场中，将其从φ1点移动到φ2点。当电荷沿等势线运动时，φ1=φ2，过程中没有电势能损耗。当电荷沿着电场线正向运动时，φ1＞φ2，过程中必有电势能损耗。从这两种不同移动电荷过程的比较分析中可以看出，产生电势能损耗的原因是存在电势差，高电势点输出的电势能大于低电势点得到的电势能。

基于对电势能损耗机理的认识可将电势能耗散定义为：

对于电量稳定的开口系统，由式（7）可知过程中的电势能耗散为：

1.2.3 一般系统

电势能损耗的定义式（7）反应了电势能损耗的机理，可以由此积分得到系统总的电势能损耗，但该式与时间无关，只能用于描述过程的结果。在研究某些具体问题时往往需要知道单位时间单位体积导电介质中的电势能损耗。将式（7）两端同时对时间和体积微分得：

式中：▽φ为电势梯度；J为电流密度，A m2。又已知存在下式：

式中：ψEe为电势能耗散率，J （s·m3）。

式（11）两侧同时对时间和体积进行积分得电势能耗散为：

2 导热系统与火积耗散

2.1 热力功与火积

定义温度T与被传输热量Qh的乘积为热力功Wh[7]，热力功可以表示为微分式：

设有一个质量和体积不变的物体放在热源上，热源缓慢的升高温度给物体加热。被加热物体的本构方程是Qh=ChT。其中Ch是热容，Qh是热容量。当物体的温度由T1升高到T2时，热源对物体做的热力功为：

热源对物体做的热力功等于一个状态函数的变化，这个状态函数被定义为火积：

火积是表征物体向外传递热量能力的物理量，火积耗散量为物体向外做热力功的大小。

2.2 火积耗散计算

2.2.1 无源有限系统

设有两个完全相同的物体，通过直接热接触后构成一个复合热系统。这是一个无源有限系统，利用定义式（15），分别计算出物体被加热前后的火积，两者的差就是火积耗散。

设接触前两个物体的温度分别是T1和T2，接触前两个物体的总火积为：

接触后复合系统的热容是2Ch，平衡温度是，接触后的总火积是：

组合过程中火积耗散为：

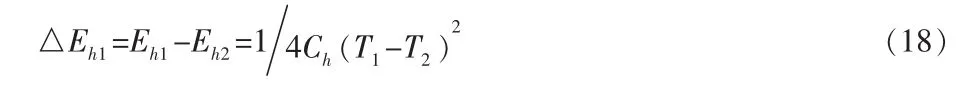
2.2.2 稳流开口系统

设一个质量和体积不变的物体放在热源上加热，物体其它各方面绝热。物体的温度为T，热容量为QV，热源的温度为T′。

文献[7]指出，当物体与热源之间无热阻的接触，T′=T，则该系统加热过程中没有火积耗散。当物体与热源之间有热阻，T′＞T，过程中必有火积耗散，并对火积耗散(文献中称为势容耗散)定义为:

该定义式的实质是热源的传热温度T′与系统内部温度T的差值所做的热力功，即热源所付出的火积多于被加热物体所能得到的火积。

以一维稳态导热为例，输入厚度为d的平板与输出平板的热流密度相等且都为q，由式（19）可得过程中的火积耗散为:

2.2.3 一般系统

火积耗散的微分定义式（19）反应了火积耗散的机理，可以由此积分得到系统总的火积耗散，但该式与时间无关，只能用于描述过程的结果。在研究某些具体问题时往往需要知道火积耗散率，也就是单位时间单位体积导热介质中的火积耗散。将式（19）两端同时除以时间和导热体体积的微分得:

又已知存在下式：

将式（22）代入式（21）得：

式中：ψEh为火积耗散率，。

式（23）两侧同时对时间和体积进行积分得火积耗散为：

3 结论

从上面的分析计算中可以看出，导电系统中的电势能损耗与导热系统中的火积耗散的机理是类似的。电势能损耗的机理是导电过程存在电势差，高电势点输出的电势能多于低电势点得到的电势能。火积损耗的机理是导热过程中存在温差，热源输出的火积大于被加热物体得到的火积。此外，二者在无源有限系统、稳流开口系统以及一般系统的表达式是一一对应的，不仅在形式上完全相同，而且在物理含义上也完全对应。这进一步说明，本文对火积耗散的数学表达式分析是正确的。关于火积耗散表达式的分析有助于在不同场合灵活采用不同的计算方法对火积耗散进行计算。