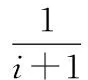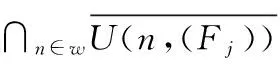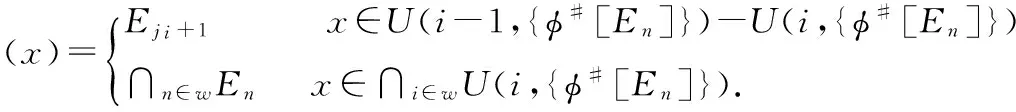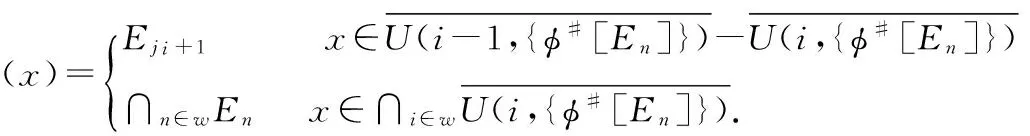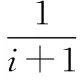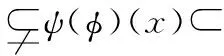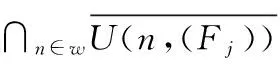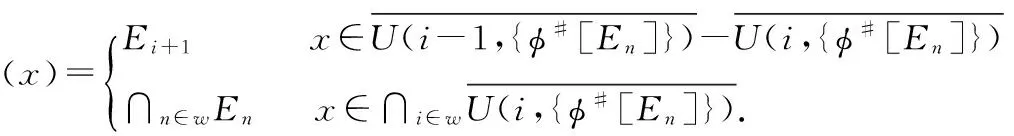Set-valued mappings and spaces havingsemi-stratifiable structure
2014-01-06-,-
-, -
(School of Mathematics and Computational Science,Wuyi University,Jiangmen 529020,China)
Set-valuedmappingsandspaceshavingsemi-stratifiablestructure
XIELi-hong,YANPeng-fei
(School of Mathematics and Computational Science,Wuyi University,Jiangmen 529020,China)
In this paper,we give some characterizations of stratifiable and semistratifiable spaces by the insertion of semi-continuous set-valued mappings.Also,we introduce the K-lower and K-upper set-valued mappings and,using them,give some characterizations ofk-semi-stratifiable spaces andk-MCM(kβ)spaces.
K-upper(K-lower)set-valued mappings;stratifiable space;semi-stratifiable space;MCM;MCP;k-MCM(kβ);k-semi-stratifiable space 2010 MSC;54C05;54C08;54C30;54E20;47H04
1 Introduction
All spaces are assumed to be regular spaces.
For a given pair of real-valued functions(g,h)on a spaceX,under what conditions does there exist a continuous functionfsuch thatg≤f≤h(g(x)≤f(x)≤h(x) for eachx∈X)?The resolution of the problem forms one part of the classical theory of general topology and presents some characterizations of certain spaces,such as extremely disconnected spaces,stratifiable spaces,etc.
A real-valued functiongis lower semi-continuous (upper semi-continuous)if the setsg-1((r,∞))(g-1((∞,r)))are open inXfor eachr∈.For two functionsf,f′:X→,we express byf≤f′ andf In 1917,Hahn[5] proved that the necessity in Theorem 1.1 holds for metrizable spaces.Dieudonné[2]later proved that Hahn’s result,and the necessity part of Theorem 1.2 hold in paracompact spaces.In fact,these so called insertion results turn out to provide characterizations of natural and important topological properties as the following three theorems show. Theorem1.1(Katětov[6],Tong[11])A spaceXis normal if and only if for each upper semi-continuous functiong:X→and lower semi-continuous functionh:X→such thatg≤h,there is a continuous functionf:X→such thatg≤f≤h. Theorem1.2(Dowker[3])A spaceXis normal and countably paracompact if and only if for each upper semi-continuous functiong:X→and lower semi-continuous functionh:X→such thatg Theorem1.3(Michael[9])A spaceXis perfectly normal if and only if for each upper semi-continuous functiong:X→and lower semi-continuous functionh:X→such thatg≤h,there is a continuous functionf:X→such thatg≤f≤handg(x) The above results are the insertion of continuous functions for a given pair of realvalued functions(g,h) on a spaceX.In 2007,Yan and Yang[14] investigated the relations between the stratifiable structure of spaces and the insertion of semi-continuous functions as the following three theorems show. Theorem1.4(Yan,Yang[14])A spaceXis perfect if and only if for each lower semi-continuous functionh:X→such that 0≤h,there is an upper semi-continuous functionΦ(h):X→such that 0≤Φ(h)≤h,and 0<Φ(h)(x) Theorem1.5(Yan,Yang[14])A spaceXis semi-stratifiable if and only if for each lower semi-continuous functionh:X→such that 0≤h,there is an upper semi-continuous functionΦ(h):X→such that(i)0≤Φ(h)≤h,and 0<Φ(h)(x) In order to characterize thek-semi-stratifiable spaces,Yan and Yang[14]introduced the following: Theorem1.6(Yan,Yang[14])A real-valued functionfis a K-lower(K-upper)semi-continuous function if for every compact setK,fhas a minimum(maximum)value onK. Theorem1.7(Yan,Yang[14])A spaceXisk-semi-stratifiable if and only if for each lower semi-continuous functionh:X→such that 0≤h,there is an upper and K-lower semi-continuous functionΦ(h):X→such that (i)0≤Φ(h)≤h,and 0<Φ(h)(x) Definition1.8(Good,Knight,Stares[4]).A spaceXis said to be monotonically countably metacompact(MCM),if there is an operatorUassigning to each decreasing sequence(Dj)j∈wof closed sets with empty intersection,a sequence of open setsU((Dj))=(U(n,(Dj)))n∈wsuch that (1)Dn⊆U(n,Dj))for eachn∈w (2)ifDn⊆En,thenU(n,(Dj))⊆U(n,(Ej)) for eachn∈w (3)∩n∈wU(n,(Dj))=Ø. In 1965,Mack[8]proved that a spaceXis countably paracomparct if and only if for each locally bounded functionh:X→there exists a locally bounded l.s.c.functiong:X→such that |h|≤g.In 2007,Yamazaki[15] replaced the real-valued functionshandgabove by set-valued mappings(see Theorem 1.10).In order to characterize MCP and MCM with set-valued mappings,Yamazaki[15]introduced the following: Definition1.9For a spaceYhaving a countable strictly increasing closed cover{Bn},a mappingφ:X→B(Y;{Bn}) is called locally bounded if for everyx∈Xthere existn∈wand a neighborhoodOofxsuch thatO⊂φ#[Bn]. Also,Yamazaki obtained the following theorem in [15]. Theorem1.10(Yamazaki[15])For a spaceX,the following statements are equivalent: (1)Xis countably paracomparct(resp.countably metocompact); (2)for every spaceYhaving a strictly increasing closed cover{Bn},there exists an operatorΦassigning to each locally bounded mappingφ:X→B(Y;{Bn}),a locally bounded l.s.c.(resp.a l.s.c)mappingΦ(φ):X→B(Y;{Bn}) withφ⊂Φ(φ); (3)for every metric spaceYthere exists an operatorΦassigning to each locally bounded mappingφ:X→B(Y),a locally bounded l.s.c(resp.a l.s.c)mappingΦ(φ):X→B(Y) withφ⊂Φ(φ). Yamazaki[15]also proved that the statements(2′) and (3′) obtained from(2) and (3),respectively,by requiringΦa further condition “Φ(φ)⊂Φ(φ′) wheneverφ⊂φ′” are naturally equivalent to (1′)Xis MCP(resp.MCM). Along this way,in this paper,we replace the real-valued functions in Theorems 1.4,1.5 and 1.7 by set-valued mappings.And we give some characterizations of classical spaces with the insertion of set-valued mappings as well. Definition1.11(Creede[1])A spaceXis said to be semi-stratifiable,if there is an operatorUassigning to each closed setF,a sequence of open setsU(F)=(U(n,F))n∈wsuch that (1)F⊆U(n,F) for eachn∈w (2)ifD⊆F,thenU(n,D)⊆U(n,F) for eachn∈w (3)∩n∈wU(F)=F. Xis said to bek-semi-stratifiable(Lutzer[7]),if,in addition,(3′) obtained from(3)by requiring(3) a further condition ‘if compact setKsuch thatK∩F=Ø,there is somen0∈wsuch thatK∩U(n0,F)=Ø’. In this section,we discuss the relations between set-valued and real-valued semi-continuous functions.Some results will be used in the third section.In 2007,Yan and Yang[14] introduced real-valuedk-semi-continuous function to describek-semi-stratifiable spaces.We now give the definition of set-valuedk-semi-continuous function,which will be used to describek-semi-stratifiable space,as following: Definition2.1A mappingφ:X→2Ycalled K lower semi-continuous functions (K-l.s.c)andKupper semi-continuous functions(K-u.s.c),if for any compact setKinX, there isx0∈Ksuch thatφ(x0)⊂φ(x) andφ(x)⊂φ(x0),respectively,for eachx∈K. In[14],Yan and Yang obtained that every real-valued lower(upper)semi-continuous function is aKlower(upper)semi-continuous function.But for set-valued mapping,the result need not true as the following example shows. Example2.2Letφ:X→2xbe defined by φ(x)={x} for eachx∈X.It is obvious thatφis l.s.c and u.s.c,but not K-l.s.c or K-u.s.c. The following Lemma 2.3 is easy to prove,so we omit the proof. Lemma2.3For any spacesXandY,letφ:X→2Y,then (1)φis u.s.c if and only if for any closed setDinY,theφ-1[D] is closed inX; (2)φis l.s.c if and only if for any closed setDinY,theφ#[D] is closed inX; Set Ⅱ=[0,1]. Proposition2.4For any spaceXandφ:X→2Ⅱ,leth1,φ,h2,φ:X→Ⅱ defined byh1,φ(x)=supφ(x) andh2,φ(x)=infφ(x),respectively,for eachx∈X,then (1)ifφis K-u.s.c(resp.K-l.s.c),h1,φis K-u.s.c(resp.K-l.s.c); (2)ifφis K-u.s.c(resp.K-l.s.c),h2,φis K-l.s.c(resp.K-u.s.c); (3)ifφis u.s.c(resp.l.s.c),h1,φis u.s.c(resp.l.s.c); (4)ifφis u.s.c(resp.l.s.c),h2,φis l.s.c(resp.u.s.c). Proof.(1)Supposeφis K-u.s.c(resp.K-l.s.c).LetKis a compact set inX.By Definition 2.1,there isx0∈Ksuch thatφ(x)⊂φ(x0) (resp.φ(x)⊃φ(x0))for eachx∈K,soh1,φ(x)=supφ(x)≤supφ(x0)=h1,φ(x0)(resp.h1,φ(x)=supφ(x)≥supφ(x0)=h1,φ(x0)) for eachx∈K. That is,h1,φis K-u.s.c(resp.K-l.s.c)by Definition 1.6. (2)Similar to (1). (3)Supposeφis u.s.c.For everyr∈Ⅱ,{x∈X|supφ(x) Suppeoseφis l.s.c.For everyr∈Ⅱ,{x∈X|supφ(x)≤r}={x∈X|φ(x)⊂[0,r]}=φ#[[0,r]].One can easily obtain that the setφ#[[0,r]] is closed by (2) of Lemma 2.3.that is,{x∈X|h1,φ(x)≤r} is closed for eachr∈Ⅱ,soh1,φis l.s.c. (4)Supposeφis l.s.c.For everyr∈Ⅱ,{x∈X| infφ(x)≥r}={x∈X|φ(x)⊂[r,1]}=φ#[[r,1]].One can easily obtain that the setφ#[[r,1]] is closed by (2) of Lemma 2.3,that is,{x∈X|h2,φ(x)≥r} is closed for eachr∈Ⅱ,soh2,φis u.s.c. Supposeφis u.s.c.For everyr∈Ⅱ,{x∈X|infφ(x)>r}=∪n∈{x∈X|φ(x)⊂(r+,1]}=∪n∈φ#(r+,1]].One can easily obtain that the set ∪n∈φ#[(r+,1]]is open by the definition of u.s.c,that is,{x∈X|h2,φ(x)>ris open for eachr∈Ⅱ,soh2,φis l.s.c. Remark.In particular,if the mappingφ′:X→2Ⅱsuch thatφ⊂φ′,h1,φ≤h1,φ′andh2,φ′≤h2,φ. Proposition2.5.For any spaceXandh:X→Ⅱ,letφ1,h,φ2,h:X→2Ⅱby definedφ1,h(x)=[0,h(x)] andφ2,h(x)=[h(x),1],respectively,for eachx∈X,then (1)ifhis K-u.s.c(resp.K-l.s.c),φ1,his K-u.s.c(resp.K-1.s.c); (2)ifhis K-u.s.c(resp.K-l.s.c),φ2,his K-l.s.c(resp.K-u.s.c); (3)ifhis u.s.c(resp.l.s.c),φ1,his u.s.c(resp.l.s.c); (4)ifhis u.s.c(resp.l.s.c),φ2,his l.s.c(resp.u.s.c). Proof.(1)Suppose thathis K-u.s.c(resp.K-l.s.c),Kis a compact set inX.By Definition 1.6,there isx0∈Ksuch thath(x)≤h(x0)(resp.h(x)≥h(x0)) for eachx∈K,soφ1,h(x)=[0,h(x)]⊂[0,h(x0)]=φ1,h(x0)(resp.φ1,h(x)=[0,h(x)]⊃[0,h(x0)]=φ1,h(x0))for eachx∈K.That is,φ1,his K-u.s.c(resp.K-l.s.c)by Definition 2.1. (2)Similar to (1). (3)We only prove the case ofhbeing u.s.c,since the case ofhbeing l.s.c is similar tohbeing u.s.c. (4)Similar to (3). Remark.In particular,ifh′:X→Ⅱ such thath≤h′,φ1,h⊂φ1,h′andφ2,h⊃φ2,h′. In this section,we characterize semi-stratifiable spaces and so on by the insertion of set-valued mappings.The results are similar to Theorem 1.10. For a metric space (Y,ρ),a not empty closed setDinYhas the property (G) ifBρ(D,ε)-D≠Ø for anyε>0 and there existsε0>0 such thatBρ(D,ε0)⊂Vfor any open setVwith containingDinY; For a spaceY,a strictly decreasing closed sequence {En}n∈wwith not empty intersection has the property (G) if there existsn0∈wsuch thatEn0⊂Vfor any open setVcontaining ∩n∈wEninY. A(metric)spaceYis calledε-suitable(D-suitable)if there exists a strictly decreasing closed sequence {En}n∈whaving not empty intersection and the property (G) (a not empty closed setDhaving the property(G)). In order to be convenient,we introduce the following: Definition3.2.For aε-suitable spaceY,we call a mappingφ:X→LB(Y,{En})being(strictly)lower-bounded (with respect to {En}),if,for eachn∈w,there existn0∈wsuch thatEn0⊂φ(x) for eachx∈X-φ#[En](for eachn∈w,En⊂φ(x)for eachx∈X-φ#[En]). Theorem3.3.For a spaceX,the following statements are equivalent: (1)Xis a perfectly normal(resp.perfect); (5)there exist operatorsΦandψ(resp.there exists an operatorΦ)assigning to each l.s.c mappingg:X→Ⅱ,an u.s.c mappingΦ(g):X→Ⅱ and a l.s.c mappingψ(g):X→Ⅱ(resp.an u.s.c mappingΦ(g):X→Ⅱ)such that 0≤ψ(g)≤φ(g)≤g(resp.0≤φ(g)≤g) and 0<φ(g)(x)≤Φ(g)(x) Note:(1)⟺(5) sees Theorem 1.4 and [13]. Before we prove Theorem 3.3,let us note the following: Theorem3.4.(Xie and Yan[13])For any topological spaceX,the following statements are equivalent: (1)the spaceXis perfect; (2)there is an operatorUassigning to each decreasing sequence of closed sets(Fj)j∈w,a decreasing sequence of open sets(U(n,(Fj)))n∈wsuch that (i)Fn⊆U(n,(Fj)) for eachn∈w; (ii)∩n∈wU(n,(Fj))=∩n∈wFn; The statement(2)′ obtained from(2)by requiringUa further condition ProofofTheorem3.3.We only prove the statments for perfectly normal space.(1)⟺(5) had been proved in[13],so we only need prove(1)⟺(2)⟺(3)⟺(4)⟺(5) SetU(-1,{φ#[En]})=X,whereji=min{j∈w|j≥iandEj⊂φ(x) for eachx∈X-{φ#[Ei]}}.According toφbeing lower-bounded (with respect to {En}),the definitions ofΦ(φ) andψ(φ)are reasonable.We assert that the operatorsφandψsatisfy the conditions of (2). Finally,we will showΦ(φ) andψ(φ) to be an u.s.c mapping and a l.s.c mapping,respectively,for each lower-bounded (with respect to{En})l.s.c mappingφ:X→LB(Y,{En}). Firstly,we will showΦ(φ) to be an u.s.c mapping.Take any open setVinY.If ∩n∈wEnV,Φ(φ)#[V]=Ø,because ofΦ(φ)(x)⊃∩n∈wEnfor eachx∈X.Also,Φ(φ)#[V] is open inX.If ∩n∈wEn⊂V,there existsn0∈wsuch thatEn0⊂VandEn0-1V(setE-1=Y)according to {En}n∈whaving the property(G).Then we assert thatΦ(φ)#[V]=U(jn0,{φ#[En]}),wherejn0=min{j∈w|Φ(φ)(x)⊂En0,∀x∈U(j,{φ#[En]})}.Firstly,we will show {j∈w|Φ(φ)(x)⊂En0,∀x∈U(j,{φ#[En]})}≠Ø,that isn0∈{j∈w|Φ(φ)(x)⊂En0,∀x∈U(j,{φ#[En]})}.Take anyx∈U(n0,{φ#[En]}}),thenΦ(φ)(x)⊂Ein0+1+1⊂En0+1⊂En0⊂V,wherein0+1=min{i∈w|i≥n0+1 andEi⊂φ(x) for eachx∈X-φ#[En0+1]} according to the definition ofΦ(φ).Hence,U(jn0,{φ#[En]})⊂Φ(φ)#[V] is clear.Take anyx∉U(jn0,{φ#[En]}).We haveΦ(φ)(x)⊃Ein0+1+1according to the definition ofΦ(φ),whereijn0=min{j∈w|j≥jn0andEj⊂φ(x) for eachx∈X-φ#[Ejn0]},andEijn0+1En0.If not,we assumeEijn0+1⊂En0,then we can getΦ(φ)(x)⊂Eijn0+1⊂Ejn0for eachx∈U(jn0-1,{φ#[En]}),sojn0-1∈{j∈w|Φ(φ)(x)⊂En0,∀x∈U(j,{φ#[En]})},which is a contradiction withjn0=min{j∈w|Φ(φ)(x)⊂En0,∀x∈U(j,{φ#[En]})}.Hence for anyx∉U(jn0,{φ#[En]}),Φ(φ)(x)⊃Eijn0+1En0,that isΦ(φ)(x)⊃Eijn0+1⊃En0.Furthermore,we haveΦ(φ)(x)V,because ofEn0-1V.So we complete the proof of our assertionΦ(φ)#[V]=U(jn0,{φ#[En]}),wherejn0=min{j∈w|Φ(φ)(x)⊂En0,∀x∈U(j,{φ#[En]})}.In all,Φ(φ)#[V] is an open set inXfor any open setVinY,soΦ(φ) is u.s.c. Now we will showψ(φ) to be a l.s.c mapping. Take any closed setDinY.If ∩n∈wEnD,ψ(φ)#[D]=Ø,because ofψ(φ)(x)⊃∩n∈wEnfor eachx∈X. Also,ψ(φ)#[D] is closed inX.If ∩n∈wEn⊂D,(a)if there is non0∈wsuch thatEn⊂D,ψ(φ)#[D]=∩n∈wφ#[En]=according to the definition ofψ(φ), soψ(φ)#[D] is closed inX.(b)if there isi0∈wsuch thatEi0⊂D,there existsn0∈wsuch thatEn0⊂DandEn0-1D(setE-1=X).Then using the same way above we can getψ(φ)#[D]=,wherejn0=min{j∈w|ψ(φ)(x)⊂En0,∀x∈,soψ(φ)#[D] is closed inX.Because of closed setDbeing any taken,ψ(φ)is a l.s.c mapping according to (2) of the Lemma 2.3. (3)⟺(4).We only note that the closed set {0} having the property (G) and Ⅱ is metric,and apply(3). Theorem3.5.For a spaceX,the following statements are equivalent: (1)Xis stratifiable (resp.semi-stratifiable); (5)there exist operatorsΦandψ(resp.there exissts an operatorΦ)assigning to each l.s.c mappingg:X→Ⅱ,an u.s.c mappingΦ(g):X→Ⅱ and a l.s.c mappingψ(g):X→Ⅱ(resp.an u.s.c mappingΦ(g):X→Ⅱ)such that (i) 0≤ψ(g)≤Φ(g)≤g(resp.0≤Φ(g)≤g) and 0<ψ(g)(x)≤Φ(g)(x) Note(1)⟺(5) sees Theorem 1.5 and [13,Theorem 3.5]. Before we prove Theorem 3.5,let us note the following: Theorem3.6.(Xie and Yan[13]For any topological spaceX,the following statements are equivalent: (1)spaceXis semi-stratifiable; (2)there is an operatorUassigning to a decreasing sequence of closed sets (Fj)j∈w,a decreasing sequence of open sets (U(n,(Fj)))n∈wsuch that (a)Fn⊆U(n,(Fj)) for eachn∈w; (b)∩n∈wU(n,(Fj))=∩n∈wFn; ProofofTheorem3.5.We only prove the statements forXbeing stratifiable. (1)⟺(5)had been proved in[13],so we only need prove (1)⟹(2)⟹(3)⟹(4)⟹(5). (1)⟹(2).Assume thatXis stratifiable and thatUis an operator satisfying (a)-(d) of (2′) in Theorem 3.6.Let spaceYhave a strictly decreasing closed sequence {En} with ∩n∈wEn≠Ø and having the property (G).For each l.s.c mappingφ:X→LB(Y,{En}) such that if,∀x∈X,φ(x)En,thenEn⊂φ(x)for anyn∈w,according to (2) of Lemma 2.3,we have {φ#[En]}n∈wbeing decreasing closed subsets inX.Set {U(i,{φ#[En]})}i∈w=U({φ#[En]}).Since spaceXis stratifiable,according to (2) of Theorem 3.6,{U(i,{φ#[En]})}i∈wis a decreasing open subsets such that=∩i∈wU(i,{φ#[En]})=∩n∈wφ#[En].We define mappingsΦ(φ)X:→LB(Y,{En}) andψ(φ)X:→LB(Y,{En}) as following: SetU(-1,{φ#[En]})=X.We assert that the operatorsΦandψsatisfy(2). Now we will show (ii)Φ(φ′)⊂Φ(φ) andψ(φ)⊂ψ(φ′) wheneverφ⊂φ′ for any pair of l.s.c mappingsφ,φ′:X→LB(Y,{En}) such that if,∀x∈X,φ(x)Ei(resp.φ′(x)Ei),Ei⊂φ(x)(resp.φ′(x)Ei) for anyi∈w.Set {U(i,{φ#{En]})}i∈w=U({φ#[En]}) and {U(i,{φ′#[En]})}i∈w=U({φ#[En]}).Sinceφ⊂φ′,φ#[En]⊃φ#[En] for eachn∈w.Furthermore,U(i,{φ′#[En]})⊃U(i,{φ#[En]}),according to the operatorUholding for (c) of (2) in Theorem 3.6,for eachi∈w. (2)⟹(3).Similar to (2)⟹(3) in the proof of Theorem 3.3. (3)⟹(4).Similar to (3)⟹(4) in the proof of Theorem 3.3. The proof of Theorem 3.7 is similar to the proofs of Theorems 3.3 and 3.5,so we omit it. Theorem3.7.For a spaceX,the following statements are equivalent: (1)Xis MCP(resp.MCM); (5)there exist operatorsΦandψ(resp.there exists an operatorΦ) assigning to each l.s.c mappingg:X→Ⅱ such that 0 Note.The (1)⟺(5) was proved in [15]. Lemma3.8.For any topological spaceX,the following statements are equivalent: (1)spaceXisk-semi-stratifiable; (2)there is an operatorUassigning to a decreasing sequence of closed sets (Fj)j∈w,a decreasing sequence of open sets(U(n,(Fj)))n∈wsuch that (b)for any compact subsetKinX,if ∩n∈wFn∩K=Ø,there isn0∈wsuch thatU(n0,(Fj))∩K=Ø; Proof.(1)⟹(2)LetU0be an operator having the properties:(1),(2) and (3′) in Definition 1.11.Given any decreasing sequences of closed sets(Fj)j∈w,we can define an operatorUby U((Fj))=(U(n,(Fj)))n∈wwhereU(n,Fj))=U0(n,F0) for eachn∈w We shall prove that the operatorUhas the properties (a)-(c) in (2).Because ofU0having properties (1) and (2) in Definition 1.11,one can easily verify thatUhas the properties(a) and (c) in (2).We show that the property(b) in (2)holds forU.Take any decreasing sequences of closed sets (Fn)n∈wand any compact subsetKinXsuch that ∩n∈wFn∩K=Ø.Then,there existsn0∈wsuch thatFn0∩K=Ø.SinceXisK-semi-stratifiable,there isi∈wsuch thatU0(i,Fn0)∩K=Ø.Ifi (2)⟹(1)LetU0be an operator having the properties (a)-(c) in (2).Given any closed setFinXby lettingFn=Ffor eachn∈w,we can define an operatorUby U(j,F)=U0(j,(Fn)) where (U0(j,(Fn)))j∈w=U0((Fn)) One can easily verify that the operatorUhas the properties in Definition 1.11. Theorem3.9.For a spaceX,the following statements are equivalent: (1)Xisk-semi-stratifiable; (5)there exists and operatorΦassigning to each l.s.c mappingg:X→Ⅱ,an u.s.c and K-l.s.c mappingΦ(g):X→Ⅱ such that (i)0≤Φ(g)≤gand 0<Φ(g)(x) Proof.(1)⟺(5)was proved in Theorem 1.7,so we only show(1)⟹(2)⟹(3)⟹(4)⟹(5). (1)⟹(2)Suppose thatXis K-semi-stratifiable.Define an operatorΦas theΦof (1)⟹(2) in the proof of Theorem 3.5 with the operatorUsatisfying(2)in Lemma 3.8.Then we need only to show that for each l.s.c mappingφ:X→LB(Y,{En})such that if,∀x∈X,φ(x)Ei,Ei⊂φ(x)for anyi∈w,Φ(φ) is K-l.s.c.Assume thatKis a not empty compact set inX.If ∩n∈wφ#[En]∩K=Ø,byXbeingk-semi-stratifiable and Lemma 3.8,there isi0∈wsuch thatU(i0,{φ#[En]})∩K=Ø for alln≥i0whileU(n-1,{φ#[En]})∩K≠Ø for alln≤i0(setU(i0-1,{φ#[En]}=X).Takex0∈K∩U(i0-1,{φ#[En]}).Then for eachx∈Kthere existsj0such thatx∈U(j0-1,{φ#[En]})-U(j0,{φ#[En]}) andj0≤i0.Hence,according to the definition ofΦ(φ),we can getΦ(φ)(x)=Ej0+1⊃Ei0+1=Φ(φ)(x0);If∩n∈wφ#[En]∩K≠Ø,takingx0∈∩n∈wφ#[En]∩K,we have,for anyx∈K,Φ(φ)(x0)=∩n∈wEn⊂Φ(φ)(x)accordingx0∈∩n∈wφ#[En]=∩i∈wU(i,{φ#[En]}) and the definition ofΦ(φ).So we complete the proof ofΦ(φ)being K-l.s.c. (2)⟹(3) Similar to (2)⟹(3) in the proof of Theorem 3.3. (3)⟹(4) Similar to (3)⟹(4) in the proof of Theorem 3.3. (4)⟹(5) Assume that (4).Define an operatorΦas theΦof (4)⟹(5) in the proof of Theorem 3.5.Then we need only to show that for each l.s.c mappingg:X→Ⅱ,Φ(g) is real-valued K-l.s.c.One can easily obtain thatΦ(g) is real-valued K-l.s.c.according to (1)in Proposition 2.4.In 2003,Peng and Lin[10] gave thekβ(see[12])characterization as following.They renamed thekβask-MCM in[10]. Theorem3.10.(Peng,Lin[10])For a spaceX,the following statements are equivalent: (1)Xisk-MCM (2)there is an operatorUassigning to a decreasing sequence of closed sets (Fj)j∈wwith ∩j∈wFj=Ø,a decreasing sequence of open sets (U(n(Fj)))n∈wsuch that (a)Fn⊆U(n,(Fj))for eachn∈w; (b)for any compact subsetKinX,there isn0∈wsuch thatU(n0,(Fj)))∩K=Ø; (c)given two decreasing sequences of closed sets (Fj)j∈wand (Ej)j∈wsuch thatFn⊆Enfor eachn∈wand that ∩j∈wFj=∩j∈wEj=Ø,thenU(n,(Fj))⊆U(n,(Ej)),for eachn∈w. Theorem3.11.For a spaceX,the following statements are equivalent: (1)Xisk-MCM; (5)there exists an operatorΦassigning to each l.s.c mappingg:X→Ⅱ such that 0 Proof.(1)⟹(2).Suppose thatXisk-MCM and thatUis an operator satisfying (a)-(c)of (2)in Theorem 3.10.Let spaceYhave a strictly decreasing closed sequence {En} with ∩n∈wEn≠Ø and having the property(G).For each l.s.c mappingφ:X→LB(Y,{En}) such that if,∀x∈X,φ(x)En,En⊂φ(x) for anyn∈wand that ∩n∈wEnφ,according to (2) of Lemma 2.3, we have {φ#[En]}n∈wbeing decreasing closed subsets such that ∩n∈wφ#[En]=Ø inX.Set {U(i{φ#[En]})}i∈w=U({φ#[En]}).Since spaceXisk-MCM,according to (2) of Theorem 3.10,{U(i,{φ#[En]})}i∈wis a decreasing open subsets satisfying (a)-(c) of (2) in Theorem 3.10.We defineΦ(φ):X→LB(Y,{En}) as following:Φ(φ)(x)=Ei+1,x∈U(i-1,{φ#[En]})-U(i,{φ#[En]}).(SetU(-1,{φ#[En]})=X) The proofs ofΦ(φ)being u.s.c and satisfying (i) and (ii) in (2) are similar to the proof of ‘(1)⟹(2)’ in Theorem 3.5.So we need to show thatΦ(φ) is K-l.s.c for each l.s.c mappingφ:X→LB(Y,{En}) such that if,∀x∈X,φ(x)Ei,Ei⊂φ(x) for anyi∈wand that ∩n∈wEnφ. Assume thatKis a not empty compact set inX.ByXbeingk-MCM and (b) of (2) in Theorem 3.10,there isi0∈wsuch thatU(i0,{φ#[En]})∩K=Ø for alln≥i0whileU(n-1,{φ#[En]})∩K≠Ø for alln≤i0(setU(i0-1,{φ#[En]}=X).Takex0∈K∩U(i0-1,{φ#[En]}).Then for eachx∈Kexistsj0such thatx∈U(j0-1,{φ#[En]})-U(j0,{φ#[En]}) andj0≤i0.Hence,according to the definition ofΦ(φ),we can getΦ(φ)(x)=Ej0+1⊃Ei0+1=Φ(φ)(x0),that implies thatΦ(φ) is K-l.s.c. (2)⟹(3)Similar to (2)⟹(3) in the proof of Theorem 3.3. (3)⟹(4)Similar to (3)⟹(4) in the proof of Theorem 3.3. (4)⟹(5)Similar to (4)⟹(5) in the proofs of Theorem 3.9 and Theorem 3.5. (5)⟹(1)According to Theorem 3.10,we only need show that there exists an operatorUsatisfying (2) in Theorem 3.10 for each decreasing closed subsets{En}n∈wwith empty intersection inX. The {U(i,{En})} being a decreasing open subsetsEi⊂U(i,{En}) is obvious,which implies that theUholds for (a). [1]G.D.Creede.Semi-stratifiable[J].IN:Proc Arizona State Univ Topological Conf,1967,1969:318~323. [2]J.Dieudonné.Une généralisation des espaces compacts[J].J.Math.Pures Appl.,1944,23:76. [3]C.H.Dowker.On countably paracompact spaces[J].Canad.J.Math.,1951,3:219~224. [4]C.Good,R.Knight,I.Stares.Monotone countable paracompactness[J].Topology Appl.,2000,101:281~298. [5]H.Hahn.Uber halbstetige und unstetige funktionen[J].Sitzungsberichte Akad Wiss.WienAbt.Ha 126. [6]M.Katěetov.On real-valued function in topological spaces[J].Fund.Math.,1951,38:85~91. [7]D.L.Lutzer.Semistratifiable and stratifiable[J].Topology Appl.,1971,1:43~48. [8]J.Mack.On a class of countably paracompact spaces[J].Proc.Amer.Math.Soc.,1965,16:467~472. [9]E.Michael.Continuous selectionsI[J].Ann.of Math.,1956,63:361~382. [10]L.X.Peng,S.Lin.On monotone spaces and matrization theorems[J].Acta.Math.Sinica,2003,46:1225~1232(in Chinese). [11]H.Tong.Some characterizations of normal and perfectly normal spaces[J].Duke Math.J.,1952,19:289~292. [12]L.S.Wu.Aboutk-semistratifiable spaces[J].J.Socow Univ.,1986,4:47~57. [13]L.H.Xie,P.F.Yan.Insertion of semi-continuous functions and sequences of sets[J].Acta Math.Hungar.,2010,126:164~180. [14]P.F.Yan,E.G.Yang.Semi-strtifiable spaces and the insertion of semi-continuous functions[J].J.Math.Anal.Appl.,2007,328:429~437. [15]K.Yamazaki.Locally bounded set-valued mappings and monotone countable paracompactness[J].Topology Appl.,2007,154:2817~2825. 集值映射与层型结构空间 谢利红,燕鹏飞 (五邑大学 数学与计算科学学院,广东 江门 529020) 本论文利用半连续集值映射的插入给出具有层型结构空间的一些等价刻画.也引入了K-lower和K-upper集值映射,利用此概念给出了k-半层空间以及k-MCM的刻画. K-upper(K-lower)集值映射;层型空间;半层空间;MCM;MCP;k-MCM(kβ);k-半层空间 梁怀学) date:2014-06-10FoundationitemSupported by the Natural Science Foundation of China(No.10971125);the Project of Department of Education of Guangdong Province(No.2012KJCX0101);the Science Foumdation for Young Teachers of Wuyi University(No.2013zk03) Biographies:Xie Lihong(1982-),male,doctor.Main research:general topology. O189.2DocumentcodeAArticleID1674-3873-(2014)03-0048-12

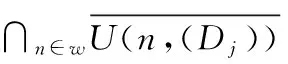
2 Set-valued and real-valued semi-continuous functions

3 Set-valued l.s.c mappings and semi-stratifiable spaces