气液两相流管流压降计算理论综述

王立佳，陈晶华

（1.海洋石油工程股份有限公司，天津 300451）

（2.中海石油（中国）有限公司北京研究中心，北京 100027）

在石油开采工业中，大量存在着气液混合物在管道中的流动运动形式。通常情况下，气井采出流体气液比高，但即便只有少量液体存在，也会对流动带来相当大的影响。油井产出物中通常含有水和天然气，其流动形态更为复杂。从早期的研究者利用室内或现场数据，提出各种两相稳态计算经验相关公式[1-3]，到上世纪80年代后，利用物理模型模拟稳态、瞬态工况进行的计算[4-10]，总体而言，研究的重点是在寻求一种更加准确、符合实际的压降计算方法，其中摩阻系数作为压降计算的重要内容，计算的准确性直接决定了压降计算的准确性。

1 气液两相管流压降计算理论

1.1 稳态相关式计算理论

早期的气—液体两相流压降计算，多数采用均相流模型，将气液两相混合物看成均匀介质，其流动的物理参数取两相介质相应参数的平均值。之后出现了采用分相流模型的计算，即假设流体为单相流体（液相或气相），计算流动压降，然后用相关式修正。这一方法的代表是Lockhart & Martinelli法[1]，并在工业上获得广泛的应用。方法如下：

显然，按照单相流体计算压降ΔPι和ΔPg后，求出X并由Lockhart-Martinelh两相流模数X～¢关系曲线图，最终求出两相流压降。从该方法可以看出，早期的管道压降计算，只考虑了与流体物性和管径的关系，没有考虑多相流管中各相间的相互作用。

1.2 半相关式—半模型理论

以Taitel和Duakler[5-6]为代表，根据对水平和接近水平的气液两相管流层状流的力学分析，在考虑相间及相与管壁间的剪切应力作用下，提出了如下力学模型：

式中：τ-剪切应力，N/m2，下标l为液体，g为气体，i为界面；S -湿周长，mx；A -管子截面或流体占有截面，m2；α-管子倾斜角，向上为正；g -重力加速度，m/s2。

该式右侧第一项为摩阻压降，第二项为重力压降。不同流态采用不同的计算公式，但都是从摩阻压降和重力压降两个方面来计算的。

1.3 机理模型理论

上世纪80年代后，引入了核工业中用于研究蒸汽/水两相流的物理模型方法，使两相流研究获得了新的进展。欧美等国相继建立了测量手段先进的实验环道，建立了更为精确的力学模型用来描述多相流流动规律[7-10]。挪威工业研究会经过多年的合作研究，以双流体模型的水力学质量、动量、能量方程为基本方程，建立了稳态、瞬态多相流模型，开发了相应的模拟软件OLGA。并结合实验获得的水力、热力学相关式使机理方程封闭。

2 摩阻系数计算模型

两相流水力计算中，压降计算是确定多相管流管径、泵和终端分离器大小的基础，因此准确计算沿线压降具有重要意义。而沿程摩阻系数是压降计算的重要内容，其计算的准确性直接决定了压降计算的准确性，因此有必要对摩阻系数计算方法进行分析。

2.1 泰特尔—杜克勒方法[5]

式中，fi、fg、fl分别为气液界面、气相、液相的范宁系数。

2.2 Xiao等人方法

Xiao等人[7]将流型分为分层流（分层光滑流和分层波状流）、段塞流、环状流和分散泡状流四种流型，并将摩阻系数划分为流体与管壁之间的摩阻系数和气液界面摩阻系数两种，进行了不同的定义。

2.2.1 流体与管壁间摩阻系数

认为两相管流中，气体或液体与管壁之间的沿程摩阻系数的计算可以采用单相流体沿程摩阻系数的计算方法。

(1)分层流、环状流和段塞流：计算方法与单相液体管道相同，分为层流区Ⅰ、层流与紊流之间的过渡区Ⅱ、紊流光滑区Ⅲ、混合摩擦区Ⅳ、紊流粗糙区Ⅴ。

(2)分散泡状流：流型为分散泡状流时，气液两相之间没有滑动，与管壁接触的流体只有液体，故Re需用气液混合物的平均雷诺数替代。式中： Hι为持液率 ，；具体摩阻系数计算方法同(1)中的分层流、环状流和段塞流算法。

2.2.2 气液界面的摩阻系数

由于分散泡状流被看作单相流体，无需气液界面摩阻系数的计算，Xiao等人结合Andritsos和Baker的方法，提出了计算λi的新方法。

(1)分层流：首先，采用Baker等提出的方法计算εi：

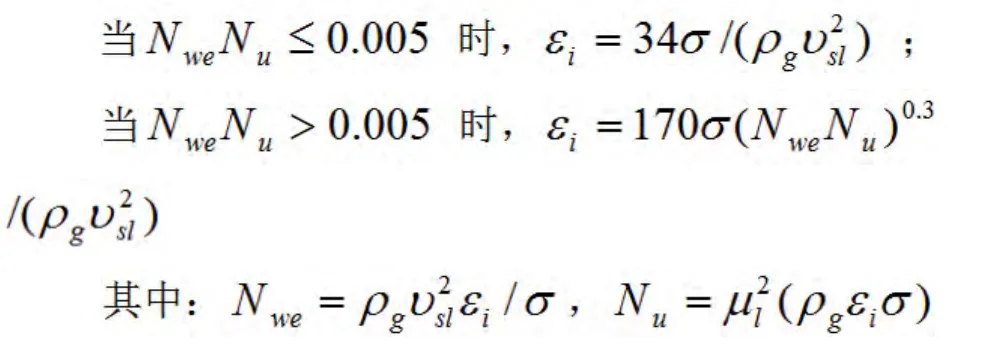
式中：εi-气液界面的相对粗糙度，其值在ε～0.25 (hl/D) 之间；Nwe、Nu-分别为韦伯数和液相黏度准数，无量纲；σ-表面张力，N/m。

将εi代入Chen氏表达式计算λi，如下：

(2)段塞流、环状流

采用Oilemans关系式计算环状流中气芯与液膜界面的沿程摩阻系数λi，忽略液体挟带率，则λi的计算如下：

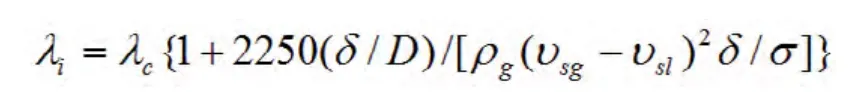
式中：λc-气芯摩阻系数；δ-液膜厚度

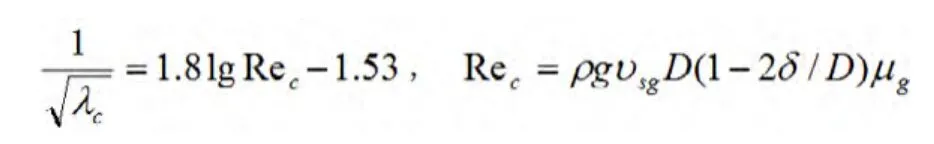
可以看出Xiao等人的摩阻系数划分方法，更加系统和准确，同时结合Andritsos、Baker、Oilemans等人的关系式对气液界面摩阻系数进行了定义。总体而言，是目前公认的准确性较强适用性较广的方法。

3 结论

综上所述，两相流计算理论的进展，经历了从借用单相流体层流计算方法的简单计算，到依据两相流流型，定义不同流型下计算方法的进步，直至目前，又将其分为流体与管壁及与气液界面的相互作用，并依据流动形态进行更为准确的计算。

同时也应看到，不论是哪种相关式或计算理论，摩阻系数的计算均采用了多种不同的假设和近似推算，究其根源，因多相管流中的相互作用，不仅存在于气体、液体与管壁之间，同时气液界面之间还存在质量交换和能量交换，这种相互作用是非常复杂的。两相流计算理论需要发展，摩阻系数的准确计算是必不可少的组成部分。新的摩阻系数计算方法的提出，必将推动两相流计算理论向更高水平的发展。

[1]陈家琅. 石油气液两相管流[M].北京：石油工业出版社，1989.

[2]冯叔初等. 油气集输[M].东营：石油大学出版社，1988.

[3]杨嘉羚，景建庄等. 长距离油、气、水管道混输系统[J].油气储运，1996，

[4]K.H.Bendlksen, D.Malnes, etc.The Dynamic Two-Fluid Model OLGA:Theory and Application, SPE Production Engineering,1991.

[5]Y.Taitel, N.Lee, A.E.Dukler, Transient Gas–Liquid Flow in Horizontal Pipes: Modeling the Flow Pattern Transitions. AIChE Journal, 1978, 24 (5):920–934.

[6]M.J.LANDMAN, Non-unique holdup and pressure drop in twophase stratified inclined pipe flow, Int. J. Multiphase Flow1997,17(3):377-394.

[7]J.J.Xiao, B.Brill, A Comprehensive Mechanistic Model For Two Phase Flow in Pipelines, 1990, SPE20631:167-180.

[8]喻西崇，冯叔初. 多相管流中沿程摩阻系数分析[J].油气田地面工程，2001，20(2)：17-21.

[9]R.I., Issa, M.H.W.Kemp, Simulation of Slug Flow in Horizontal and Nearly Horizontal Pipes with the Two-Fuid Model. Int. J. of Multiphase Flow, 2003, 29(3): 69-95.

[10]K.Yan, D.F.Che. A Coupled Model for Simulation of the Gas–Liquid Two-Phase Flow with Complex Flow Patterns. Int. J. of Multiphase Flow, 2010,36(6): 333-348.

[11]刘德生，徐孝轩. 水平管油气水三相流动规律研究进展[J].石油和化工设备，2013，16(1)：5-9.