一类具多比例时滞细胞神经网络的全局指数稳定性

赵山崎，周立群

（天津师范大学数学科学学院，天津 300387）

一类具多比例时滞细胞神经网络的全局指数稳定性

赵山崎，周立群

（天津师范大学数学科学学院，天津 300387）

通过构造合适的Lyapunov泛函和运用Halanay时滞不等式，讨论一类具多比例时滞细胞神经网络的全局指数稳定性，得到了判定该系统平衡点全局指数稳定的一个时滞独立的充分条件.通过数值算例和仿真结果验证了所得结论的有效性.

细胞神经网络；多比例时滞；全局指数稳定性；Lyapunov泛函

自1988年Chua等[1]提出细胞神经网络（CNNs）以来，CNNs被广泛应用于模式识别、图像处理、联想记忆等领域，这些应用一般要求平衡点是唯一且稳定的.而信号传输和放大器有限次的开关都会导致系统产生时滞.在网络运行中时滞是不可避免的，它会破坏系统的稳定性，并且导致系统出现振荡、分叉和混沌等现象，从而改变系统的特性.因此对时滞神经网络的研究具有重要的理论意义和实际应用价值.目前关于时滞神经网络的各种稳定性已有广泛的研究[2-12].文献[2-6]研究了不同类型的时滞细胞神经网络平衡点的全局指数稳定性.文献[7-9]通过构造Lyapunov-Krasovskill泛函和利用线性矩阵不等式，得到了细胞神经网络的全局渐近稳定性.文献[10-12]研究了时滞细胞神经网络的鲁棒稳定性.

比例时滞是众多时滞中的一种，目前对时滞神经网络的研究主要集中于常时滞、有界变时滞、分布时滞等情况，对具比例时滞的细胞神经网络的研究相对较少.比例时滞是一种无界的时变时滞，不同于无界的分布时滞，比例时滞神经网络属于时滞微分方程的范畴，由于时滞微分方程的解析解很难求得，目前关于时滞微分方程的研究大部分集中于数值解.比例时滞细胞神经网络可以根据比例时滞因子的大小和网络运行所能允许的最大时滞来控制网络的运行时间，所以研究比例时滞细胞神经网络具有重大的意义[13-15].文献[13]利用非线性测度讨论了一类具多比例延时细胞神经网络的指数稳定性.文献[14]研究了一类具多比例时滞细胞神经网络的全局指数周期性和稳定性.本研究讨论一类具多比例时滞细胞神经网络的全局指数稳定性，通过变换将多比例时滞细胞神经网络转化成等价的变系数常时滞细胞神经网络，通过构造合适的Lyapunov泛函，得到了该系统全局指数稳定的充分条件，所得条件易于验证，并给出例子及其仿真结果验证所得结论的正确性.

1 模型描述与预备知识

考虑如下具多比例时滞的细胞神经网络模型

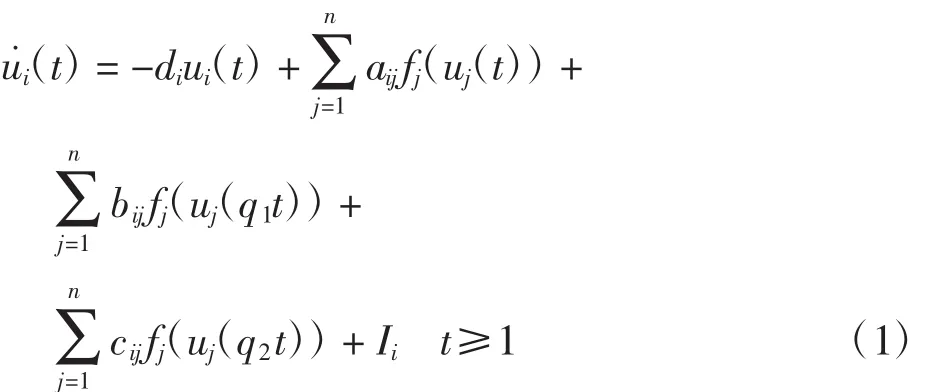
其中：i=1，2，…，n，n表示神经元的个数；di＞ 0表示在与神经网络不连通并且没有外部附加电压差的情况下第i个神经元恢复独立静息状态的速率；aij、bij、cij分别表示第j个神经元到第i个神经元在时刻t、q1t、q2t联接权的权重；q1、q2是比例时滞因子，满足0＜q1，q2＜1，qit=t-（1-qi）t，i=1，2，（1-qi）t是时变的无界时滞函数，即当t→+∞时，（1-qi）t→+∞，i=1，2；ui（t）表示第i个神经元的状态；fj（·）表示第j个神经元在时刻 t的输出，j=1，2，…，n；Ii表示第 i个神经元的偏置.

设系统（1）具有如下初始条件

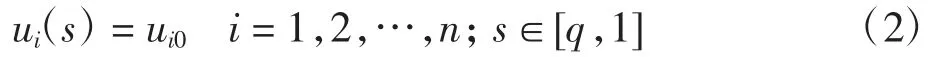
其中：ui0表示 s∈[q，1]的初始值，为常数；q=min{q1，q2}.

设系统（1）的输出函数fj（·）是Lipschitz连续的，即存在 Lj＞ 0，使得∀uj，vj∈R，有

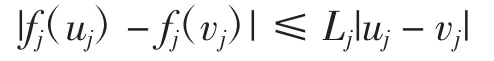
注1若fj（·）满足Lipschitz连续，那么它可以是无界的，不可微的，也可以不是单调增的.

作变换vi（t）=ui（et），则系统（1）等价地变换成如下的变系数常时滞的细胞神经网络

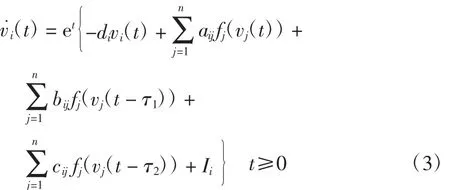
条件（2）相应地变换为

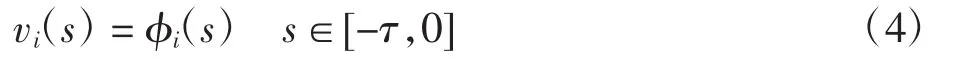
式（4）是系统（3）的初始条件，其中：τ=max{τ1，τ2}，τ1=-ln q1＞0，τ2=-ln q2＞0；φi（s）=ui0，s∈[-τ，0]，i=1，2，…，n.设 φ =（φ1，φ2，…，φn）T.

注2 容易验证系统（1）与（3）有相同的平衡点，因此要证明系统（1）平衡点的稳定性只需证明系统（3）平衡点的稳定性.

设 v*=（v1*，v2*，…，vn*）T是系统（3）的平衡点.令v（t）=（v1（t），v2（t），…，vn（t））T是异于v*的任一解，令yi（t）=vi（t）-vi*，则由系统（3）有

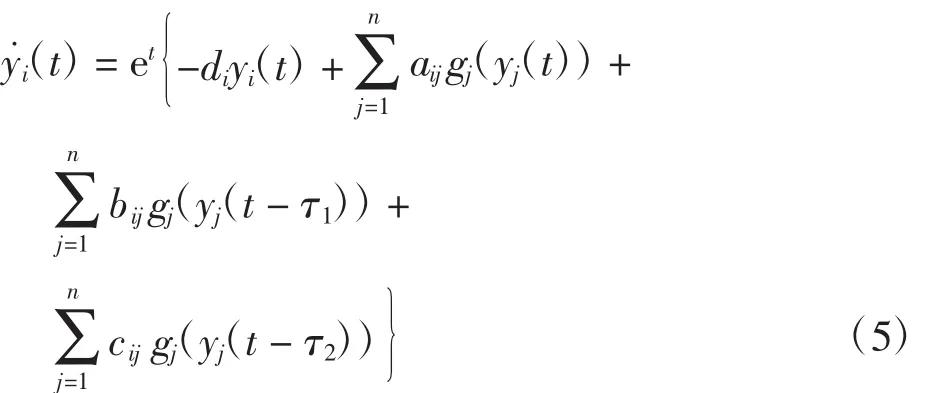
其中gj（yj（t））=fj（vj（t））-fj（vj*）.因此要证明系统（1）的平衡点的稳定性只需证明系统（5）零解的稳定性即可.

定义1 称系统（3）的平衡点是全局指数稳定的，如果存在M≥1，k＞0，使得

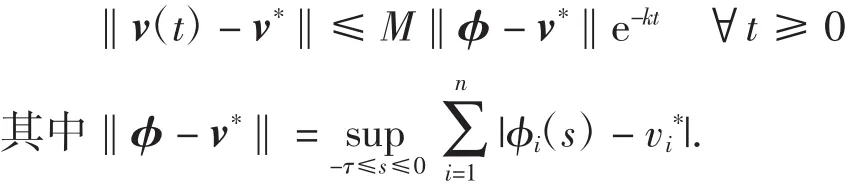
定义2 称系统（3）的平衡点是全局吸引的，如果系统（3）的平衡点v*∈Rn和任意解v∈Rn满足

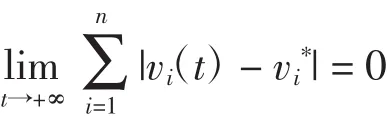
引理[2]设常数 α ＞β＞0，x（t）在 t≥ t0-τ上是非负的一元连续函数，且在t≥t0-τ上满足如下不等式

2 主要结果

定理设fj（·）为Lipschitz连续的，且存在常数λ＞1，p、q∈R，ε＞0，使得

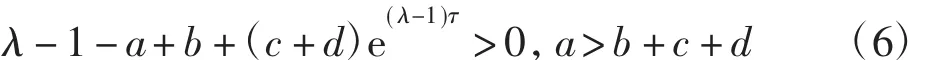
则系统（3）有唯一平衡点，并且该平衡点是全局指数稳定的.其中：

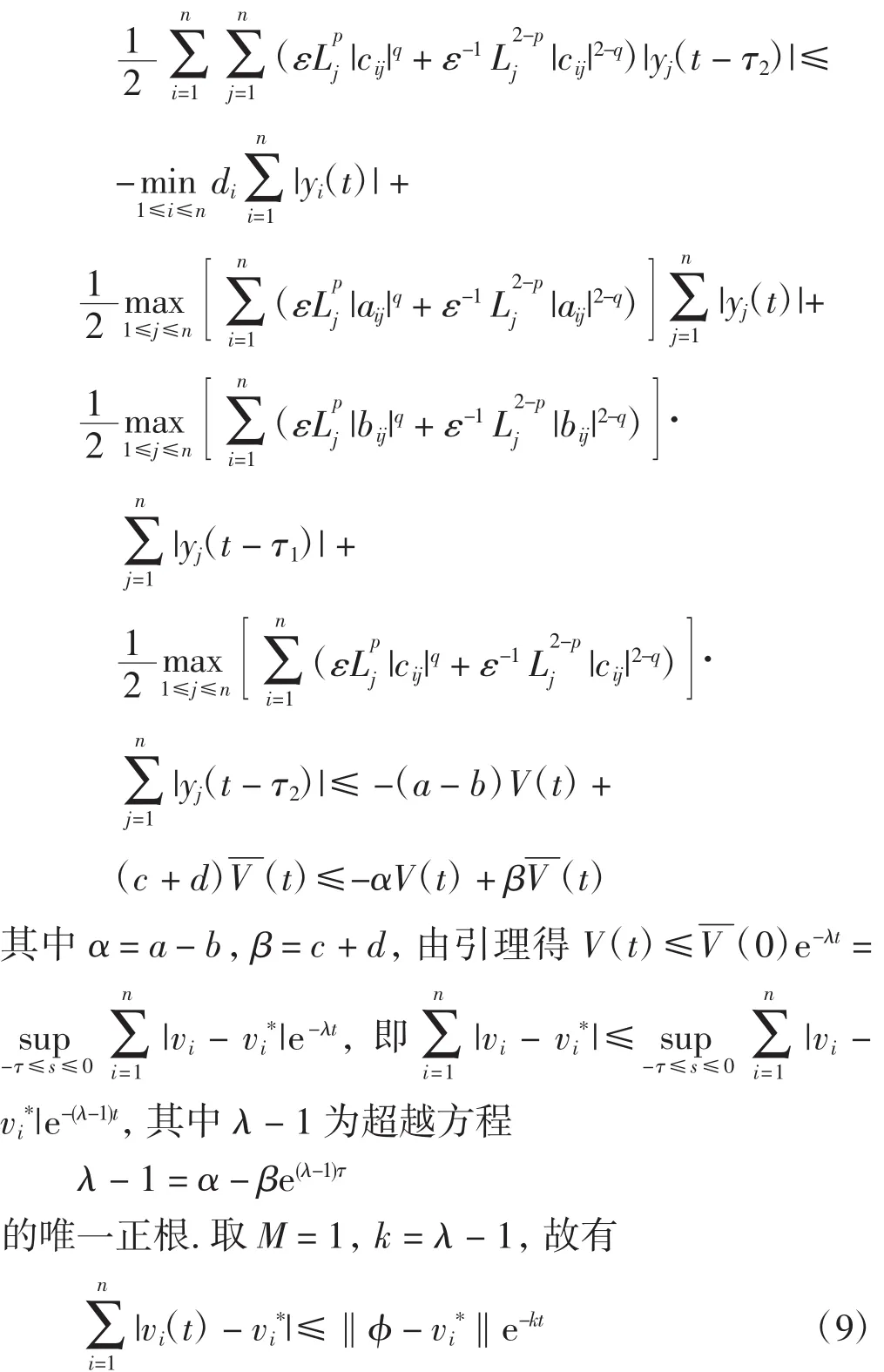
由定义1知，系统（5）的原点是全局指数稳定的，故系统（3）的平衡点是全局指数稳定且唯一的.从而系统（1）的平衡点是全局指数稳定的.

若在定理的证明过程中取p=q=1，ε=1，则可得如下推论.

推论设fj（·）为Lipschitz连续的，且

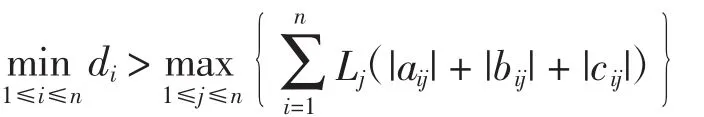
成立，则系统（1）有唯一平衡点，并且该平衡点是全局指数稳定的.

注3 推论与文献[2]中定理是一致的，但是文献[2]讨论的是具有常时滞和变时滞的CNNs的稳定性，而本研究讨论无界时变的比例时滞，因此该推论可以看作文献[2]的改进.

3 数值算例

例1 考虑如下二维神经网络

显然6=a＞b+c+d=5，满足定理的条件，故该系统存在唯一的全局指数稳定平衡点u*，利用Matlab计算，得到平衡点为 u*=（0.335 5，0.256 1）T，仿真结果见图1.

图1 例1的仿真结果Fig.1 Simulated resultsof exam ple 1

4 结论

主要讨论了一类具多比例时滞的细胞神经网络的全局指数稳定性，通过变换vi（t）=ui（et）将具多比例时滞的细胞神经网络模型变换成等价的变系数常时滞的细胞神经网络模型，通过构造合适的Lyapunov泛函和利用Halanay时滞不等式，得到了这类时滞细胞神经网络平衡点全局指数稳定的充分条件，所得条件易于验证，通过数值算例及仿真验证了结果的正确性.

[1] CHUA L O，YANG L.Cellular neural network：theory and applications[J].IEEETransCAS，1988，35（10）：1257-1290.

[2] 程晓华，张国东.一类时滞细胞神经网络的稳定性分析[J].湖北师范学院学报：自然科学版，2010，30（3）：32-35.

[3]马成荣.高阶S-分布时滞广义细胞神经网络的全局指数稳定性[J].生物数学学报，2011，26（3）：459-468.

[4] 张若军，王林山.具有分布时滞的细胞神经网络的概周期解[J].数学物理学报，2012，31（2）：422-429.

[5] 杨逢建，张超龙，吴东庆，等.具有时滞的一般型脉冲神经网络的指数稳定性[J].纯粹数学与应用数学，2011，27（1）：1-6.

[6] LIU J.Global exponential stability of cellular neural networks with time-varyingdelays[J].Math Pract Theory，2009，39（15）：194-199.

[7]莫玉忠，丁明智，虞继敏.变时滞非线性细胞神经网络稳定性分析[J].重庆邮电大学学报：自然科学版，2010，22（6）：817-822.

[8] 罗日才，许弘雷.一类中立型时滞神经网络的全局渐近稳定性[J].计算机工程与应用，2012，48（6）：30-32.

[9] 宫大为，冯建，刘金海.带有不确定的时变时滞神经网络渐近稳定性分析[J].东北大学学报：自然科学版，2010，31（3）：313-316.

[10]李亚军，邓其飞，彭云建.变时滞模糊随机细胞神经网络新的鲁棒稳定性[J].控制与决策，2011，26（8）：1197-1202.

[11]KAO Y G，GAO CC，HANW.Global exponential robust stability of reaction-diffusion interval neural networkswith continuously distributed delays[J].Neural Computing and Applications，2010，19（6）：867-873.

[12]CHENH B，ZHANGY，HU P.Noveldelay-dependent robust stability criteria for neutral stochastic delayed neuralnetworks[J].Neural Computing，2010，73（13）：2554-2561.

[13]张迎迎，周立群.一类具多比例时滞的细胞神经网络的指数稳定性[J].电子学报，2012，40（6）：1159-1163.

[14]周立群.多比例时滞的细胞神经网络的指数周期性与稳定性[J].生物数学学报，2012，27（3）：480-488.

[15]ZHOU L Q.Delay-dependent exponential stability of cellular neural net-works with multi-proportional delays[J].Neural Process Letters，DOI10.1007/s11063-012-9271-8.

G lobal exponential stability of a class of cellular neural networksw ith multi-proportional delays

ZHAO Shanqi，ZHOU Liqun
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

Global exponential stability of a class of cellular neural networks with multi-proportional delays is studied.The sufficient conditions of global exponential stability of the equilibrium of system are obtained by constructing suitable Lyapunov functional and Halanay delay inequality.An example is given to illustrate the effectiveness of the result.

cellular neural networks；multi-proportional delays；global exponential stability；Lyapunov functional

O175.13；TP183

A

1671-1114（2014）01-0007-04

2013-02-16

国家自然科学基金资助项目（60974144）；天津市高等学校科技发展基金资助项目（20100813）；天津师范大学博士基金资助项目（52LX34）

赵山崎（1989—），女，硕士研究生.

周立群（1972—），女，博士，副教授，主要从事神经网络理论及应用方面的研究.

（责任编辑 马新光）