带减振扣件的整体道床轨道横向稳定性分析*

齐少轩，刘学毅

(西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031)

目前，我国城市轨道交通大量采用具有高稳定性和高平顺性要求的无砟轨道结构。同时，由于地形条件的限制，部分城市轨道交通线路设置在小半径曲线桥梁上。例如，在建的贵阳城市轨道交通1号线，线路最小曲线半径为350 m，其中场坝村大桥位于曲线半径为450 m的小半径曲线上。在这些小半径曲线地段，特别是在曲线起讫点处，钢轨内部积蓄的温度力主要以胀轨的形式释放并伴有少许钢轨纵向爬行现象。当列车制动时，曲线起讫点处的钢轨制动力和横向位移增幅明显，由于无砟轨道整体性强，道床横向阻力大于扣件横向阻力，从而使无砟轨下基础上的无缝线路因压弯变形而失稳的可能性不大。但在列车荷载和温度荷载作用下，处于小半径曲线的无缝线路受温度压力作用而产生弯曲变形，大量连续的压弯变形不仅影响列车运行的平稳性，而且累积压弯变形超限，同样威胁行车安全，严重时甚至产生胀轨跑道等病害［1－5］。因此，根据贵阳城市轨道交通1号线小半径的线路特点，基于场坝村大桥的具体桥梁参数，简化建立钢轨－桥梁－墩台垂向耦合力学模型，采用有限元法，计算分析列车荷载、温度荷载和制动力对处于特殊桥梁段上小半径曲线段轨道稳定性的影响。

1 计算模型及参数

1．1 钢轨－桥梁－墩台垂向耦合力学模型

以贵阳城市轨道交通1号线桥上带减振扣件的整体道床轨道为例，在设计中，路基或隧道大量采用短轨枕式整体道床而桥上的整体道床采用承轨台整体道床结构并与桥梁通过门型钢筋浇筑混凝土固结连接，使整体道床和桥梁形成一个整体。因此，钢轨和整体道床的相互作用等效为线路钢轨和桥梁的相互作用。由于线路的横向对称性，取一股钢轨，建立钢轨－桥梁－墩台垂向耦合力学模型［6－9］。

模型中，钢轨和桥梁采用3D梁单元模拟;钢轨在纵向上以1/3的扣件间距划分单元，其节点与桥梁节点通过扣件垂向、纵向和横向弹簧连接，以模拟钢轨和道床垂向、纵向和横向相互作用。其中，纵向采用非线性弹簧而垂向和横向采用线性弹簧模拟;桥梁与墩台采用线性弹簧连接，以模拟墩台上的纵向力。力学分析模型如图1所示，钢轨与桥梁都在小半径曲线上，其中X方向为纵向，Y方向为横向，Z方向为垂向。

1．2 计算参数

运用有限元法通过ANSYS计算软件进行计算，参考贵阳地铁1号线场坝村大桥桥上带减振扣件整体道床实际设计参数，对带减振扣件轨道进行受力特性分析。模型总长度取610 m，其中曲线桥梁长310 m，半径450 m。为消除边界效应，模型两侧各取50 m曲线和100 m直线路基，桥梁与路基交界处仍为圆曲线，线路总圆曲线长410 m，直线和曲线路基间不设置缓和曲线。列车类型主要有2种，地铁B型车，固定轴距为2．2 m，轴重14 t，单节车长19 m，取6编组计算;地铁A型车，固定轴距为 2．5 m，轴重 16 t，单节车长 22 m，取 6 编组。制动力集度按ZK活载乘以0.164的制动力率且考虑单股钢轨换算为5．248 kN/m;地铁B型车制动力集度按B型车换算均布荷载乘以0．164的制动力率并考虑单股钢轨换算为2．416 84 kN/m;A型车制动力集度按A型车换算均布荷载乘以0.164的制动力率并考虑单股钢轨换算为2．301 754 4 kN/m，方向为左桥台至右桥台，制动长度取为310 m全桥制动。

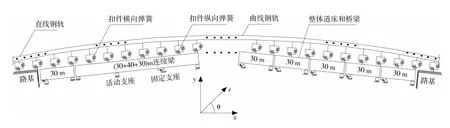
图1 曲线上钢轨－桥梁－墩台垂向耦合力学模型Fig．1 Vertical coupling model of curve rail－bridge－pier

钢轨采用CHN60钢轨;扣件选用GJ－III型减振扣件，其扣件节点的垂直静刚度为 9～14 kN/mm，本文取为9 kN/mm;无载时单组扣件防爬阻力不小于11．5 kN，经过扣件间距换算后得，取18．4 kN/m/轨，扣件横向刚度已包含扣件横向挡块的作用，并取无载时横向刚度［10］;桥梁箱梁选用C50混凝土，弹性模量为 3．45 ×104MPa，密度2 500 kg/m3，泊松比 0．2，桥台线刚度取 1 500 kN/cm/线，桥梁墩台线刚度依照设计资料取值，取为800 kN/cm/线，桥梁梁缝为0．3 m;桥梁布置形式为30 m简支梁+(30×40×30)m连续梁+6×30 m简支梁［11－13］，如图1和图2所示。根据线路实际情况施加28‰的坡度，左桥台至右桥台为顺坡，具体计算工况如表1所示。

2 曲线坡道地段特殊桥上轨道稳定性分析

2．1 温度荷载以及制动荷载对曲线轨道稳定性的影响

计算分析工况1～6，可得在温度力和制动力作用下钢轨的纵向、横向位移分布规律，如图2和图3所示。在左右桥台曲线起讫点处钢轨产生1.82 mm的横向位移，在连续梁中部钢轨有最大横向位移5．896 mm，曲线起讫点对钢轨的横向位移影响较小。如图2(b)所示，在温度力和坡度的作用下，处于坡底的曲线起讫点右桥台钢轨有最大纵向爬行0．07 mm，在连续梁中部钢轨也有较大纵向爬行0．065 mm，在施加制动荷载后，即工况4～6时，钢轨纵向爬行增幅明显，但处于坡底的曲线起讫点右桥台钢轨最大纵向爬行量仍小于0．1 mm，由此可见，在曲线地段即使作用有较大温度和制动荷载，钢轨爬行仍然较小，但钢轨胀轨位移却明显较大。

图2 不同温度荷载作用下钢轨位移规律Fig．2 Law of the rail displacement under the different temperature loads

图3 不同制动力作用下钢轨纵向位移规律Fig．3 Law of the rail longitudinal displacement under the different braking force

2．2 不同扣件横向刚度对轨道受力和变形的影响规律

计算分析工况7～9，可得在温度荷载作用下钢轨的纵向、横向位移分布规律，如图4所示。随着扣件横向刚度增大，钢轨横向位移减小，钢轨纵向爬行释放温度力使纵向位移增大，但曲线地段钢轨纵向位移仍然远小于横向位移。

图4 不同扣件横向刚度作用下钢轨位移规律Fig．4 Law of the rail displacement under the different transversal resistance of fastener

2．3 不同曲线半径对轨道受力和变形的影响规律

轨道结构其他参数不变，改变长度为410 m圆曲线的半径，取工况7的荷载组合进行计算。分别取桥梁圆曲线半径为350，450，600，800和1 000 m时，不同圆曲线半径对整体道床轨道横向受力特性的影响如表2和图5所示，其中钢轨最大横向和纵向位移发生在右桥台曲线起讫点处。

由表2和图5可知:随着圆曲线半径增大，钢轨横向和纵向位移均减小，但减小的速率随半径的增大而减缓。当轨道半径在350～450 m时，曲线半径的变化对钢轨横向和纵向位移影响大，随着半径的减小，钢轨横向和纵向位移增幅明显。当曲线半径为350 m时，钢轨横向最大位移接近8 mm达7．277 mm，已超过5 mm限值。分析计算数据可得，过小的圆曲线半径对钢轨的横向位移不利，对钢轨纵向影响也较大，但曲线上钢轨变形仍以横向变形为主。

表2 工况7下不同曲线半径对轨道结构受力和变形的影响Table 2 Influence of different curve radius on the stress and deformation of the track under the condition of seven

图5 不同桥梁圆曲线半径对钢轨位移的影响规律Fig．5 Law of the rail displacement under the different radius of bridge circular curve

2．4 不同圆曲线长度对轨道受力和变形的影响规律

轨道结构其他参数不变，改变半径为450 m，长度为310 m桥梁圆曲线的长度，分别在桥梁圆曲线两端路基地段增加圆曲线长度，当圆曲线长度为150 m，桥梁只取一半长度计算。同时取工况4的荷载组合进行计算，其中制动力仍从左桥台开始施加。分别取圆曲线长度为150，310，410，600，800和1 000 m，当圆曲线长度为150，310和410 m时，制动长度取300 m;当圆曲线长度为600，800和1 000 m时，制动长度取400 m。计算不同圆曲线长度对整体道床轨道受力和变形的影响。如表3和图6所示。

表3 不同圆曲线长度对轨道结构受力和变形特性的影响Table 3 Influence of different length of the circular curve on the stress and deformation of the track

图6 不同桥梁圆曲线长度对钢轨位移的影响规律Fig．6 Law of the rail displacement under the different length of bridge circular curve

由表3和图6可知，随着圆曲线长度增大，钢轨横向和纵向位移均增大且增幅速率随半径的增大而增加。当曲线长度在150～410 m时，曲线长度的变化对钢轨横向和纵向位移影响小，特别是曲线长度超过制动长度时，由于制动力只对作用区域一定长度范围内的钢轨有影响，因此超过制动长度的曲线长度的增加对钢轨最大横向位移几乎无影响。当曲线长度为600 m，制动长度取400 m时，制动长度超过曲线桥梁长度，在桥梁右桥台和600 m曲线起讫点处钢轨有较大横、纵向位移，曲线起讫点有最大横向位移7．029 mm，最大纵向位移0．185 6 mm。当曲线长度超过600 m时，长度的增加对钢轨横、纵向位移影响较小。分析计算数据可得，在制动长度一定的工况下，在制动长度内的曲线长度改变对钢轨横、纵向变形影响大，曲线超出制动长度后，曲线长度改变对钢轨影响较小。相较曲线长度的变化，制动长度的改变对钢轨位移和内力有明显作用。

3 结论

(1)通过改变温度荷载、扣件横向刚度以及列车制动力计算分析可得，温度荷载对曲线起讫点处钢轨受力影响大，横向变形影响较小，而列车荷载对曲线起讫点处钢轨受力影响小，横向变形影响大。

(2)随着圆曲线半径增大，钢轨横向和纵向位移均减小，但减小的速率随半径的增大而减缓。过小的圆曲线半径对钢轨的横向位移不利，对钢轨纵向影响也较大，但曲线上钢轨变形仍以横向变形为主。

(3)在制动长度一定的工况下，在制动长度内的曲线长度改变对钢轨横、纵向变形影响大，曲线超出制动长度后，曲线长度改变对钢轨影响相较偏小。相较曲线长度的变化，制动长度的改变对钢轨位移和内力有明显作用。

(4)根据《高速铁路无砟轨道线路维修规则》圆曲线最大最小正矢差不应超过5 mm可知，在工况9作用下，曲线半径为450 m，扣件横向刚度为5×107N/m的钢轨横向位移量(最大最小正矢差)为5．896 mm超过5 mm。因此，建议当圆曲线半径为450 m时，扣件横向刚度要大于5×107N/m;当扣件横向刚度为5×107N/m时，圆曲线半径要大于450 m;当扣件横向刚度为1×108N/m时，圆曲线半径要大于350 m;同时建议扣件横向刚度要大于5×107N/m，圆曲线半径大于450 mm。当圆曲线半径为450 m时，为减小制动力对曲线钢轨的影响，建议尽量减小曲线长度，缩小钢轨横向位移值。

［1］何建枝．贵阳轨道交通1号线长大连续坡道及运营安全研究［J］．都市快轨交通，2011，24(6):29－32．HE Jianzhi．Study on the safety of Guiyang Rail Transit Line 1 on continuous ramp up［J］．Urban Rail Transit，2011，24(6):29 －32．

［2］练松良，刘丽波．列车制动与道床阻力对钢轨纵向力的影响分析［J］．上海铁道大学学报，1999，20(8):75－79．LIAN Songliang，LIU Libo．The analysis of braking force and ballast resistance to the longitudinal force of rail［J］．Journal of Shanghai Railway University，1999，20(8):75－79．

［3］杨荣山，刘学毅．轨道工程［M］．北京:人民交通出版社，2012:105－116．YANG Rongshan，LIU Xueyi．Track engineering［M］．Beijing:People’s Communications Publishing，2012:105－116．

［4］曾宪海，蒋金洲．高速铁路曲线地段长大连续梁桥无缝线路方案研究［J］．铁道建筑，2011(4):1－5．ZENG Xianhai，JIANG Jinzhou．Study of CWR on the big continuous bridge in the curve section［J］．Railway Construction，2011(4):1－5．

［5］史建斌．钢轨爬行的原因分析及防治措施［J］．煤炭技术，2002，21(12):90 －91．SHI Jianbin．Cause alysis and peventive masures of the rail ceep［J］．Coal Technology，2002，21(12):91 －90．

［6］颜乐，熊震威，魏贤奎，等．坡度对长大坡道桥上无缝道岔的影响分析［J］．铁道标准设计，2013(9):33－36．YAN Le，XIONG Zhengwei，WEI Jiankui，et al．The analysis of slope to the stability of CWR on bridge with long heave grade［J］．Railway Standard Design，2013(9):33－36．

［7］王平，郭利康．线路爬行对无缝道岔受力与变形的影响分析［J］．西南交通大学学报，2002，37(6):615－619．WANG Ping，GUO Likang．The analysis of the effect of rail crawling to the force and deformation of gapless turnout［J］．Journal of Southwest Jiaotong University，2002，37(6):615－619．

［8］曲村，高亮，侯博文．城市轨道交通长大桥梁上无缝线路钢轨制动力研究［J］．城市轨道交通研究，2012(10):66－70．QU Cun，GAO Liang，HOU Bowen．The research on braking force acted on the rail of urban rail transit on long span bridge［J］．Study of City Rail Traffic，2012(10):66－70．

［9］曲村，高亮，蔡小培，等．长大简支梁桥上有砟轨道无缝线路纵横垂向变形研究［J］．铁道科学与工程学报，2012，9(5):66 －70．QU Cun，GAO Liang，CAI Xiaopei，et al．Research about longitudinal－transverse－vertical deformation of ballast CWR on long － span simply supported bridge［J］．Journal of Railway Science and Engineering，2012，9(5):66－70．

［10］张涛，张波，齐春，等．直线电机轨道工程GJ－Ⅲ型减振降噪扣件的应用［J］．铁道标准设计，2009(8):10－13．ZHANG Tao，ZHANG Bo，QQ Chun，et al．Application of GJ－Ⅲtype vibration and noise reduction fasterner on linear motor rail engineering［J］．Railway Standard Design，2009(8):10－13．

［11］刘学毅，赵坪锐，杨荣山，等．客运专线无砟轨道设计理论与方法［M］．成都:西南交通大学出版社，2010:56－67．LIU Xueyi，ZHAO Pingrui，YANG Rongshan，et al．The theory and method on ballastless track design of passenger dedicated line［M］．Chengdu:Southwest Jiaotong University Publishing House，2010:56 －67．

［12］谢国忠，袁宏姚，祖康．水泥混凝土路面最大温度梯度值［J］．华东公路，1982(6):9－19．XIE Guozhong，YUAN Hongyao，ZU Kang．The maximum temperature gradient of cement concrete pavement［J］．East China Highway，1982(6):9－19．

［13］雷俊卿，李宏年，冯东．铁路桥梁列车制动力的试验研究与计算分析［J］．工程力学，2006，23(3):134－140．LEI Junqing，LI Hongnian，FENG Dong．The computational analysis of braking force on railway bridge［J］．Engineering Mechanics，2006，23(3):134 －140．