弯剪型层模型弹塑性时程分析的若干问题*

陆铁坚，杨诗龙

(中南大学土木工程学院，湖南长沙410075)

目前，多重抗侧力体系在工程中已得到广泛应用［1－2］，多重抗侧力结构体系在水平荷载作用下的位移计算也展开了广泛研究，袁泉等［3］研究了双重弯剪型结构，童树根等［4］考虑了截面沿竖向的变化，应用串联－并联电路模型研究了双重变截面变刚度弯剪型抗侧力体系的水平位移的解析解，Lee等［5－6］研究了框架剪力墙结构的静力和动力可靠性。以上研究成果能很好地应用于规则多重抗侧力体系，如规则框剪结构、框筒结构、密肋复合墙－剪力墙混合结构等。工程实践中经常遇到复杂结构体系，为了更好地进行复杂结构体系在水平作用下的位移计算以及地震作用下的时程分析，可采用层模型来进行研究，层模型由于自由度少、求解迅速等特点，应用较广，特别是弯剪型层模型既考虑了结构的弯曲变形也考虑了剪切变形。赵西安等［7］提出了弯剪型层模型，并应用于实例;曹征良等［8］对弯剪型层模型进行了进一步研究，给出了结构总抗侧刚度矩阵。笔者认为，弯剪型层模型的弹塑性时程分析还有一些问题值得探讨。在此，就层等效抗弯刚度和等效抗剪刚度的计算，层单元刚度矩阵的推导，拐点处理等几个方面进行探讨。

1 等效抗弯刚度和抗剪刚度的计算

包世华［9］指出可用静力分析或模型试验的方法，求出结构在侧向荷载{P}作用下的侧移{x}和弯曲变形转角{θ}，然后由原结构和等效的层模型在楼层处侧移和转角分别相等的条件，折算出其等效的抗弯刚度EIi和抗剪刚度GAi。但原结构楼层处的弯曲变形转角很难由静力分析或模型试验得出，只能由水平位移的一阶导数来替代，但根据Timoshenko两广义位移梁理论可知，水平位移的一阶导数与弯曲转角不再相等［10］，其差为剪切应变。文献［7］由原结构楼层处的位移相等得到了等效抗弯刚度和抗剪刚度，适用于各层梁、柱、墙的刚度沿竖向基本均匀或变化不大的结构，为了拓宽等效EIi和GAi求解方法的应用范围，本文选取2种荷载工况{P}，如图1。使得每种荷载工况下原结构和等效层模型的水平位移都对应相等。

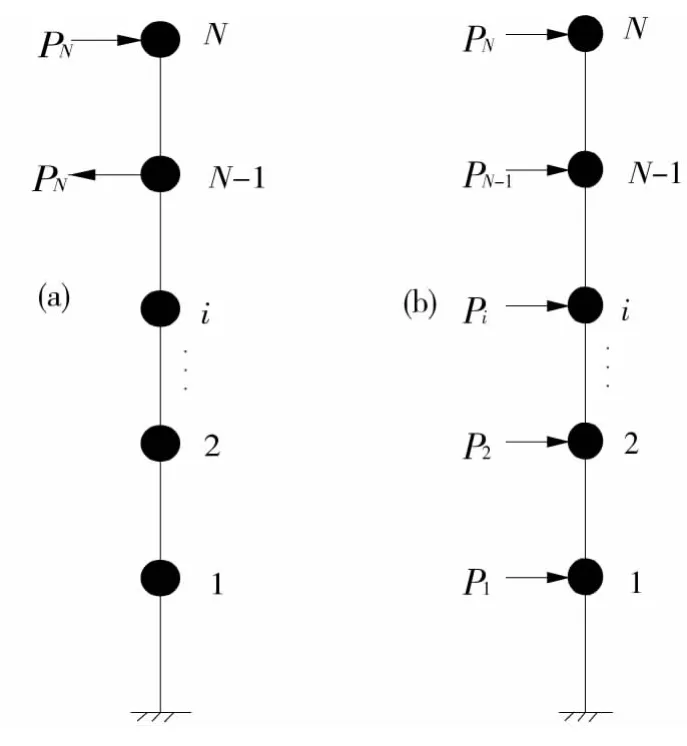
图1 2种荷载工况Fig．1 Two kinds of load condition

等效的层模型楼层处水平位移理论值的计算见下式［7］:

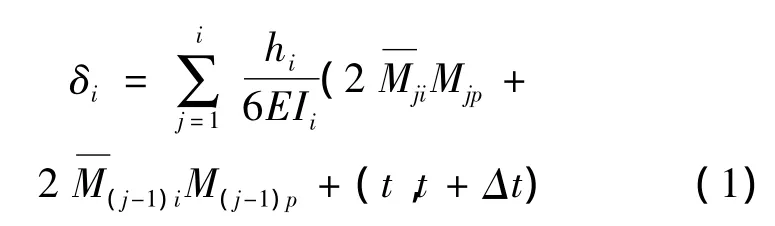
工况1下，1至N－1层仅发生弯曲变形，根据等效层模型和原结构或试验模型1至N－1层水平位移相等，可求出EI1至EIN－1，结合工况2，可得GA1至GAN－1，2工况下第N层等效层模型和原结构或试验模型分别对应相等，求出EIN和GAN。

2 层单元刚度矩阵的推导

弯剪型结构的侧向刚度矩阵一般由结构的总刚度矩阵通过缩聚的方法获得，因此先要确定结构的层单元刚度矩阵。文献［8］根据节点平衡得到了总刚度矩阵，其单元刚度矩阵实质上是考虑剪切变形的梁单元刚度矩阵，由于层模型的抗弯刚度和抗剪刚度不是实际上的EIi和GAι，而是根据楼层处水平位移相等等效计算出的等效抗弯刚度和抗剪刚度。本文采用图2所示并联电路模型计算层间位移。

图2 并联电路模型Fig．2 Parallel－ circuit model

层单元两端自由度和杆端力向量为:

xi为第i层楼层处的水平位移，θi第i层楼层处的弯曲转角。

假设虚位移为:

层间水平位移记为y(x)，则

设层间弯曲位移:

记yb(h)=yb，h为层高。

边界条件有:

由式(7)可以解出 a1，a2，a3和 a4。

设i质点相对于i－1质点的剪切位移为ys。

则根据Timoshenko剪切梁的弯曲变形与剪切变形的基本关系［11］，即图2并联模型中的电压1等于电压2，有:

将式(6)代入式(8)得:

又由图2模型可知:

将式(9)代入式(10)有:

层间剪力为:

剪切变形能为:

弯矩为:

弯曲应变能:

总势能为:

由式(19)知，弯剪型层模型的层刚度矩阵即为考虑剪切变形的Timoshenko梁单元刚度矩阵。

3 拐点处理

进行弹塑性时程分析时需要引入恢复力模型，折线型恢复力都存在转折点，即拐点。拐点前后结构或构件的刚度发生变化，为防止误差积累而严重影响解的精度，需处理好拐点问题。目前最常用的处理方法是:先计算t和t+Δt时刻结构的响应，根据两时刻的位移和速度判断是否有拐点存在，若有拐点，则计算拐点出现时刻t+Δt0。以拐点出现时刻为分界点，分成更小的步长，依次对不同刚度状态进行计算，求得其响应。因此需要计算拐点出现时刻。肖明葵等［12］提出的拐点精确计算方法，用于单自由度体系很方便，但用于多自由度体系的拐点处理较困难。文献［8］采用线性插值方法搜索拐点，线性插值法假设(t，t+Δt)时间段内位移线性变化，通过线性插值求得拐点出现时刻。但拐点前后结构刚度发生变化，位移线性变化假设误差较大，所以线性插值法将影响解的精度。现推导用于多自由度体系的拐点精确处理公式。

一般的，结构的动力反应增量方程为:

注意到，层间位移、层间速度、层间加速度与相对地面位移、速度、加速度有如下关系:

将式(21)代入式(20)，得基于层间动力状态参数的动力增量方程为:

当结构状态未发生变化时，{ΔP}=0。

对于加载点的拐点，即第1类、第3类拐点，出现拐点的楼层在拐点时刻层间位移为已知值。对于卸载点拐点，即第2类拐点，层间位移为0时出现拐点。

设拐点在(t，t+Δt)时间段出现，时刻为t+Δt0，显然0 ＜ Δt0＜ Δt。在(t，t+ Δt0)时间段内，对于加载点，根据Newmark－β法有:

将式(23)、(24)代入式(22)得:

其中:

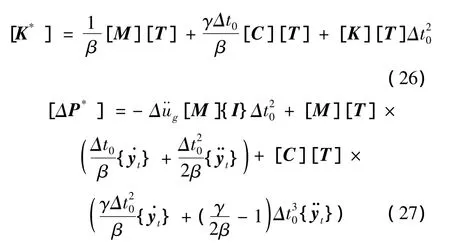
解方程(25)并整理得:

式中:

对于卸载点，若第i层出现卸载点拐点，则第i层的层间速度为0。根据Newmark－β知:

则有:

同理可以得到卸载点拐点计算公式，同式(28)。此时各系数列向量为:

以上推导了拐点计算公式的一般式，该公式以基于层间状态参数的动力方程为基础，不引入新的假设。给出的系数列阵中，只含有t时刻的状态参数和拐点出现时刻的位移或速度参数，若第i层出现拐点，则A(i)，B(i)，C(i)，D(i)，E(i)均为已知值，代入拐点计算公式方程(式(28))，即可求解出Δt0，满足0＜Δt0＜Δt的最小解即为拐点出现时刻。适用于wilson－θ法的拐点计算公式同理可以推导。

4 算例

对文献［8］中9层框架结构，采用MATLAB编制程序，进行弹塑性时程分析，结构的计算参数见表1。地震波选用Elcentro波，最大地面加速度调整为 200 gal，积分步长为 0．02 s，阻尼比采用0.05。

时程分析的计算结果的对比见表2。

由表2计算结果可知:与其他计算结果相比，本文计算的楼层底部(1～6层)的最大楼层位移偏大，而楼层上部(7～9层)的最大楼层位移值偏小;从最大层间位移来看，底下2层的最大层间位移偏大，中间层最大层间位移相差不大，顶上2层的最大层间位移偏小。特别是第2层为薄弱层，与其他方法计算结果值相比，本文计算的最大层间位移明显偏大。原因在于线性插值法处理拐点时，引入了位移线性变化假设，而实际上位移绝非线性变化，而且没有处理卸载点拐点，故其精度是较低的。

表1 9层框架结构计算参数Table 1 Parameters of frame structure of 9 storeys

表2 计算结果比较Table 2 Comparison of calculated result

5 结论

(1)本文介绍的2种荷载工况，能用于求解弯剪型层模型等效抗弯刚度和抗剪刚度。且不同楼层之间的等效抗弯刚度和抗剪刚度是彼此独立的，因此对于刚度沿楼层变化较大的结构也适用。

(2)基于势能驻值原理推导的层单元刚度矩阵是正确可行的，且易于编程。

(3)进行弹塑性时程分析时，计算精度在很大程度上取决于拐点处理方法，特别是薄弱层的最大层间位移随拐点处理方法的不同而有较大差异。本文推导的拐点精确处理公式，直接基于拐点出现时刻的动力方程，而未引入假设条件，故其精度是可靠的。且适用于剪切型层模型的拐点处理。

［1］Serrette R．Seismic design strength of cold－formed steel－ framed shear walls［J］．Journal of Structural Engineering，ASCE，2010，136(9):1123－1130．

［2］翁赟，童根树．非等高双重弯剪型抗侧力体系的稳定性［J］．工程力学，2013，30(2):65－71．WENG Yun，TONG Genshu．The stability of the dual flexural－shear substructure system with different heights［J］Engineering Mechanics，2013，30(2):65 －71．

［3］袁泉，郭猛．倒三角形荷载下双重弯剪型结构的位移计算方法［J］．应用力学学报，2013，30(1):54－58．YUAN Quan， GUO Meng． Displacement calculation method of the dual flexural－shear structure subjected to inverted triangular load［J］．Chinese Journal of Applied Mechanics，2013，30(1):54－58．

［4］童根树，赵钦．变刚度多重抗侧力结构的串并联模型［J］．浙江大学学报(工学版)，2011，45(8):1435－1440．TONG Genshu，ZHAO Qin．A series－parallel－circuit model for multiple shear－flexural structures with varied rigidities over height［J］．Journal of Zhejiang University(Engineering Science)，2011，45(8):1435－1440．

［5］Lee Seung Y，Haldar A．Reliability of frame and shear wall structural systems．Ι:Static loading［J］．Journal of Structural Engineering，2003，129(2):224－232．

［6］Lee Seung Y，Haldar A．Reliability of frame and shear wall structural systems．Ⅱ:Dynamic loading［J］．Journal of Structural Engineering，2003，129(2):233 －240．

［7］赵西安，钱庾青．高层建筑结构分层模型弹塑性动力分析［J］．固体力学学报，1982(3):442－448．ZHAO Xi’an，QIN Yuqing．Multimass system for dynamic response analysis of tall building structures［J］．Acta Mechanica Solida Sinica，1982(3):442－448．

［8］曹征良，洪翔，吴兵．层间弯剪型高层结构的弹塑性地震反应分析［J］．深圳大学学报理工版，2004，21(2):116－122．CAO Zhengliang，HONG Xiang，WU Bing．Elasto －plastic earthquake response analysis of storey－post shear－ bending tall building structures［J］．Journal of Shenzhen University Science and Engineering，2004，21(2):116－122．

［9］包世华．新编高层建筑结构［M］．北京:中国水利水出版社，2001．BAO Shihua．Newly orgamzed tall building structures［M］．Beijing:China Waterpower Press，2001．

［10］夏桂云，欧见仁，李传习，等．考虑剪力墙剪切变形影响的框架－剪力墙结构分析［J］．工程力学，2013，30(6):217－222．XIA Guiyun，OU Jianren，LI Chuanxi，et al．Analysis method of frame－shear wall structures with considering shear deformation effect of shear wall［J］．Engineering Mechanics，2013，30(6):217 －222．

［11］Timoshenko S，Gere J．材料力学［M］．北京:科学出版社，1990．Timoshenko S，Gere J．Mechanics of material［M］．Beijing:Science Press，1990．

［12］肖明葵，刘纲，白绍良．滞回恢复力模型中求折点的一种方法［J］．重庆大学学报(自然科学版)，2002，25(1):13－16．XIAO Mingkui，LIU Gang，BAI Shaoliang．A method of computing rigidity turning point in hysteretic research force models［J］．Journal of Chongqing University(Natural Science Edition)，2002，25(1):13－16．

［13］中国建筑科学研究院建筑结构所．高层建筑结构设计［M］．北京:科学出版社，1983．Structural Institute of China Academy of Building Research．Design of Tall Building Structures［M］．Beijing:Science Press，1983．