深水域工程地质钻探套管选型与加固方案研究

王风华，刘晓明

(中铁大桥勘测设计院集团有限公司，武汉 430050)

岩土工程勘察中水域钻探施工较陆域困难许多，特别在水深且流速大的海域，起导向、隔水及护壁作用的套管下入海床前由于水流冲击变形，若其选型及加固方案选取不合理，套管将产生过大变形以致钻探无法进行［1］。

1 工程概况

拟建琼州海峡跨海大桥连接广东省徐闻县与海南省海口市，跨海部分长约26 km，桥址处最大海水流速4.8节(2.45 m/s)，最大海水深度108 m。针对琼州海峡水域流速大和深水问题，为保障海域勘探顺利进行，合理选择套管参数和加固方案十分必要。

2 套管绕流阻力计算公式及参数选取

套管置于匀速流动的海水中，一方面由于作用在迎流面前后管壁上的压强分布不对称，形成压强阻力;另一方面海水本身黏滞性切应力作用于管壁形成表面摩擦阻力。套管绕流阻力即为压强阻力和表面摩擦阻力之和，为套管对来流的反作用力，方向与海水流动方向相反［2］。

FD=0.5CDρV2A

式中，CD为绕流阻力系数;A为套管在垂直流体运动方向平面上的投影面积;ρ为海水密度;V为海水流动速度。

早在 1958 年，Hoerner［4］通过风洞试验对置于无限深的均匀来流的无限长直立圆柱、方柱、平板等的阻力进行测试，测得了不同障碍物下阻力系数CD与雷诺数Re的关系曲线。雷诺数(Re)是流体流动中惯性力与黏性力的比值，表达式如下

Re= ρVL/μ

式中，ρ为海水密度;V、L分别为流场的特征速度和特征长度;μ为流体动力黏度。

琼州海峡中部海水流速为0.5～4.8节(0.26～2.45 m/s)，平均海水温度为24℃，对应的动力黏度为1×10-3kg/m·s，特征长度L取套管直径0.18～0.30 m，海水密度取1.03 g/cm3，可得套管绕流对应的雷诺数Re为2.0×105～4.5×105，与之对应的阻力系数CD取1.2。

3 不同型号套管绕流阻力对比计算

水域钻探常用套管直径型号为φ127～φ299 mm，在深水及高流速区域则常用φ180 mm，壁厚5 mm。琼州海峡较浅水域，水深50 m左右钻探采用的方案就是φ180 mm套管加两道φ20 mm钢索保险绳，钢索分别固定于套管1/3，2/3处。这套方案实践证明是可行的，但当水深到80 m左右时这套方案在施工时则遇到了困难，那就是在水流冲击下套管变形过大，钻孔垂直度难以保证。

套管变形过大有3个方面的原因，一是套管本身轴惯性矩小了，刚度不够;二是水流冲击力太大;三是保险绳锚固位置不合理，没有充分发挥套管刚度。所以为了解决套管变形过大，就应增大套管刚度，减小迎流面积，合理布置保险绳锚固位置入手。

3.1 两锚固点套管系统变形特征

为了定量研究不同型号套管在不同流速下的变形特征，假设水深80 m，把两道保险绳固定于套管1/3、2/3处，海水流向平行于保险绳，变化套管型号和流速，利用ANSYS有限元软件计算分析套管的响应特征，套管采用pipe16单元，保险绳采用link单元，采用铰节点连接link和pipe单元，由于套管2/3以下为悬臂梁，故不同工况下变形量最大值均发生在套管最底部的节点上，位移特征见图1。

图1 海水冲击下套管及保险绳位移特征

3.2 不同流速下套管变形特征

选用φ273 mm×10 mm套管，计算流速1～5节时套管的最大变形量、最大弯矩以及钢索保险绳轴向力，结果见表1，图2。

表1 φ273 mm套管在不同海水流速下响应对比

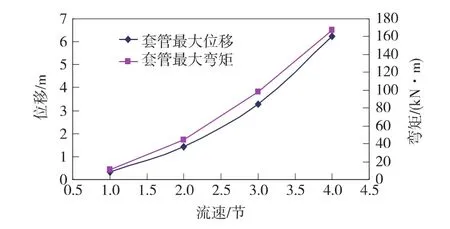
图2 套管位移和弯矩最大值与流速关系曲线

套管变形量、弯矩极值及保险绳拉力均与海水流速呈非线性增长关系，流速2.5节时是个转折点，此后曲线斜率增加更快，所以钻探下套管时应尽量在海水流速小于2.5节时施工，以减小套管变形量，保障下入海床后套管的垂直度。

3.3 不同套管直径下的变形特征

在海水流速为2节的情况下，选用不同直径的套管(壁厚均为10 mm)，对比分析不同直径下套管变形响应。计算结果见表2，图3。

表2 不同直径时套管响应对比

图3 套管位移和弯矩最大值与套管直径关系曲线

套管最大位移与其直径呈非线性关系，随套管直径增大最大位移不断减小，由图3可得在套管直径大于230 mm后最大位移减小幅度衰减，而最大弯矩与套管直径变化呈低斜率线性关系，对套管直径的变化不敏感。当套管直径超过230 mm后强调增大套管直径的方案并不能明显的减小套管变形量，这是因为此时套管的迎流面积也在增大，套管直径增大带来的刚度增大被同时增大的流水冲击力抵消严重，且大口径套管安装、拆卸都困难，故不应采用过大直径套管施工。

3.4 不同套管壁厚下的变形特征

在海水流速为2节的情况下，选用φ273 mm的套管，按照现有的标配壁厚尺寸，对比分析不同壁厚下套管变形响应。计算结果见表3，图4。

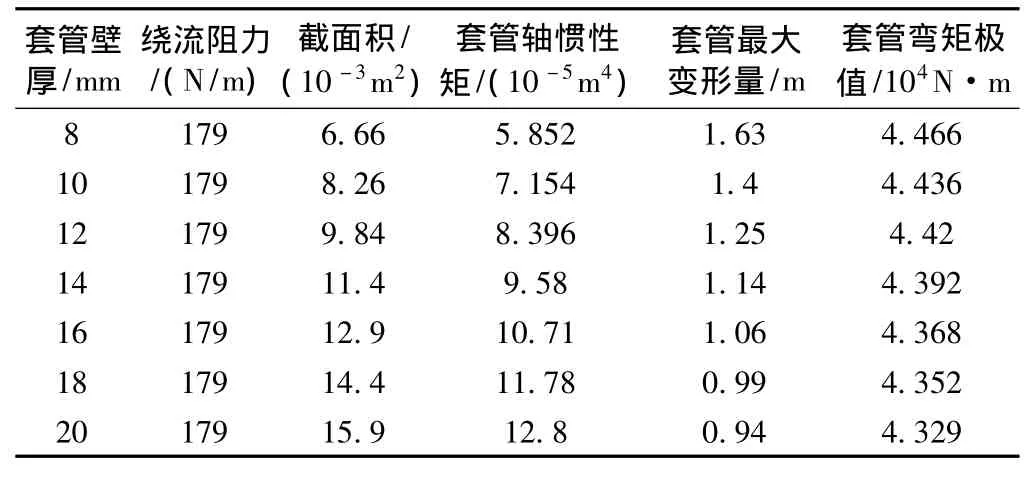
表3 不同壁厚时套管响应对比

套管最大位移、弯矩随套管壁厚增加呈非线性减小，且弯矩整体减小量不大，对壁厚的变化不敏感。最大位移在壁厚大于12 mm后对壁厚的变化敏感度也降低，故对于φ273 mm套管来讲12 mm壁厚较经济合理。

3.5 套管镂空后套管变形特征

为了减小流水对套管的冲击力，设计采用镂空套管导向定位后再下另外一层套管的施工方案，镂空减小了迎流面积，从而减小套管对海流的阻力，但减小套管截面积会使得套管轴惯性矩线性减小，套管刚度降低。对φ273套管在2节流速下，进行不同比例的镂空后其变形计算结果见表4，图5。

图4 套管位移和弯矩最大值与套管壁厚关系曲线

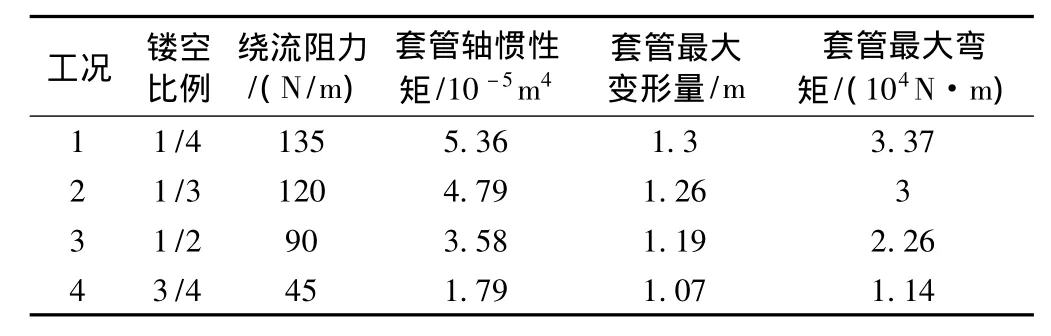
表4 对φ273 mm套管镂空不同比例下响应对比

图5 套管位移和弯矩最大值与镂空比例关系曲线

套管变形量及弯矩极值随镂空比例的增大而减小，但减小量并不大，从镂空1/4到3/4，变形量仅减小了0.23 m，最大弯矩降低幅度也有限;但镂空且另需一层套管的施工难度大、费用高，故这种方法是不可取的。

4 保险绳系于套管不同位置时套管变形响应

由于钻探施工船客观条件的限制，套管每侧只考虑两道保险绳，前面的计算分析均假设保险绳系于套管的1/3和2/3处，结果表明最大位移均发生在套管底端，极值弯矩最大值发生在靠下面的锚固点，最小值发生在第一个锚固点与套管顶端之间的中点，且方向与最大值相反。

为了减小套管的最大位移量，即底端节点的位移量，在套管型号、流速不变的情况下，应缩短下部悬臂梁的长度。对80 m长套管的第二个锚固点变化位置，第一个位置则平分套管顶端与第二个锚固点，计算结果见表5，图6。

表5 保险绳系于φ273 mm套管不同位置时套管响应对比

图6 套管位移和弯矩最大值与保险绳锚固位置关系曲线

随着第二个锚固点的下移，套管的最大位移及弯矩均近线性减小，但当第二锚固点位置大于84%时，最大位移出现拐点，呈上升趋势，此时，最大位移点不是底部端点，而是2个锚固点的中间位置。故2个锚固点的最佳位置约为42%和84%。

5 结语

对比分析套管位移和弯矩对不同流速、套管直径、套管厚度、镂空度以及锚固位置工况的响应，可以得到以下几点结论:

(1)不同工况下套管最大位移点均为底部端点;

(2)水深80 m时，钻探下套管时应尽量在海水流速小于2.5节时施工;

(3)套管直径增大对刚度的贡献被随之增加迎水面积所抵消，套管位移对直径变化不敏感;

(4)套管最大位移、弯矩随套管壁厚增加呈非线性减小，对于φ273 mm套管壁厚12 mm较经济合理;

(5)镂空套管以减小迎水面积的方案不可取;

(6)套管采用2个锚固点时，锚固点最佳位置约为42%和84%。

琼州海峡跨海大桥工程地质钻探施工实践证明，科学合理的套管保护系统为勘察外业的顺利进行提供了重要保证。

［1］ 邓绍云.桩基绕流阻力特性研究现状与展望［J］.水运工程，2006.

［2］ 王光辉，陈必超.浅海水域工程勘察钻探方法和技术措施［J］.探矿工程，2003.

［3］ 周云龙，郭婷婷.高等流体力学［M］.北京:中国电力出版社，2008.

［4］ Honemer S F.Fluid Dynamic Dray［M］.［S.I.］Honemer Fluid Dynamics，1958.