扁板侧胀试验获取温州软黏土不排水抗剪强度试验研究
2014-01-03涂启柱
涂启柱
(中铁第四勘察设计院集团有限公司,武汉 430063)
扁板侧胀试验(简称DMT试验),是由意大利Silvano Marchetti于1980年创立[1],最早在北美和欧洲使用,随后迅速推广,并先后列入ASTM(1986)推荐方法和欧洲Eurocode 7(1997)规范,我国在20世纪90年代开始引进和使用这项技术。目前DMT试验方法及其应用已经得到了多国的认可,被认为是一种操作简单、重复性好、人为影响小、且较经济的原位测试方法[2],已列入我国国家标准《岩土工程勘察规范》[3],并已纳入我国铁路行业标准《铁路工程地质原位测试规程》[4]。
不排水抗剪强度是软黏土重要的力学特性参数,对土体的强度特性分析和稳定性评价具有重要影响。最近30年,国外学者对利用扁板侧胀试验获取软黏土不排水抗剪强度参数有了一定的试验研究,国内学者主要针对上海地区进行了一些研究,但由于土体沉积时的环境、气候、物质等的差异,各地的土性不尽相同,而且国内外试验仪器性能、试验标准也不尽相同,因此在利用扁板侧胀试验确定土性指标时,必须重视各地的地区经验[3]。
针对温州海相沉积软黏土进行了多种原位测试试验,并利用多元回归分析方法,探求温州软黏土地区扁板侧胀试验参数与不排水抗剪强度参数之间的相关关系。
1 扁板侧胀试验获取不排水抗剪强度研究现状
扁板侧胀试验是利用外力将一扁平状测头压入地基土达某一深度后加气压使测头一面的膜片向外膨胀,测得在特定位置时膜片所受的相应气压值A、B和C,从而获得土体受力与变形关系的一种原位测试方法[1]。
根据试验前率定获得的膜片约束力A、B及试验时测得的气压值A、B、C利用土体弹性性质可得出膜片在不同位置时的土压力[4]。

式中,Zm为未调零时压力表初读数,kPa;P0为膜片向土中膨胀之前作用在膜片上的接触压力,kPa;P1为膜片膨胀1.10 mm时膨胀压力,kPa;P2为膜片回到0.05 mm时受到的终止压力,kPa。
根据以上土压力值和各试验点静止水压力u0及上覆有效土压力值可以获得以下参数。
划分地基土层的材料指数为

反映地基土固结历史的水平应力指数为

反映地基土力学性质的侧胀模量为
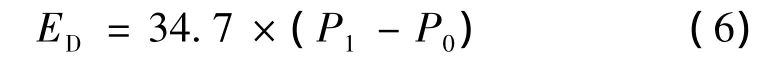
反映地基土孔压特性的孔压指数为

Marchetti(1980)[1]最早提出利用扁板侧胀试验计算地基土的不排水抗剪强度Cu
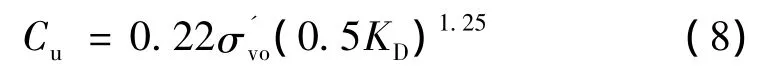
之后国外其他学者,Mayne(1987)、Lacasse和Lunne(1988)、Roque(1988)以及 Iwasaki和 Kamei(1995)等[5]根据各自不同地区的试验资料对式(8)作出了修正(表1)。
国内在这方面的研究主要集中在上海地区,陈国民(1999)[6]针对上海浅层黏土,根据土性指数ID的不同,对式(8)进行了修正,当ID≤0.35时,可根据式(8)计算,当ID>0.35时,根据下式计算
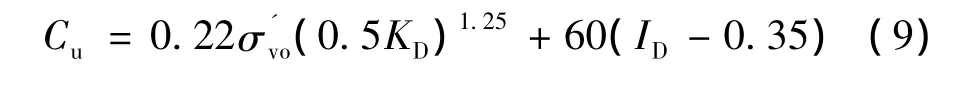
孙莉等(2002)[7]针对于上海地区的软土层,建立了扁板模量ED与不排水抗剪强度cu具有线性相关性,其关系式为
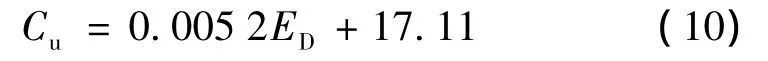
国内外学者利用扁板侧账试验获取黏土不排水抗剪强度的研究成果汇总如表1所示。

表1 用DMT计算不排水抗剪强度公式汇总
2 多元回归分析方法
由于岩土工程中室内、室外试验机理及边界条件的复杂性,直接从理论上推导出两种试验各参数间的函数关系往往是比较困难的。因此,为研究两种试验的关系,可借助数理统计的方法,建立试验参数间的相关关系,这在工程中是可行的。为提高回归分析的精度,一般可采用多元回归分析的方法。
2.1 选元分析
在多元回归分析中,自变量的选择是很重要的。如果遗漏了重要的变量,回归分析的效果一定不会好;如果变量过多,将会把对应变量y影响不显著的变量也选入回归方程,这样就影响了回归方程的稳定性,效果也好不了。因此在研究因变量与自变量之间回归关系时,需要从众多自变量中筛选出比较重要的若干个自变量来建立回归方程,这个过程即为选元分析[9]。通过选元分析可以减轻回归分析中的计算工作量,更重要的是能增加回归方程的使用价值。选元分析一般可分为:前进法、后退法、最优子集法、逐步回归法。其中逐步回归法结合了前进法与后退法的优点,该法考虑了在向前挑选自变量过程的同时还提出新发现的次要变量。
2.2 回归分析

3 扁板侧胀试验确定不排水抗剪强度试验研究
3.1 试验场地概述
温州市域铁路拟建工程经过区域多属于冲海积平原区,为一套自中更新统到全新统的海相、陆相及海陆过渡相的松散层。沿铁路线选择4个试验场地各布置1个钻探孔、1个扁板侧胀试验孔、2个静力触探试验孔(分为单桥与双桥静力触探试验)与1个十字板剪切试验孔。试验场地地层分为①耕植土;②-1淤泥,②-2淤泥质粉质黏土;③细砂;④-1粉质黏土,④-2黏土等(图1、图2)。由现场试验及室内试验可以探明试验场地普遍存在淤泥、淤泥质黏性土等软土,呈厚层状大面积分布,含水量高、压缩性大、强度低、天然孔隙比大等特征(表2)。
3.2 选元分析
P0、P1与P2是扁板侧胀试验数据经修正后直接得到的参数,最能直接反应土的物理力学特性。通过对 Marchetti(1980)[1]等国外学者及陈国民(1999)[5]等国内学者的研究成果分析可以得出不排水抗剪强度Cu与(P0-u0)有密切的关系,国内学者孙莉等(2002)[6]的研究成果也说明不排水抗剪强度Cu与P1有一定的关系,为了兼顾分析的全面性与提高分析的精度,将P0-u0、P1-u0及P2-u0作为自变量纳入回归分析。
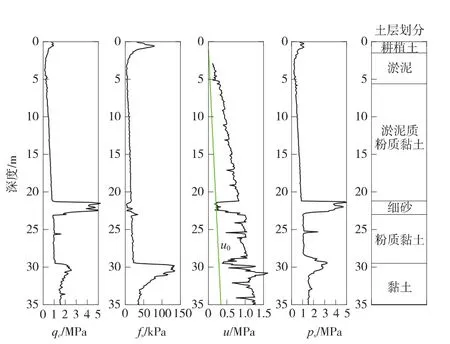
图1 温州市域铁路试验场地静力触探曲线

图2 温州市域铁路试验场地DMT侧胀试验曲线

表2 温州市域铁路试验场地软黏土的主要物理力学性质指标
3.3 回归分析
目前测试黏性土不排水抗剪强度的最直接的方法是十字板剪切试验(VST)。因此,回归分析的应变量取十字板剪切试验得出的不排水抗剪强度。取显著性水平α=0.05,按逐步回归分析法对其作回归分析。变量的检验结果见表3与表4。
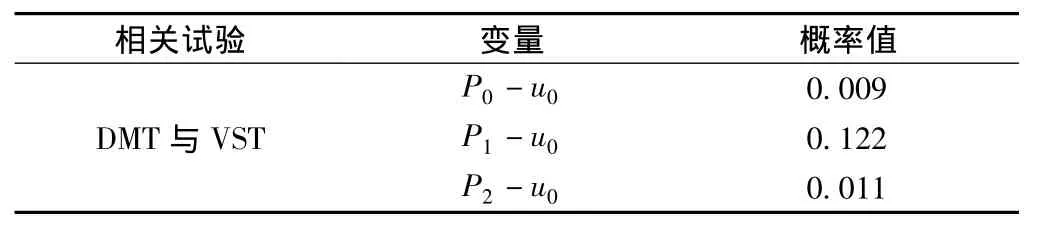
表3 各变量的检验结果
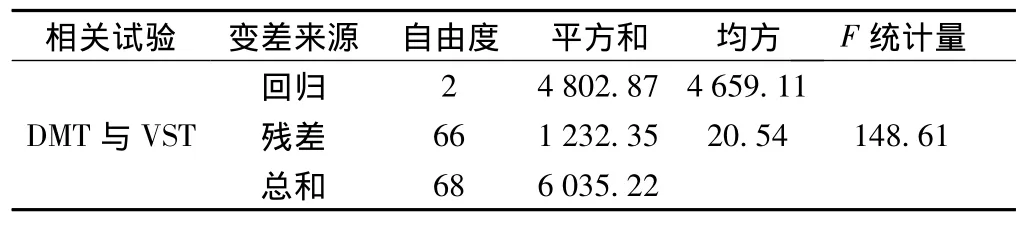
表4 方差分析
从表3可以看出P0-u0与P2-u0两个变量的概率值均小于0.05,即两变量通过检验,而P1-u0变量的概率值大于0.05,即该变量没通过检验,说明P0-u0与P2-u0两个变量对不排水抗剪强度的影响是显著的,而P1-u0变量对不排水抗剪强度的影响不显著。经多元回归分析后,得
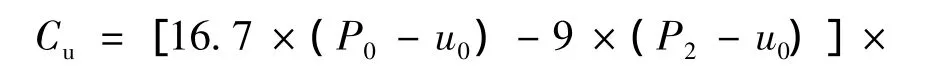
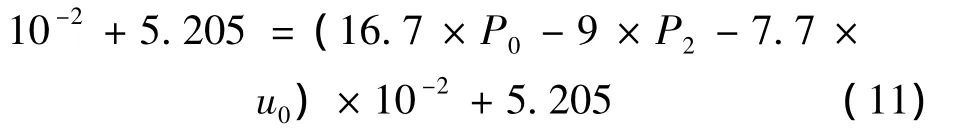
式中各参数的单位均为kPa。式(11)的相关系数R2=82.6,统计量 F 值:F=148.61>F0.05(2,66)=3.14,说明线性回归作用是显著的,回归Cu值与实测值的关系见图3。

图3 C u实测值与回归值之间的关系
4 结语
扁板侧胀试验操作简单、重复性好、人为影响小,扁板侧胀试验得到的参数与土体不排水抗剪强度参数具有较好的相关性,但这种相关性对不同地区、不同成因的土体存在一定的差异性。
多元回归分析方法是一种有效的数理统计手段,通过多元回归与选元分析,可将诸多因素中影响权重较大的因素选出无关因素删除,使得到的回归方程更为合理。本文利用多元回归分析方法,对温州地区多个试验点的试验数据进行分析,建立了扁板侧胀试验参数与十字板试验不排水抗剪强度参数之间的经验关系。
本文所建立的经验公式适用于温州海相沉积软黏土地区地基土埋深小于30 m的土性条件,在其他地区使用还有待验证。
[1] Marchetti S.In-situ tests by flat dilatometer[J].Journal of Geotechnical Engineering,ASCE,1980,107(3):832-837.
[2] 储团结,王中华,黄俊杰.扁板侧胀试验在高速铁路软土地基勘察中的应用研究[J].铁道勘察,2005(5):49-52.
[3] 中华人民共和国住房和城乡建设部.GB50021—2001 岩土工程勘察规范[S].北京:中国建筑工业出版社,2009.
[4] TBl0018—2003 铁路工程地质原位测试规程[S].北京:中国铁道出版社,2003.
[5] Marchetti S.The flat dilatomter:design applications[C].Third geotechnical engineering conference,Cairo university,1997.
[6] 陈国民.扁板侧胀试验及其应用[J].岩土工程学报,1999,21(2):117-183.
[7] 孙莉,孙仕林.用扁板侧胀试验计算饱和软黏土的不排水抗剪强度[J].岩土工程技术,2002(6).
[8] Lutenegger A J.Current status of the Marchetti dilatometer test[A].Proceedings of the first International Symposium on Penetration Testing[C].Orlando:[s.n.],1988(1):137-155.
[9] 王黎明,等.应用回归分析[M].上海:复旦大学出版社,2008.
