基于通道选择技术的统计MIMO雷达CFAR检测器

杨 俭，曲长文，周 强

(海军航空工程学院电子信息工程系， 山东烟台264001)

0 引言

当各个观测通道输出的局部检测统计量在统计意义上都相同时，统计多输入多输出(MIMO)雷达目标检测问题对应的检测统计量，在形式上一般都可归结为对所有观测通道输出的局部检测统计量直接进行非相参积累，从而获得近似恒定的输出信噪比，以此缓解目标角闪烁给检测性能造成的影响，达到改善检测性能的目的。

在均匀背景和各个观测通道目标回波统计独立的假设条件下，大量文献研究了高斯白噪声或高斯/复合高斯杂波背景中的统计MIMO雷达目标检测问题，所提出的检测统计量基本都是对所有观测通道输出的局部检测统计量进行非相参积累的形式。其中，对于高斯白噪声背景来说，每个通道输出的局部检测统计量通常是该通道对应的匹配滤波器的输出［1-4］或其归一化形式［1］，而对于高斯/复合高斯杂波背景来说，其局部检测统计量通常包含白化处理和匹配滤波等过程［5］，或者直接采用自适应匹配滤波器［6］、自适应子空间检测器［6］等一些已知的检测器形式。在非均匀高斯杂波背景中，文献［7-9］研究了统计MIMO雷达CA-CFAR、OSCA-CFAR和 LCIOSCA-CFAR三种检测器，其中，检测统计量的形式均是所有观测通道的平方律检波输出之和，而CA、OSCA和LCIOSCA均是指杂波功率水平的估计方法。

然而，事实上并不能保证各个观测通道输出的局部检测统计量在统计意义上都是相同的。特别是在杂波背景条件下，不同观测通道中的目标谱与杂波谱的相对位置通常不同，这就导致各个局部检测统计量可能具有不同的输出信噪比，也就是说，这些局部检测统计量不是统计相同的。显然，就前面总结的对各个局部检测统计量直接进行非相参积累的检测结构而言，那些具有非常低输出信噪比的局部检测统计量将会恶化基于这种检测结构的检测器的性能。本文将具有非常低输出信噪比的观测通道定义为无效通道，反之则定义为有效通道。

对于基于各个局部检测统计量直接非相参积累的统计MIMO雷达检测器来说，当存在无效观测通道时，若能在非相参积累之前剔除掉这些无效通道，则必将明显改善检测性能。然而，如何区分无效通道与有效通道，即如何执行所谓的通道选择，成为了一个急需解决的问题。文献［10］利用各观测通道输出局部检测统计量之间的相关矩阵的特征分解，提出了主分量检测方法，只对那些具有较大特征值的有效通道进行非相参积累。不过这种方法需要估计通道间的相关矩阵，而且主分量方法通常需要较高的信噪比才能准确地分离有效通道与无效通道。

本文采用顺序统计量理论来解决通道选择问题。在推导统计MIMO雷达各观测通道中检验单元背景与参考单元背景功率水平不同条件下GLRT检测器的基础上，提出了基于顺序统计量(OS)理论的通道选择技术及其相应的OS-GLRT检测器和改进的OS-GLRT检测器(Modified OS-GLRT，MOS-GLRT)检测算法。最后给出仿真分析与总结。

1 问题的形成与检测器设计

1.1 问题的描述与GLRT检测器的推导

假设统计MIMO雷达系统由M个独立观测通道组成。第i(i=1，2，…，M)个观测通道收集的来自K+1 个距离单元的观测矢量集合记为 Xi={xi，zi，1，zi，2，…，zi，K}，其中，各观测矢量相互统计独立。xi=si+zi，0=αihi+zi，0表示来自当前检验单元的观测矢量，si是目标观测矢量，hi是L维已知的目标导向矢量，αi是描述目标起伏和通道效应的零均值复高斯随机变量，zi，0是零均值、协方差矩阵为Ri的复高斯随机矢量。zi，1，zi，2，…，zi，K表示来自 K 个参考距离单元的观测矢量，且都是零均值、协方差矩阵为Ri的复高斯随机矢量，这意味着各观测通道中检验单元与参考距离单元的背景功率水平不同。采用文献［11］提出的统计MIMO雷达经典线性模型，本文的检测问题可描述为如下二元假设检验

式中:α=［α1，α2…，αM］T，H=diag(h1，h2，…hM)。假设各个通道收集的观测矢量集合Xi(i=1，2，…，M)相互统计独立，那么根据奈曼-皮尔逊准则，上式所示的二元假设检验问题的最优解是式(2)所示的似然比检验

式中:fi(Xi|H0)和fi(Xi|H1)分别表示H0和H1假设条件下，第i个通道的观测矢量集合Xi的联合概率密度函数

式(2)和式(3)中，σi，αi，Ri等参量都是未知的，需替换为相应的最大似然估计。由于各个通道的观测矢量集合之间相互统计独立，因此第i个通道中未知参量的估计与其他通道无关。于是对于每个观测通道来说，可直接采用文献［12］的结果。将各个通道的推导结果代入式(2)中，并经过化简变形即可得到如下的GLRT统计量

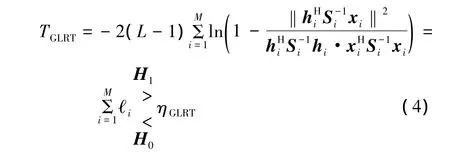
式中:ℓi表示第i个观测通道输出的局部检测统计量，且各个ℓi(i=1，2，…，M)之间相互统计独立。根据文献［13］的统计等价分解结果推导可得，在H0假设条件下，ℓi的概率分布只与K和L有关，因此，任何基于ℓi构造的检测器都将具有CFAR性质。

式(4)给出的GLRT统计量就是对各个观测通道输出的局部检测统计量ℓi直接求和。从多通道信息融合［14］的角度来说，此GLRT统计量只是其中的一种融合方式，适用于所有观测通道的输出局部检测统计量ℓi统计相同的情况。但是，正如前面所述，实际中各个观测通道输出的局部检测统计量并不一定统计相同，可能存在无效通道，从而降低了GLRT统计量的检测性能。在1.2节中，本文将提出基于顺序统计量理论的通道选择技术，用来剔除无效通道，挑选具有较高输出信噪比的局部检测统计量进行非相参积累，并以此为基础构建新的检测器。

1.2 基于顺序统计量通道选择技术的OS-GLRT检测器

当各个观测通道的输出信噪比存在较大差异时，可以考虑只非相参积累那些具有较大输出信噪比的观测通道。假设实际的有效通道数量为m0，而事先估计或先验已知的有效通道数量为me，那么一种合理的多通道信息融合方式是对各个观测通道的输出局部检测统计量ℓi排序，然后取me个最大的ℓi值进行非相参积累，从而得到基于OS通道选择技术的CFAR检测器——OS-GLRT检测器。

将各个观测通道输出的局部检测统计量ℓi，i=1，2，…，M，按升序排列

那么OS-GLRT检测器可表示为

下面对OS-GLRT检测器作一些评论:

(1)当存在无效通道时，不像GLRT检测器，OSGLRT检测器能够通过剔除那些无效通道而减小性能损失;

(2)从OS-GLRT检测器的检测结构来看，me将会显著影响OS-GLRT检测器的检测性能，原因在于它较大程度地决定了最终的检测门限。上述两条评论将会在后续的检测性能评估中得到证实;

(3)由于观测环境的不确定性，me通常不总是等于m0。

本文中，为了表述方便，将m0=me的情况称为“匹配情况”，而将m0≠me的情况称为“失配情况”。显然，当me=M时，OS-GLRT检测器就变成了GLRT检测器;而当me=1时，OS-GLRT检测器就变成了最大值检测器。

2 GLRT和OS-GLRT检测器的虚警概率

由于将要推导的是虚警概率PFA表达式，所以本节的概率密度函数均是指H0假设下的概率密度函数。

求解GLRT检测器和OS-GLRT检测器的虚警概率表达式必须先求解ℓi的概率密度函数。然而根据文献［13］，ℓi的概率密度函数具有很复杂的形式，因此在此基础上很难求得上述两个检测器的虚警概率表达式。但是当各个观测通道中包含的参考距离单元数量 K→∞时，意味着 Si→Ri，此时根据文献［13］，ℓi的概率密度函数具有很简洁的指数分布形式，fℓi(x)=e-x/2/2，这给求解GLRT检测器和OS-GLRT检测器的虚警概率表达式提供了便利。为了简单起见，仍用第1节中的符号来表示K→∞时各观测通道输出的局部检测统计量。

在H0假设条件下，各个ℓi相互统计独立，且都服从上述指数分布，因此式(4)的TGLRT服从自由度为2M的中心卡方分布，其虚警概率为PFA，GLRT(ηGLRT)=Γ(M，ηGLRT/2)/Γ(M)，其中，Γ(·)表示伽马函数，ηGLRT是GLRT检测器的CFAR门限。

根据顺序统计量理论，式(5)中各局部检测统计量ℓ(i)(i=1，2，…，M)的联合概率密度函数如文献［15］所示，下面重写为

式中:后一个等式将难于计算的me重积分转化为一个便于计算的me次积分。最后得到了OS-GLRT检测器的虚警概率表达式

式中:ηOS-GLRT是对应于me个最大的局部检测统计量求和的OS-GLRT检测器的CFAR门限。以M=9，me=3为例，经过简单的指数函数的积分运算，即得PFA，OS-GLRT(ηOS-GLRT)关于 ηOS-GLRT的显式表达式

3 基于顺序统计量通道选择技术的MOSGLRT检测算法

OS-GLRT检测器需要事先估计有效通道的数量，且在“失配情况”中，OS-GLRT检测器的性能将会有所恶化，然而，不幸的是，“失配情况”在实际中是不可避免的，而且是经常会发生的。因此，必须开发一种对有效通道数量估计不敏感或者不需要估计有效通道数量的通道选择技术。为此，本节在OS-GLRT检测器的基础上进行了修正，提出了一种修正的OS-GLRT检测算法，即MOS-GLRT检测算法。MOS-GLRT检测算法的执行步骤如下:

步骤1:对M个局部检测统计量ℓi进行升序排列，并将后k个最大的局部检测统计量值之和记为Tk(k=1，2，…，M)，且将对应于 Tk的 CFAR 门限记为ηk。

步骤2:规定无目标条件下Tk超过ηk的概率都相同，记为PFA0。利用式(10)可由PFA0求得各个Tk对应的CFAR门限ηk。

步骤3:比较 Tk与 ηk(k=1，2，…，M)，只要有一个k使得Tk≥ηk成立，则判决为有目标，否则判决为没有目标。

关于MOS-GLRT检测算法的上述步骤作如下两点说明:

(1)由步骤1可知，MOS-GLRT检测算法实际上需要计算M种有效通道数量条件下的OS-GLRT统计量，同时利用式(10)计算PFA0以及M种有效通道数量条件下OS-GLRT统计量对应的M个CFAR门限。不过也正因为如此，MOS-GLRT检测算法不需要事先估计有效通道的数量;

(2)由步骤3可知，步骤2中的虚警概率PFA0并非MOS-GLRT检测算法最终所需要的虚警概率PFA，且显然有PFA＞PFA0。但由于难以确定各个Tk之间的相关性，因此，由设定的虚警概率PFA求得PFA0的过程是通过Monte-Carlo仿真来实现的。

4 仿真与分析

本节将利用ℓi的统计等价分解表达式对OS-GLRT检测器和MOS-GLRT检测算法的检测性能进行评估。ℓi的统计等价分解表达式如下所示［13］

式中:hi，0，hi，1，hi，2，hi，3，hi，4都是相互统计独立的，hi，1，hi，2，hi，3的平方分别服从自由度为 K-L+1，K-L+2，L-1的中心复卡方分布;hi，4服从零均值单位方差的复高斯分布;在H0假设条件下，hi，0也服从零均值单位方差的复高斯分布，而在H1假设条件下，其均值的模平方表征的是第i个观测通道的输出信噪比。

表1给出了仿真中采用的各观测通道输出信噪比的3种模型，其中，ε表示所有观测通道中的输出信噪比之和。模型1中，各个观测通道的输出信噪比都是相同的，即ε/M，故模型1表示均匀分布模型;相反，模型2和模型3表示了非均匀分布模型，模型2中90%的能量分布在前m0个观测通道中，而模型3中100%的能量分布在前m0个观测通道中。

表1 输出信噪比在各个通道之间的分布模型

4.1 GLRT、OS-GLRT以及MOS-GLRT的检测性能比较

本节将比较分析不同的输出信噪比分布模型情况下，GLRT、OS-GLRT检测器以及MOS-GLRT检测算法的性能，其中，对于OS-GLRT检测器来说，考虑的是“匹配情况”，即模型1中，me=M，而模型2和模型3中，me=m0。

图1给出了表1中3种输出信噪比分布模型条件下这3个检测器的检测概率PD与ε的关系曲线，其中，对于模型1来说，由于me=M，故此时的GLRT检测器与OS-GLRT检测器的性能曲线是重合的;对于MOS-GLRT检测算法来说，根据图注中所给定的参数，通过Monte-Carlo仿真可得，为达到PFA=10-4而所要求的 PFA0为3.83×10-5。

图1 不同分布模型中3个检测器的性能比较，M=9，L=4，K=8，PFA=10-4，模型1:m0=9，模型2 和模型 3:m0=3

由图1可以得出如下一些结论:

(1)3个检测方法在模型1中性能最好，而在模型3中性能最差。这是一个显而易见的结果。观测通道间的非均匀性必然会导致性能损失，非均匀程度越高，性能损失就越大;而且这种非均匀性对没有通道选择技术的GLRT检测器的影响最大，对OSGLRT检测器次之，而对MOS-GLRT检测算法的影响较前二者小;

(2)与GLRT检测器和OS-GLRT检测器相比，MOS-GLRT检测算法的性能在3种分布模型条件下都接近于前二者中的优胜者，而明显优于前二者中的较差者。具体而言，在模型1和模型2中，MOS-GLRT检测算法的性能接近于GLRT检测器，而在模型3中，其性能接近于OS-GLRT检测器。这意味着在输出信噪比的这3种分布模型中，MOS-GLRT检测算法比另外两个检测器更稳健;

(3)在模型3中，OS-GLRT检测器优于GLRT检测器，而在模型1和2中，则比GLRT检测器差，这意味着OS-GLRT检测器只有在各观测通道输出信噪比差异很显著时才能改善GLRT的检测性能。

4.2 OS-GLRT检测器的性能分析

不失一般性，本节只讨论模型3情况中OS-GLRT检测器的检测性能。图2给出了“失配情况”下OSGLRT检测器的PD与ε的关系曲线，其中，me分别取1，3，4，6 和9，且me=1 表示最大值检测器，me=3 表示匹配情况，me=9表示GLRT检测器。

图2 不同me条件下，OS-GLRT检测器的检测性能曲线，M=9，m0=3，L=4，K=8，PFA=10-4

由图2可知，当me=3和4时，OS-GLRT检测器具有最佳的性能，而对于me的其他值，其检测性能有不同程度的下降，而且失配越严重，遭受的性能损失越大。对比me＜m0和me＞m0这两种情况可以发现，me＜m0时导致的性能损失大于me＞m0的情况，这是因为低估有效通道的数量会较大程度地损失目标能量。

由式(6)可知，匹配情况下，随着m0逐渐增加至M，OS-LRT检测器逐渐变成了GLRT检测器。更准确地说，对于模型3，GLRT检测器的性能随着m0的增加逐渐接近OS-GLRT检测器的性能。因此，有必要考察m0增大到何种程度时OS-GLRT检测器相对于GLRT检测器的优势可以忽略，这样就可以避免此时采用OS-GLRT检测器带来的额外的运算复杂度，将此时的m0记为 m0。

图3给出了匹配情况下m0取不同值时，OS-GLRT检测器与GLRT检测器的PD与ε关系曲线。图中表明，当 m0≥=6时，OS-GLRT检测器相对于GLRT检测器的优势已经小到可以忽略了。当然，对于不同的M，L，K 值值是不同的。

图3 不同m0条件下，OS-GLRT与GLRT的性能比较，M=9，me=m0，L=4，K=8，PFA=10-4

根据4.1节和4.2节的分析，可对OS-GLRT检测器作如下总结:

(1)只有当各观测通道中输出信噪比的差异非常显著时，例如模型3，OS-GLRT检测器的性能才优于GLRT检测器;

(2)OS-GLRT检测器的性能对me很敏感，尤其是当 me＜m0时;

(3)在匹配情况中，当m0超过某个值时，为了那么一点点可忽略不计的性能增益而采用OS-GLRT检测器并不值得，因为OS-GLRT检测器的排序操作会带来额外的运算复杂度。

4.3 MOS-GLRT检测算法的性能分析

由图1可知，对于“匹配情况”，OS-GLRT检测器的检测性能在第2种输出信噪比分布模型条件下不如MOS-GLRT检测算法，原因在于第2种模型不像第1种和第3种那样将全部能量均匀地分布在m0个观测通道中，而是只有大部分能量分布在这m0个观测通道中。在第2种输出信噪比分布模型下，GLRT检测器的检测性能是三者中最好的，但MOS-GLRT检测算法的性能与之很接近。

本节主要是针对“失配情况”，比较3种输出信噪比分布模型条件下，OS-GLRT检测器与MOS-GLRT检测算法的性能，性能曲线如图4所示。由图可知，对于输出信噪比的3种分布模型中的任何一种分布模型，OS-GLRT检测器的性能受预先估计的有效通道数量me的影响很大，me的最差估计与最优估计导致的OSGLRT检测性能之间的差异都在5 dB以上。然而在这3种分布模型中，不需要事先估计有效通道数量的MOS-GLRT检测算法的性能都接近于me最优估计时的OS-GLRT检测器的性能，这体现了MOS-GLRT检测算法相对于OS-GLRT检测器的明显优势。

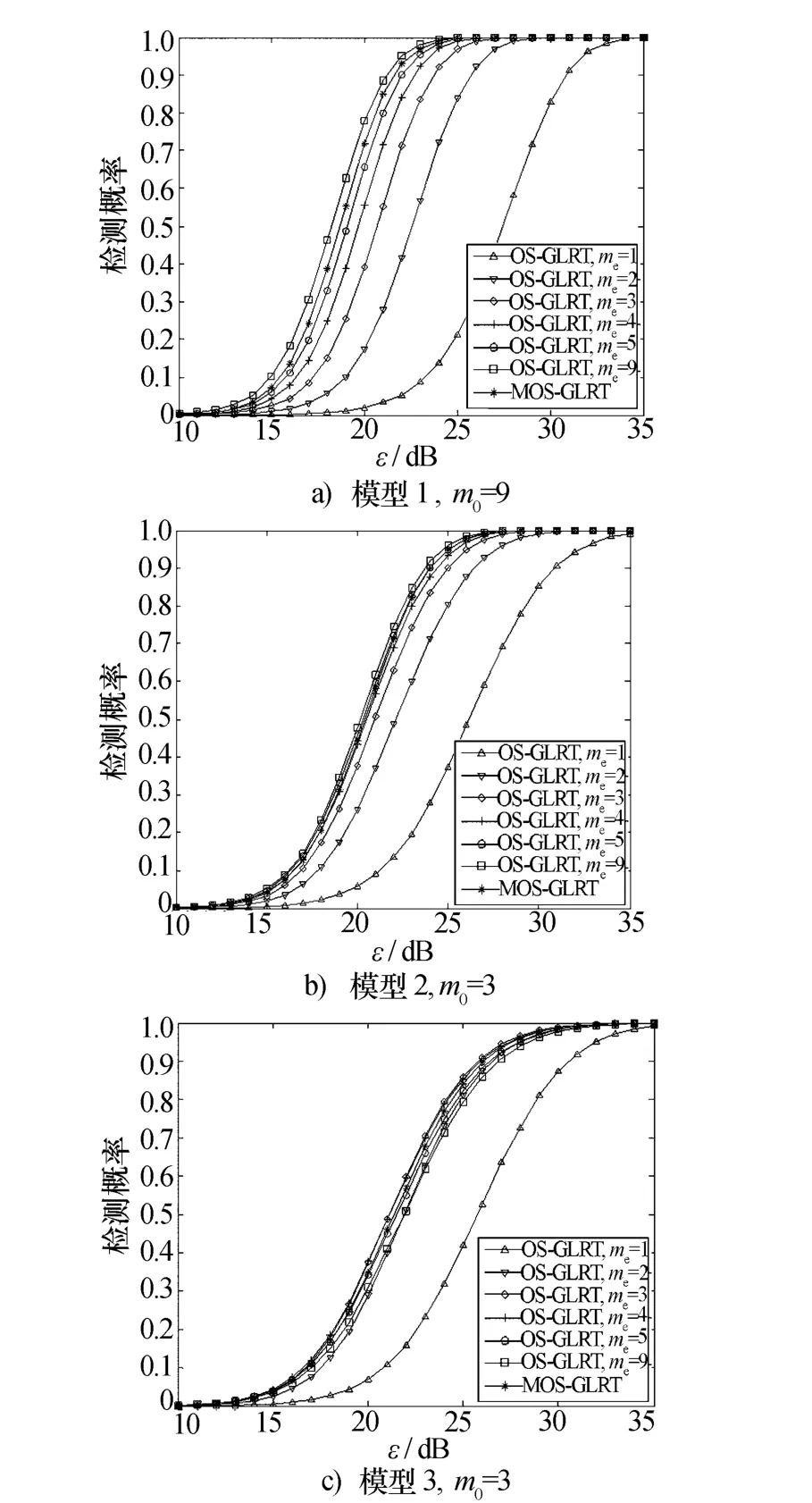
图4 3种分布模型和不同me条件下，OS-GLRT检测器与MOS-GLRT 检测算法的性能比较，M=9，L=4，K=8，PFA=10-4

5 结束语

本文研究了高斯背景中统计MIMO雷达的目标检测问题，提出并分析了两种基于顺序统计量通道选择技术的CFAR检测方法，即OS-GLRT检测器和MOSGLRT检测算法。

OS-GLRT检测器是在事先估计或先验已知有效通道数量me的前提下，非相参积累me个最大的局部检测统计量形成最终的检测统计量。OS-GLRT检测器的检测性能在各观测通道输出信噪比差异非常显著时优于传统的GLRT检测器。然而，当考虑到实际应用时，OS-GLRT检测器存在着一些不尽如人意的地方，例如，当各观测通道输出信噪比差异不那么显著时，OS-GLRT检测器相对于传统的GLRT检测器并没有检测性能上的明显优势。而且，OS-GLRT检测器对预先估计的有效通道数量比较敏感，特别是当低估有效通道数量时，OSGLRT检测器的性能将会显著下降。

为了克服OS-GLRT检测器的上述缺陷，本文在OS-GLRT检测器的基础上提出了一种修正算法，所得到的MOS-CFAR检测算法实际上是采用“或规则”，对各种有效通道数量假设下得到的OS-GLRT检测器与相应的CFAR门限的比较结果进行融合，只有当所有的比较结果都判决为没有目标时，MOS-GLRT检测算法才判决为没有目标。显然这种做法会增加虚警概率，而维持原先设定的虚警概率的方法是，降低各种有效通道数量假设下OS-GLRT检测器与相应CFAR门限进行比较时的虚警概率。

第4节的仿真表明，当各个观测通道的局部检测统计量的输出信噪比差异越大时，OS-GLRT检测器的优势越明显，当然这是建立在正确估计有效通道数量的基础之上的;反之，当各局部检测统计量的输出信噪比的差异越小时，GLRT检测器的优势越明显。而MOS-GLRT检测算法的性能在这两种情形下都接近于GLRT检测器和OS-GLRT检测器中的优胜者，而明显优于这二者中的较差者，并较好地克服了OS-GLRT检测器对有效通道数量估计值比较敏感的问题;而且，由于MOS-GLRT检测算法无需事先估计有效通道的数量，因此便于实际操作。不过目前存在的问题是，难于求解各种有效通道数量假设下得到的各种OS-GLRT统计量之间的相关性，因而难以推导MOS-GLRT检测算法的虚警概率表达式。另外，本文主要讨论的是统计独立观测通道的情况，后续还需要进一步地研究与分析完全相关观测通道和部分相关观测通道条件下的通道选择技术及其相应的CFAR检测器。

［1］ Fishler E，Haimmovich A，Blum R S，et al.Spatial diversity in radar-models and detection performance［J］.IEEE Transactions on Signal Processing，2006，54(3):823-838.

［2］ Tang Jun，Wu Yong，Peng Yingning.Diversity order and detection performance of MIMO radar:a relative entropy based study［C］//2008 IEEE Radar Conference.Rome:IEEE Press，2008:1-5.

［3］ 曾建奎，何子述.慢起伏目标的多输入多输出雷达检测性能分析［J］.电波科学学报，2008，23(1):158-161.Zeng Jiankui，He Zishu.Analysis of MIMO detection performance for slow fluctuating target［J］.Chinese Journal of Radio Science，2008，23(1):158-161.

［4］ 王敦勇，马晓岩，袁俊泉，等.MIMO雷达与相控阵雷达的多脉冲检测性能比较［J］.雷达科学与技术，2007，5(6):405-409.Wang Dunyong，Ma Xiaoyan，Yuan Junquan，et al.Detection performance comparison between MIMO radar and phased array radar based on multiple pulses［J］.Radar Science and Technology，2007，5(6):405-409.

［5］ Sammartino P F，Baker C J，Griffiths H D.MIMO radar performance in clutter environment［C］//2006 CIE International Conference on Radar.Shanghai:IEEE Press，2006:32-35.

［6］ Sheikhi A，Zamani A.Temporal coherent adaptive target detection for multi-input multi-output radars in clutter［J］.IET Radar，Sonar and Navigation，2008，2(2):86-96.

［7］ 王敦勇，马晓岩，袁俊泉，等.MIMO雷达中单元平均恒虚警检测性能分析［J］.电子对抗，2008(1):34-38.Wang Dunyong，Ma Xiaoyan，Yuan Junquan，et al.Detection performance analysis on CA-CFAR in MIMO radar［J］.Electronic Warfare，2008(1):34-38.

［8］ 王敦勇，马晓岩，袁俊泉，等.两种基于MIMO雷达体制的鲁棒CFAR检测器［J］.电子与信息学报，2009，31(3):596-600.Wang Dunyong，Ma Xiaoyan，Yuan Junquan，et al.Two kinds of robust CFAR detector based on MIMO radar system［J］.Journal of Electronics ＆ Information Technology，2009，31(3):596-600.

［9］ 王敦勇，马晓岩，袁俊泉，等.一种基于有序统计的MIMO雷达CFAR检测器［J］.现代雷达，2009，31(7):50-54.Wang Dunyong，Ma Xiaoyan，Yuan Junquan，et al.A CFAR detector of MIMO radar based on ordered statistics［J］.Modern Radar，2009，31(7):50-54.

［10］ 戴喜增，彭应宁，汤 俊.MIMO雷达检测性能［J］.清华大学学报:自然科学版，2007，47(1):88-91.Dai Xizeng，Peng Yingning，Tang Jun.Detection performance of MIMO radar［J］.Journal of Tsinghua University:Science and Technology，2007，47(1):88-91.

［11］ Guan Jian，Huang Yong.Detection performance analysis for MIMO radar with distributed apertures in Gaussian colored noise［J］.Science in China Series F:Information Sciences，2009，52(9):1689-1696.

［12］ Kraut S，Scharf L L.The CFAR adaptive subspace detector is a scale-invariant GLRT［J］.IEEE Transactions on Signal Processing，1999，47(9):2538-2541.

［13］ Kraut S，Louis L S，McWhorter L T.Adaptive subspace detectors［J］.IEEE Transactions on Signal Processing，2001，49(1):1-16.

［14］ 关 键.多传感器分布式恒虚警率(CFAR)检测算法研究［D］.北京:清华大学，2000.Guan Jian.Study of distributed constant false alarm rate［D］.Beijing:Tsinghua University，2000.

［15］ 复旦大学.概率论［M］.北京:高等教育出版社，1995.Fudan University.Probability［M］.Beijing:Higher Education Press，1995.