利用广义内积值迭代加权的空时协方差矩阵估计方法

郭佳佳 廖桂生 杨志伟 杜文韬

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引言

由于存在地杂波的干扰，机载下视雷达对慢速运动目标的检测能力较差，而空时自适应处理(STAP)能够有效地分离杂波与目标信号。最优STAP处理需要准确地知道待检测单元杂波的空时协方差矩阵。在实际情况中，杂波协方差矩阵是未知的，通常需要估计获得。而且，杂波环境往往是非均匀的[1,2]，一方面是由于地形本身的特点[3]；另一方面是由阵列的几何结构造成[4]。此时，不同距离门的杂波样本不再满足独立同分布条件，且难以获得两倍以上自由度的均匀样本数，利用最大似然方法估计获得的杂波协方差矩阵与待检测单元的失配，使STAP性能下降[5]。

针对非均匀杂波造成的STAP性能下降问题，目前主要有3类解决方法：第1类是采用降维(RD)或降秩(RR)变换[6]降低自适应处理器的系统自由度，缓解对训练样本数的要求，提高了自适应算法的收敛速度；第2类是寻求统计的方法选取与待检测单元统计相似的训练单元，典型方法如广义内积(GIP)[7,8]、关联维数[9]等；第 3类是在算法设计过程中利用先验信息[10,11]，如结合先验知识和贝叶斯模型的方法[5,12]，但该类方法的性能依赖于先验知识及其精确程度。当先验知识及其精确程度不足时该类方法性能下降[13]。

在不依赖于先验知识且简单可行的前提下，上述第2类方法中基于GIP的样本挑选方法获得了广泛应用。传统GIP方法[7,14,15]需要初始化所谓的“均匀”杂波协方差矩阵进行样本挑选，但是在非均匀环境下，模型失配导致样本筛选不合理，协方差估计性能下降。文献[16]提出的迭代GIP方法也只是重复利用GIP进行样本筛选，通常会导致最终可用样本不足，且同样依赖于初始均匀杂波的协方差矩阵。文献[17]提出了依据广义内积值与理论均值的距离对样本进行自适应加权的协方差矩阵估计方法，能缓解可用样本不足的问题。但是，该方法需要选取相对均匀的场景来估计初始协方差矩阵，若初始协方差矩阵存在误差，加权值无法正确反映样本的非均匀程度，协方差矩阵估计精度下降。

为了解决上述问题，本文提出利用GIP迭代加权的空时协方差矩阵估计方法。该方法利用广义内积值与其统计均值的差距对所有训练样本进行自适应的加权处理，并采用迭代的方式更新权值，从而避免了样本剔除带来的潜在性能下降的问题。同时为了缓解非均匀样本的广义内积值对广义内积均值的影响，本文采用建立广义内积值概率分布直方图的方式对参与计算广义内积均值的样本进行自适应的选择。仿真结果表明本文方法在非均匀环境下具有良好的协方差估计性能。

2 信号模型

图1为机载阵列雷达正侧视示意图。载机沿X轴飞行，速度为v，高度为H。雷达天线是由N个阵元组成的均匀线阵，阵元间隔为半波长，以原点处的阵元作为参考，其它阵元与其距离分别表示为β和θc分别表示杂波地块相对于阵列的方位角，俯仰角和空间锥角。

设一个相干处理间隔(CPI)内，每个阵元接收脉冲数为K。则每个距离单元雷达接收的回波数据可以表示为

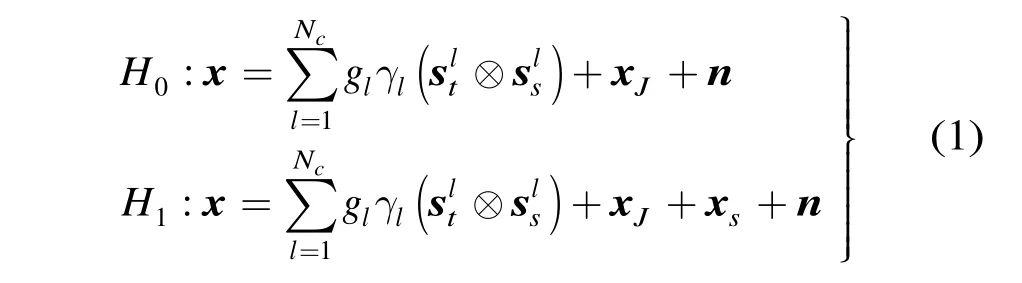
图1 正侧视示意图

其中H表示共轭转置，R为杂波协方差矩阵，s为信号的空时导向矢量。

式(2)中，协方差矩阵R一般是未知的，需要通过估计获得。在实际的情况中，由于密集目标干扰、海陆交界等复杂的因素，STAP涉及的检测环境往往是非均匀的。这时，基于极大似然方法估计的协方差矩阵存在误差，进而导致利用式(2)进行空时处理时，STAP性能下降。因此，非均匀环境下准确估计杂波协方差矩阵是应用空时自适应处理的关键。

3 加权迭代方法

针对非均匀杂波环境下的相关矩阵估计问题，采用基于广义内积值的样本挑选方法及其改进的迭代方法能够缓解样本污染问题，提高杂波协方差矩阵的估计精度。不过，此类方法依赖杂波协方差矩阵的初始估计值，如果初始估计值存在较大误差，则难以挑选出有效样本；此外，空时自适应处理需要大量的训练样本来精确地估计杂波协方差矩阵，简单地剔除方法将减少训练样本的个数，造成检测性能下降。

为解决上述问题，下面采用加权方式来估计协方差矩阵，为便于分析，这里假设环境由两部分区域组成。

由式(5)知，最优权的分子只与均匀样本有关，在样本一定时，最优权与非均匀程度成反比。从而可以得出非均匀程度越大，非均匀样本所加的权值应越小。

由文献[7]知，广义内积值与广义内积均值的差距越大非均匀性越强，且在有限样本下，广义内积的均值不再是理论均值[13]。

经过上述分析，本文利用样本广义内积值与其统计均值的差距对所有样本进行变加权处理，降低相对“非均匀”样本在杂波协方差矩阵中的比重，从而改善样本剔除造成的估计精度下降问题。为缓解非均匀的“坏点”对广义内积统计均值的影响，本文通过建立广义内积直方图来辅助计算广义内积统计均值。考虑到有限样本数下协方差矩阵估计存在误差，本文采用迭代模式进一步地提高杂波协方差矩阵的估计精度。本方法的流程图如图2所示：

下面详细介绍本文方法的主要步骤：

(1)设置初始协方差矩阵： 使用传统的样本协方差矩阵(SCM)方法估计初始杂波协方差矩阵：

其中M为总的训练样本个数。

图2 算法流程图

(2)计算广义内积值并统计其概率分布情况：首先利用获得的协方差矩阵计算各个样本单元的广义内积值zi：

其中是第j次迭代获得的杂波协方差矩阵，初始迭代计算时利用矩阵。

然后通过直方图统计获得广义内积值的概率分布P(zi),i= 1 ,2,… ,M。

(3)计算权值：所有样本的权值是通过计算其广义内积值与广义内积均值之间的差距获得的，因此合理权值的关键在于获得反映均匀数据的广义内积均值。

一般情况下，可认为训练样本中均匀数据占主要部分，非均匀数据相对较少，同时由于均匀数据的广义内积值近似程度较高，与非均匀数据的广义内积值有着明显的差异，因此在广义内积值的统计概率分布中，均匀数据的概率应大于非均匀数据。

根据上述分析，为获得合理的广义内积均值，避免非均匀样本的广义内积值对均值的影响，仅使概率大的样本参与均值的计算。

综上，本文采用GIP概率直方图对样本数据自适应加权迭代方法，提高了协方差矩阵的估计精度，改善系统的检测性能。

4 仿真实验

下面通过计算机仿真来验证本文方法的有效性。仿真参数设置为：天线阵为8个阵元的正侧视理想均匀线阵，阵元间距d=λ/2，机载高度H=8 km，机载的速度v=140 m/s，雷达工作波长λ=0.23 m，相干时间内的脉冲数K=8，雷达的重复频率fr=2500 Hz。

为分析方法性能，首先给出输出信杂噪比(SCNR)的计算式：

式中Rs为目标信号的协方差矩阵，Rcn为杂波加噪声的协方差矩阵。定义输出SCNR损失为自适应处理输出SCNR与最优权处理输出SCNR最大值的差。

仿真对比了文献[17]方法和传统GIP方法[7,8]，其中将文献[17]的方法记为一次加权算法。传统GIP方法是通过杂波单元 GIP与理论均值进行比较，剔除偏离均值较大的样本。

(1)连续非均匀场景 非均匀的样本由来自 4个不同杂波区域的数据组成。样本个数为 640，其中各个区域所占比例分别为0.55, 0.10, 0.20, 0.15；杂噪比分别为35 dB, 45 dB, 60 dB, 60 dB。各个区域的杂波协方差矩阵不同，分别表示为R1,R2,R3,R4，其中R1与待检测单元的杂波协方差矩阵相同。对R1添加扰动产生其它3个区域的协方差矩阵i= 2 , 3, 4，其中⊙表示Hadamard矩阵乘积，ti表示高斯随机矢量，均值为1，方差分别为0.1, 0.4, 1.0。各区域杂波数据由式(12)产生。

其中Ri为杂波协方差矩阵，v为复高斯随机矢量(满足均值为0，协方差矩阵为单位阵I)。

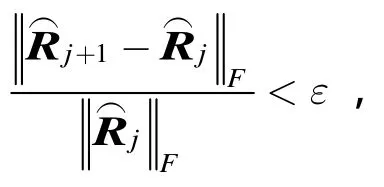
图4是一次加权方法和本文方法收敛时各区域的权值分布对比图。分别对样本进行编号，1~352为第1区域，353~416为第2区域，417~544为第3区域，545~640为第4区域。图4(a)显示一次加权方法虽然利用了所用样本，但是第2区域和第3区域的权值均大于第1区域。可见，一次加权方法不能有效地根据样本的非均匀程度进行差别加权。在图4(b)中第2区域的权值小于第1区域，第3区域和第4区域的权值则明显小于第1区域，即非均匀程度越大加权值越小，说明本文方法能够有效地对样本进行差别加权。

图5给了输出SCNR损失随归一化多普勒频率变化的曲线。图5中，传统GIP方法的性能略差于SCM方法，这是由大量的剔除样本和不合理的样本选择造成的。一次加权方法和SCM方法性能近似。而本文方法可以有效地改善协方差的估计精度，减少性能损失。

图6是非均匀程度与本文方法迭代收敛次数之间的关系。横坐标表示非均匀样本与均匀样本的杂噪比之差；纵坐标表示非均匀样本占总样本数量的比例，基于均匀样本占主要部分的原则，纵坐标最大值应小于 0.5。由图 6可知，当非均匀样本数增大时，迭代收敛次数增加。在非均匀样本数一定时，迭代次数随着非均匀样本的CNR的增加略有减少。这是因为当非均匀样本的CNR增加时，非均匀样本的广义内积值偏离广义内积均值的差距变大，其权值更小，协方差矩阵收敛更快。

(2)离散的非均匀场景 阵列回波快拍中存在多个类目标而形成离散非均匀场景。设有201个距离单元，11个目标点。目标离散地等距离地分布在距离单元56至156之间，信噪比依次递增。目标信号归一化多普勒频率2fd/fr在0.4左右取值，目标空间角cosθc= 0 。杂噪比为40 dB。

图3 加权迭代方法收敛曲线

图4 一次加权方法和迭代加权方法权值分布对比

图7给出的是本文方法收敛时各距离单元的样本权值。仿真时以中间目标所处的距离单元为待检测单元。可以看到，10个存在干扰的距离单元样本的权值相对非常小，且随着干扰强度的增大而减小，达到了依据非均匀样本非均匀程度加权的效果。

图8为输出SCNR损失曲线。仿真结果表明传统的GIP方法在归一化多普勒频率0.2~0.6处出现很大的输出SCNR损失。图8中本文方法的性能和最优处理的性能近似，可以得到很好的输出效果。

5 总结

杂波协方差矩阵估计是空时自适应处理的关键。在非均匀的环境下，基于最大似然的样本协方差矩阵估计方法不再适用。针对非均匀环境下的杂波协方差矩阵的估计问题，本文在建立GIP概率分布直方图的基础上提出迭代加权的协方差估计方法。通过计算样本广义内积值与其统计均值的差距对所有样本进行加权处理，并通过迭代的方式提高杂波协方差矩阵的估计精度，有效解决了基于GIP样本筛选方法存在的潜在性能下降的问题。仿真结果表明本文方法在非均匀环境中可以得到很好的协方差矩阵估计性能。

图5 输出SCNR损失对比

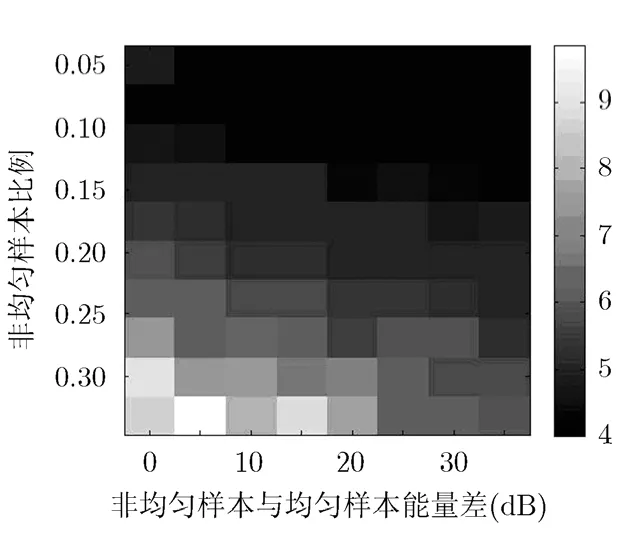
图6 非均匀程度与迭代收敛次数之间的关系

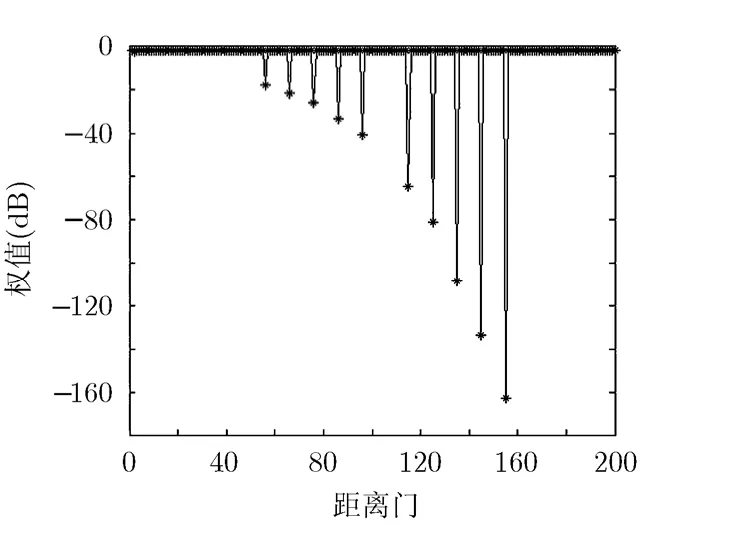
图7 迭代收敛时各距离单元的样本权值

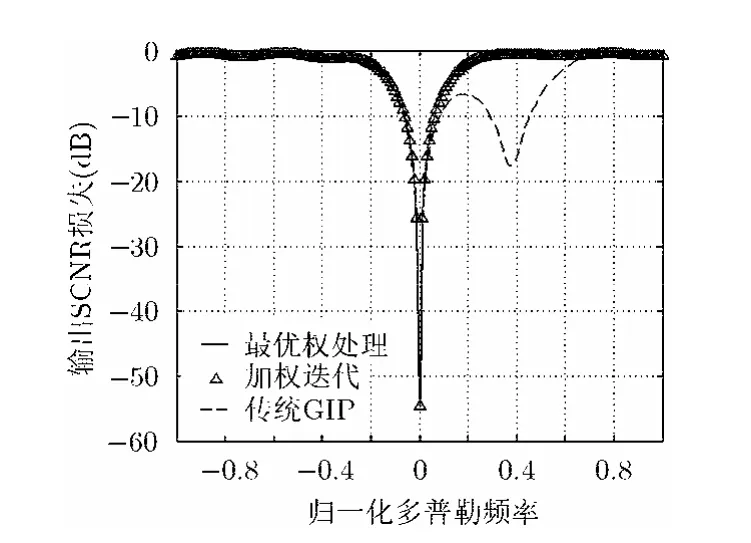
图8 传统GIP方法和本文方法的性能比较

[1] Melvin W L. A STAP overview[J].IEEE Aerospace Electronic Systems Magazine, 2004, 19(1): 19-35.

[2] 周宇, 张林让, 刘楠, 等. 非均匀环境下利用杂波脊信息的杂波滤除方法研究[J]. 电子与信息学报, 2010, 32(6): 1332-1337.Zhou Yu, Zhang Lin-rang, Liu Nan,et al.. Study on exploring knowledge of the clutter ridge for clutter suppression in heterogeneous environments[J].Journal of Electronics&Information Technology, 2010, 32(6): 1332-1337.

[3] Besson O, Bidon S, and Tourneret J Y. Covariance matrix estimation with heterogeneous samples[J].IEEE Transactions on Signal Processing, 2008, 56(3): 909-920.

[4] Bidon S, Besson O, and Tourneret J Y. A bayesian approach to adaptive detection in nonhomogeneous environments[J].IEEE Transactions on Signal Processing, 2008, 56(1):205-217.

[5] Reed I S, Mallett J D, and Brennan L E. Rapid convergence rate in adaptive arrays[J].IEEE Transactions on Aerospace and Electronic Systems, 1974, 10(6): 853-863.

[6] Fa Rui and de Lamare R C. Reduced-rank STAP algorithms using joint iterative optimization of filers[J].IEEE Transactions on Aerospace and Electronic Systems, 2011,47(3): 1668-1684.

[7] Melvin W L and Wicks M C. Improving practical space-time adaptive radar[C]. IEEE National Radar conference on Aerospace and Components, Syracuse, NY, 1997: 48-53.

[8] Yang Xiao-peng, Liu Yong-xu, Hu Xiao-na,et al.. Robust generalized inner products algorithm using prolate spheroidal wave functions[C]. Radar Conference(RADAR)on Aerospace, Components and Signal Processing, Atlanta,GA, 2012: 581-584.

[9] Wang Yong-liang, Chen Jian-wen, Bao Zheng,et al.. Robust space-time adaptive processing for airborne radar in nonhomogeneous clutter environments[J].IEEE Transactions on Aerospace and Electronic Systems, 2003,39(1): 70-81.

[10] Zhu Xu-min, Li Jian, and Stoica P. Knowledge-aided space-time adaptive processing[J].IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1325-1336.

[11] 高永婵, 廖桂生, 朱圣棋, 等. 一种有效色加载因子的知识辅助STAP方法[J]. 电子学报, 2012, 40(10): 2101-2106.Gao Yong-chan, Liao Gui-sheng, Zhu Sheng-qi,et al.. A knowledge-aided STAP approach with effective color loading factors[J].Acta Electronica Sinica, 2012, 40(10): 2101-2106.

[12] 谢洪森, 邹鲲. 一种非均匀场景符合高斯杂波背景下的自适应检测器[J]. 电子与信息学报, 2011, 33(10): 2433-2437.Xie Hong-sen and Zou Kun. An adaptive detector in compound Gaussian clutter of nonhomogeneous environments[J].Journal of Electronics & Information Technology, 2011, 33(10): 2433-2437.

[13] 吴迪军, 徐振海, 熊子源, 等. 机载雷达极化空时联合域杂波抑制性能分析[J]. 电子学报, 2012, 40(7): 1429-1433.Wu Di-jun, Xu Zhen-hai, Xiong Zi-yuan,et al.. Performance analysis of polarization-space-time joint domain processing for clutter suppression in airborne radars[J].Acta Electronica Sinica, 2012, 40(7): 1429-1433.

[14] Rangaswamy M, James H M, and Himed B. Statistical analysis of the non-homogeneity detector for STAP applications[J].Digital Signal Processing, 2004, 14(3):253-267.

[15] Yang Xiao-peng, Liu Yong-xu, and Long Teng. Robust non-homogeneity detection algorithm based on prolate spheroidal wave functions for space-time adaptive processing[J].IET Radar, Sonar&Navigation, 2013, 7(1):47-54.

[16] Schoening G N, Picciolo M L, Mili L,et al.. Adaptive processor convergence improvement using reiterative projection statistics[C]. 2006 IEEE Radar conference on Aerospace, Devices and Systems, Verona, NY, 2006:725-730.

[17] 曾操, 廖桂生, 杨志伟, 等. 基于样本加权的三通道SAR-GMTI机载数据处理及性能分析[J]. 电子学报, 2009,37(3): 506-512.Zeng Cao, Liao Gui-sheng, Yang Zhi-wei,et al.. Airborne data processing and performance analysis based on three aperture SAR GMTI system using weighted sample[J].Acta Electronica Sinica, 2009, 37(3): 506-512.