基于周期分区的相控阵雷达任务交叉调度研究

叶朝谋 丁建江 俞志强 蔡 轶



基于周期分区的相控阵雷达任务交叉调度研究

叶朝谋*①②丁建江①俞志强①蔡 轶①

①(空军预警学院 武汉 430019)②(中国人民解放军95112部队 佛山 528227)

传统相控阵雷达任务调度算法中，各单驻留任务不可分割，发射与接收之间的空闲等待时间未被有效利用，系统调度能力受限。针对此问题，该文在深入分析交叉规则及选取策略的基础上，提出一种基于采样周期最大公约数分区的任务实时交叉调度(PDI)算法，其可解决交叉调度过程中任务因采样周期不同而产生冲突的难题，该文还分析了调度算法流程，交叉算法流程及过载处理等。仿真结果表明，该算法可大幅提高系统调度的负载能力，调度性能明显优于传统算法。

相控阵雷达；资源管控；任务交叉调度

1 引言

相控阵雷达波束快速扫描与波形捷变等技术优势的充分发挥需要解决好资源优化管理这一难题，驻留任务调度则是其中最为关键的技术之一。相关研究成果较多，如文献[1]提出的混合遗传调度算法具有较好性能但计算要求高。文献[2]提出的基于时间窗算法具有任务延迟控制优势。文献[3,4]通过综合两个属性参数得到任务综合优先级，使系统具有更高的调度能力。文献[5]提出的时长可变调度算法使任务调度更为灵活，调度能力得到提升。文献[6]提出了一种多波束情况下的整数规划模型及调度算法。然而，上述传统任务调度方法中发射与接收之间的空闲等待时间未得到有效利用，因此系统最大调度负载能力受到限制。

针对上述不足，文献[7]首次提出的交叉调度思想有效利用了空闲等待时间，从而可进一步提高系统调度能力。后续相关研究也取得了若干成果，如文献[8]提出的基于优先级交叉算法使得系统调度能力得到一定程度的提高；文献[9,10]针对同时接收多波束的情形，提出的基于优先级的交叉调度算法也取得了较好的性能。文献[11,12]提出了宏观上的任务交叉调度规划方法；文献[13]则在其基础上提出了基于效益的交叉调度算法，但该算法任务时间窗要求高。文献[14]针对同时多波束能力的多普勒相控阵雷达，提出了相应的整数规划模型与交叉调度算法。另外，文献[15-17]分别提出的基于拉格朗日松弛技术算法、贪婪算法、基于时间指针算法在调度性能上均有所提高。但上述交叉调度方法仍未能有效解决任务因采样周期不同而产生冲突的问题。针对此问题，本文提出一种基于周期分区的任务实时交叉调度算法，可有效解决上述难题。

2 任务模型

2.1 交叉调度驻留任务描述

2.2 搜索任务模型

设搜索区域分为B个搜索波位，可得到该区域搜索任务模型为

各驻留请求到达时间与截止期关系分别为

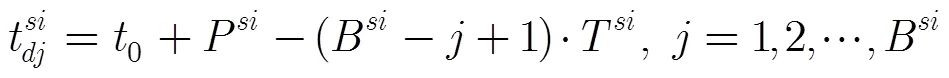
2.3 跟踪任务模型

设跟踪任务模型为

其中B表示对目标的跟踪采样次数。

设发现目标后立即发射一个验证驻留，且验证驻留后的首个跟踪驻留请求间隔时间可取为小于该类目标跟踪采样周期的任意值，则该目标各驻留请求到达时间与截止期的关系为

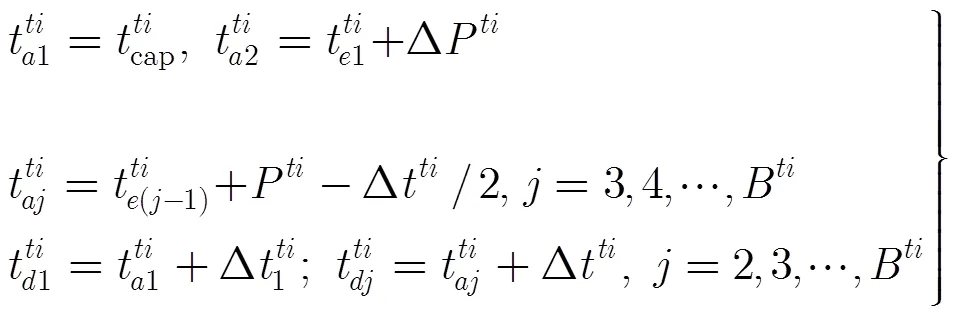
3 驻留任务交叉规则

图1 非包含关系时交叉规则

4 任务调度算法

4.1 算法基本思想

将各P平分为N个长度为gcd的标准区间

再对标准区间进一步平分为Ns个标准调度分区间(记为Plot)，则有Plot=Pgcd/Ns，

4.2 算法实现流程

各类任务在调度过程中将按标准调度分区间进行调度，具体算法实现流程如图4所示。

步骤5 对有新任务加入的任务子集进行交叉，计算交叉后的占用时间长度；

步骤6 进行负载分析与过载处理，若过载，则删除部分低优先级任务；

步骤8 该标准调度分区间结束，转入下一标准调度分区间。

图3 基于周期分区的任务调度关系

图4 基于周期分区的任务交叉调度流程图

4.3 任务交叉流程

通常，系统还要求满足时间与能量的限制条件，可分别近似表示为[11]

(10)

5 调度负载分析

定义任务时间占用率为任务集实际调度过程中占用时间与采样周期的比值。根据前面建立的任务模型及算法，可得

某P类的跟踪任务时间占用率为

某区搜索任务的时间占用率为

任务总时间占用率为

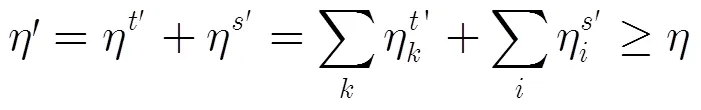
6 仿真结果与分析

仿真条件：设3类目标任务参数如表1所示，表中为初始值且其值根据目标所处距离范围分段计算；仿真时间为150 s，目标均向站直线飞行，调度间隔为最小时间窗，各类目标随机产生，各目标直到仿真结束才消失；任意1 s内的平均发射时间小于400 ms，能量消耗小于200 kJ。图6为1类与2类目标数固定时，PDI算法在较小时间窗时与某经典算法(HPI)[16]最大负载能力对比，图7为PDI在较小时间窗时与HPI算法的调度性能对比，图8为PDI算法在不同时间窗条件下的调度性能对比；图6~图8中，PDI算法的各类跟踪任务小时间窗取值分别为30 ms, 50 ms, 60 ms，大时间窗分别为50 ms, 100 ms, 150 ms, HPI算法的时间窗为采样周期。

仿真结果分析：

(1)由图6可知，当满足采样周期整数倍关系的1类与2类目标数越小时，PDI算法最大负载率越高于HPI算法；两个算法的最大负载率明显高于非交叉算法的理论最大负载能力100%。

(2)由图7可知，HPI算法未发生调度失败，但时间窗要求为采样周期，实际中难以满足；PDI算法当新目标在较短时间内集中大量产生时，发生了新任务调度失败现象，但能满足较严格时间窗要求且系统负载率大于HPI算法。

表1雷达任务参数表

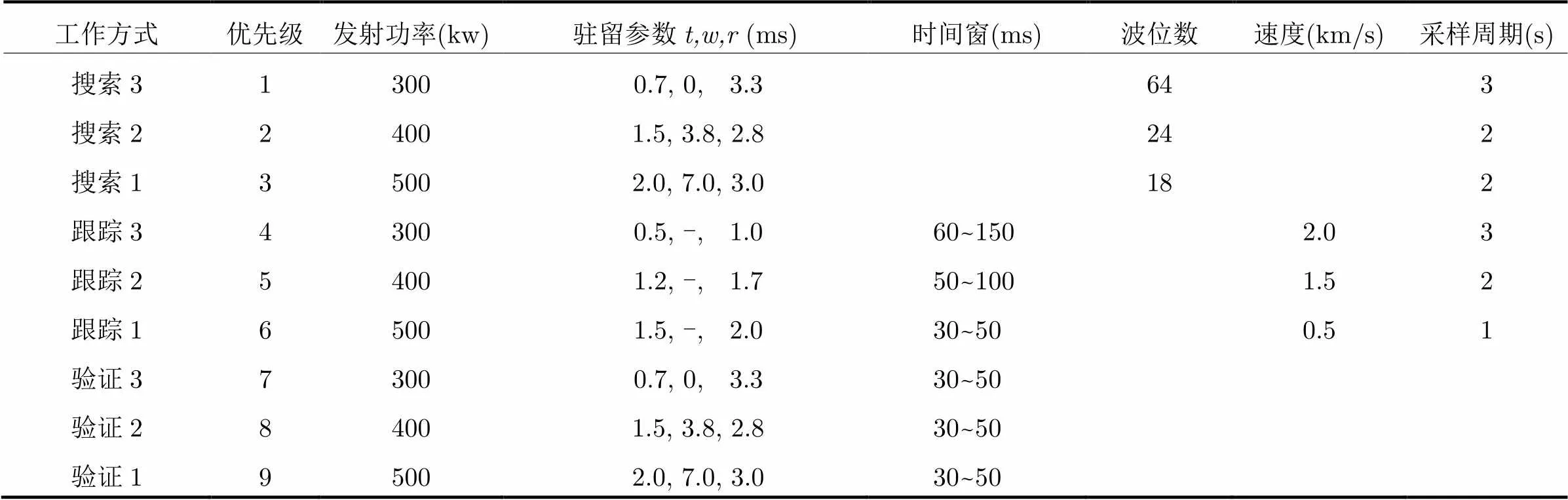
工作方式优先级发射功率(kw)驻留参数t,w,r (ms)时间窗(ms)波位数速度(km/s)采样周期(s) 搜索313000.7, 0, 3.3643 搜索22400 1.5, 3.8, 2.8242 搜索13500 2.0, 7.0, 3.0182 跟踪343000.5, -, 1.060~1502.03 跟踪254001.2, -, 1.750~1001.52 跟踪165001.5, -, 2.030~500.51 验证373000.7, 0, 3.330~50 验证28400 1.5, 3.8, 2.830~50 验证19500 2.0, 7.0, 3.030~50

注：“-”表示跟踪方式时，是可以变的。

(3)由图8可知，PDI算法具有较好的时间窗适应性，在更小的时间窗条件下性能无明显下降；且负载饱和时系统可按优先级进行过载任务删除。

图6 1类，2类目标数固定时最大负载率对比

7 结束语

本文针对传统相控阵雷达任务调度方法最大负载能力受限的问题，提出了一种基于采样周期最大公约数分区的实时任务交叉调度算法，该算法可解决任务调度时因采样周期不同而产生冲突的难题，从而进一步提高了系统调度能力。仿真结果表明，该算法是有效可行的，可应用于相控阵雷达调度器设计，且对一般实时调度系统也有参考价值。

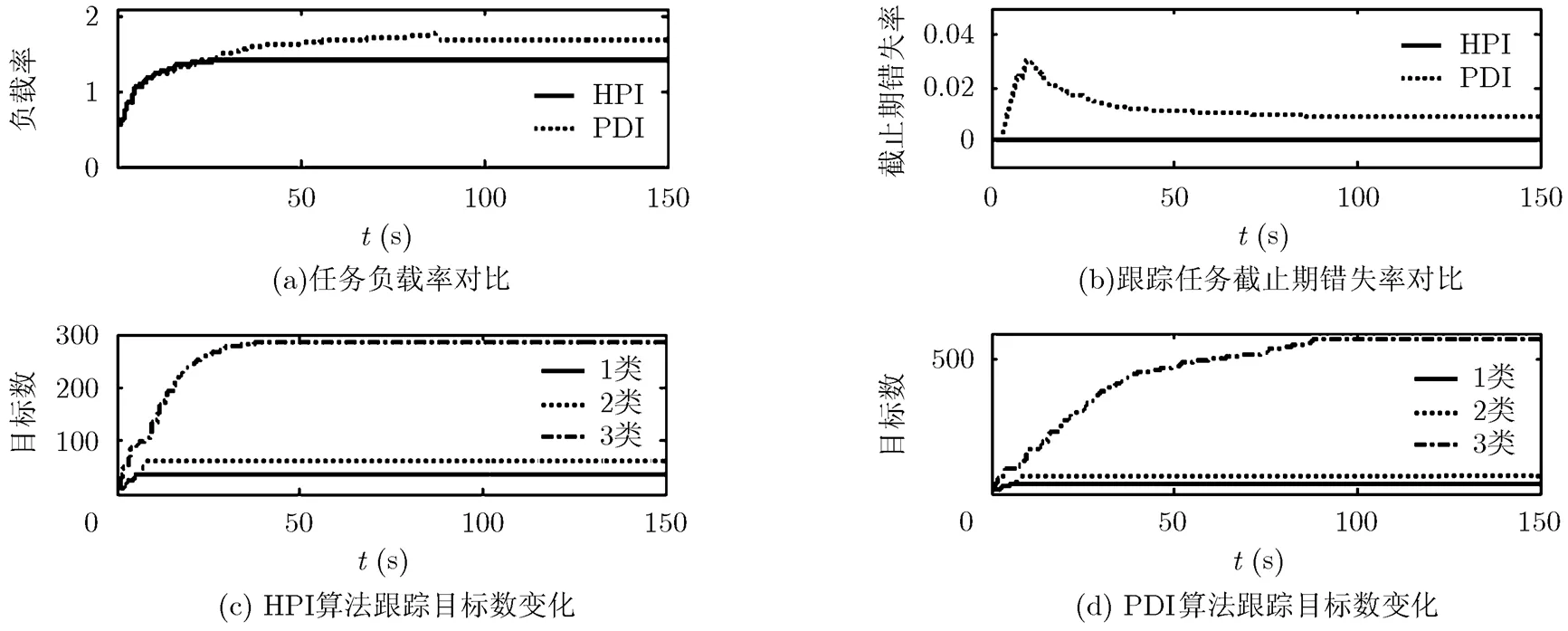
图7 调度性能对比

图8 PDI不同时间窗时的调度变化

[1] 周颖, 王国玉, 王雪松, 等. 基于启发式混合遗传算法的相控阵雷达最优化调度[J]. 系统工程与电子技术, 2006, 28(7): 992-996.

Zhou Ying, Wang Guo-yu, Wang Xue-song,. Optimal scheduling using hybrid GA with heuristic rules for phased array radar[J]., 2006, 28(7): 992-996.

[2] Jang D S, Choi H L, and Roh J E. A time-window-based task scheduling approach for mutlifunction phased array radars[C]. 11th International Conference on Control, Automation and Systems, KINTEX, Gyeonggi-do, Korea, 2011: 1250-1255.

[3] 卢建斌. 相控阵雷达资源优化管理的理论与方法[D]. [博士论文], 国防科学技术大学, 2007.

Lu Jian-bin. Theory and method of resource optimization and management for phased array radars[D]. [Ph.D. dissertation], National University of Defense Technology, 2007.

[4] Lu Jian-bin, Xiao Hui, Xi Ze-min,.. Phased array radar resource management: task scheduling and performance evaluation[J]., 2013, 9(3): 1131-1138.

[5] Mir H and Abdelaziz F B. Cyclic task scheduling for multifunction radar[J]., 2012, 9(3): 529-537.

[6] Chen Jie, Tian Zhon, Wang Lei,.. Adaptive simultaneous multi-beam dell scheduling algorithm for multifunction phased array radars[J].&, 2011, 8(14): 3051-3061.

[7] Farina A and Neri P. Multitarget interleaved tracking for phased array radar[J]., 1980, 127(4): 312-318.

[8] Izquierdo-Fuente A and Casar-Corredera J R. Approach to multifunction radar scheduling simulation[C]. IEEE National Telesystems Conference, San Diego, CA, 1994: 67-70.

[9] Cheng Ting, He Zi-shu, and Li Hui-yong. Adaptive dwell scheduling for digital array radar based on online pulse interleaving[J]., 2009, 18(3): 574-578.

[10] Cheng Ting, He Zi-shu, and Tang Ting. Novel radar dwell scheduling algorithm based on pulse interleaving[J]., 2009, 20(2): 247-253.

[11] Lee C G, Kang P S, Shih C S,. Radar dwell scheduling considering physical characteristics of phased array antenna [C]. IEEE Real-Time Systems Symposium, Cancun, Mexico, 2003: 14-24.

[12] Lee C G, Kang P S, Shih C S,.. Schedulability envelope for real-time radar dwell scheduling[J]., 2006, 55(12): 1599-1613.

[13] Lee C G. A novel framework for quality-aware resource management in phased array radar systems[C]. Proceedings of the 11th IEEE Real Time and Embedded Technology and Applications Symposium, San Francisco, 2005: 322-331.

[14] Jang D S and Choi H L. Heuristic pulse interleaving algorithms for multi-target tracking on pulse doppler phased array radars[C]. IEEE International Conference on Radar, Atlanta, GA, 2012: 558-563.

[15] Elshafei M, Shirali H D, and Smith J C. Radar pulse interleaving for multi-target tracking[J]., 2004, 51(1): 72-94.

[16] Mir H S and Wilkinson J D. Task scheduling algorithm for an air and missile defense radar[C]. IEEE Radar Conference, Rome, 2008: 1-6.

[17] Xie Xiao-xiao, Zhang Wei, and Chen Ming-yan. A novel time pointer-based fast radar pulse interleaving algorithm[C]. 5th International Congress on Image and Signal Processing, Chongqing, 2012: 1870-1874.

叶朝谋： 男，1980年生，博士生，研究方向为雷达组网资源管控.

丁建江： 男，1963年生，教授，博士生导师，主要研究方向为雷达组网、目标智能检测与识别.

俞志强： 男，1964年生，教授，主要研究方向为雷达系统与目标识别.

Study on Task Interleaving Scheduling of Phased Array Radar Based on Period Division

Ye Chao-mou①②Ding Jian-jiang①Yu Zhi-qiang①Cai Yi①

①(430019,)②(95112528227,)

The waiting time between transmitting and receiving time is not used in conventional task scheduling methods for phased array radar in which dell is impartible, thus system scheduling capacity is restrained. Based on analysis of dell interleaving rules and rule selection guidelines, a dell interleaving scheduling algorithm is proposed based on sampling period division, which can solve the task confliction issue caused by different sampling periods. The scheduling flow, interleaving flow and tactic for overload are also analyzed. The simulation results show that the proposed algorithm improves scheduling capability greatly and achieves better performance compared with conventional task scheduling algorithm.

Phased radar; Resource management; Task interleaving scheduling

TN958

A

1009-5896(2014)02-0435-06

10.3724/SP.J.1146.2013.00475

叶朝谋 1060623450@qq.com

2013-04-11收到，2013-10-16改回

全军军事学研究生课题(2011JY002-537，2012JY002-602)资助课题