基于波形选择的MIMO雷达三维稀疏成像与角度误差校正方法
2014-05-29廖桂生刘长赞
杨 杰 廖桂生 李 军 党 博 刘长赞
基于波形选择的MIMO雷达三维稀疏成像与角度误差校正方法
杨 杰*廖桂生 李 军 党 博 刘长赞
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
该文研究稀疏目标场景下,波形选择对基于压缩感知理论的MIMO雷达成像效果的影响并提出一种改进的成像角度误差校正方法。首先分析了模糊函数和压缩感知匹配字典的相关系数之间的关系;然后,在空间小角度域情况下,针对成像场景中的角度误差,提出一种改进的基于迭代最小化的稀疏学习(SLIM)算法进行校正。仿真结果表明,选择具有较低旁瓣模糊函数的发射波形可以提高成像质量,改进的SLIM算法可以有效补偿角度误差。
MIMO雷达;稀疏成像;波形选择;角度误差校正;基于迭代最小化的稀疏学习(SLIM)
1 引言
与传统相控阵雷达相比,多输入多输出(MIMO)雷达使用多天线发射多重探测信号照射目标,并利用多天线接收目标反射的后向散射回波信号,可以显著改善参数可辨识性,实现更为灵活的发射方向图设计,改进目标检测和参数估计性能[1]。
本文主要研究窄带单基地MIMO雷达稀疏成像问题。在实际雷达成像场景中,如果目标是稀疏分布的,则成像场景可以进行稀疏表示,而压缩感知作为一种有效的方法,特别适用于这类稀疏问题的求解。文献[2,3]具体研究了压缩感知在雷达系统中的应用,并取得了一些有意义的成果。与传统的基于匹配滤波的成像算法相比,压缩感知算法可以极大地降低数据存储、处理和传输的成本,并且可以以高概率重构出原目标场景,提高分辨率[4,5]。
鉴于压缩感知理论相比传统匹配滤波的优势,文献[6-8]研究了压缩感知在MIMO雷达成像中的应用。在MIMO雷达中,成像区域是关于距离、角度、多普勒的3维空间,相比传统相控阵雷达增加了角度维这一自由度[7],因而目标场景在MIMO雷达的探测空间具有稀疏性,进而可以应用压缩感知算法进行重构。
与传统的匹配滤波算法不同,压缩感知是一种基于凸优化的重构算法,因而能够突破由雷达模糊函数的不确定性准则(uncertainty principle)所引起的成像分辨率限制[9],另一方面,文献[2]已经证明了压缩感知算法的重构效果与匹配字典的最大相关系数之间存在关联。本文首先在此基础上推导出了MIMO雷达发射波形的模糊函数和匹配字典最大相关系数之间的关系;然后,通过对发射波形为线性调频信号和跳频信号的MIMO雷达模糊函数的分析,选择旁瓣较低(成像效果较优)的跳频波形作为发射波形,对距离-角度域成像问题中的角度误差校正方法进行研究。文献[10]提出了一种运算量小,恢复效果好,无需设置正则化参数的压缩感知成像算法—基于迭代最小化的稀疏学习算法(Sparse Learning via Iterative Minimization, SLIM),文献[11]在MIMO雷达的发射信号为线性调频信号、空间角度探测范围较小的情况下,通过将包含角度误差的接收信号进行泰勒一阶近似,并将稀疏模型的匹配字典进行相应修正,得到了适用于存在角度误差的探测场景的改进SLIM算法。本文在文献[10]和文献[11]所提算法的基础上,采用跳频信号作为发射波形,建立起相应的稀疏模型,并对此模型提出了一种基于泰勒二阶近似的改进SLIM算法,相比于文献[11]所采用的算法,本文所提出的算法对角度误差的补偿效果更优。仿真结果验证了本文所推导的波形选择准则和改进SLIM算法的有效性。
2 MIMO雷达模糊函数
2.1 MIMO雷达信号模型

图1 单基地MIMO雷达系统模型

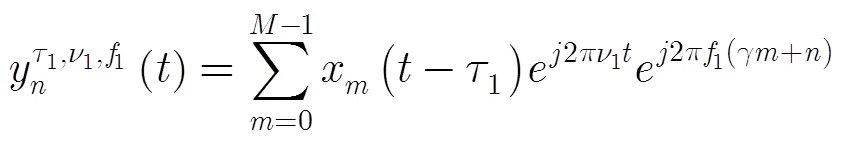

式(2)中,由于等式右端的第1项与发射波形无关,故简化后的MIMO雷达模糊函数为

2.2 跳频波形及线性调频波形的模糊函数
雷达发射信号(解调去载波)的表达式为

在文献[13,14]中,已经推导出了跳频波形的模糊函数的表达式为

对于线性调频波形来说,

对文献[13]中的式(17)稍作修正,容易推导出线性调频信号的模糊函数为

其中

3 MIMO雷达成像场景的稀疏表示




4 MIMO雷达稀疏成像效果与模糊函数的关系

容易推导出下述等式:

同理,容易推得

通过上面的分析,可以给提高基于压缩感知算法的图像重构效果提供一条有效的准则,即选择具有较低旁瓣模糊函数的发射波形(匹配字典的最大相关系数较小),从而得到较好的成像质量。
5 基于改进的SLIM算法的MIMO雷达稀疏成像角度误差校正方法
由第3节的分析可知,当目标在探测区域内稀疏分布时,可以采用压缩感知算法恢复目标场景。此时,如果全部目标恰好位于所划分的探测空间格点上,算法恢复效果较好;但是,由于目标分布的随机性,并不能保证所有目标均位于格点上,这必然会引起格点误差,造成匹配字典中的各列回波信号与目标的真实位置不相对应,成像效果变差。为了减少偏离格点的目标数目,可以减小格点间距,但是这样又会增大匹配字典中各列间的相关性,使其不满足限制等距属性(RIP)条件,同样会使成像效果变差。


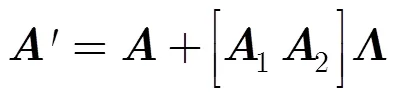
其中
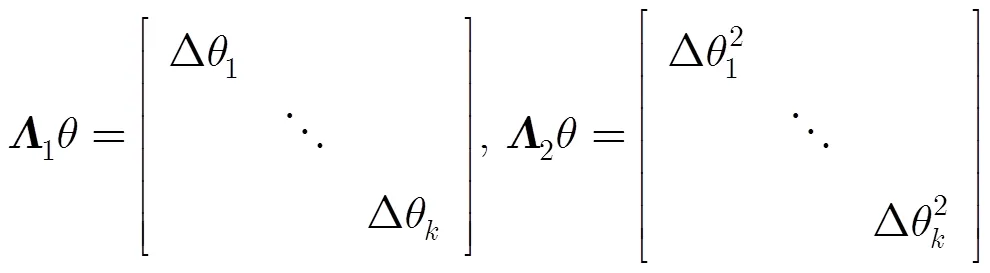
经过以上的推导,可得存在角度误差时的成像模型为


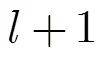
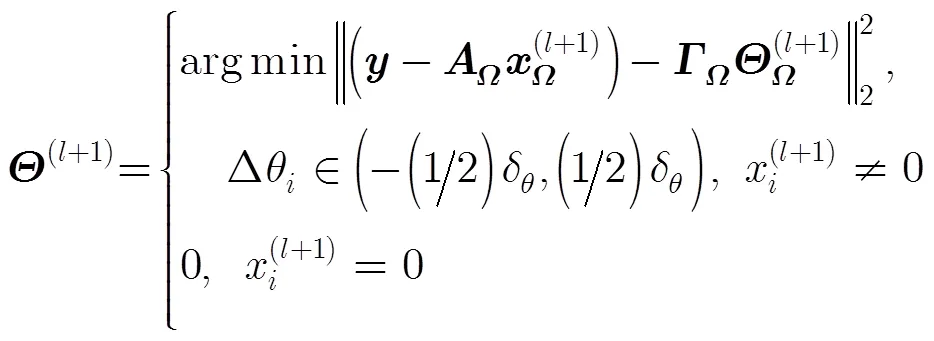
对于式(18)中的极小化问题,可以考虑采用模拟退火算法求解。
6 仿真与分析


仿真2 跳频信号成像效果 目标场景同仿真1,仿真结果如图4,图5所示。
同线性调频信号相比,跳频信号模糊函数最高旁瓣的绝对值较低,因而匹配字典中的最大相关系数较小,压缩感知成像效果也比较好,可以比较精确地恢复出目标在探测区域内的真实位置。
综上可得,MIMO雷达的模糊函数与压缩感知匹配字典的相关系数之间存在关联,模糊函数仍然能够影响基于压缩感知方法的成像效果。因此,在实际成像场合中,波形的选择是个关键的因素。通过选择具有较低旁瓣模糊函数的发射波形,可以减小匹配字典中的最大相关系数,进而可以提高图像反演质量,获得目标在探测区域内的真实位置。
仿真3空间小角度域情况下的角度误差校正
选择跳频信号作为发射波形,对距离-角度域成像场景中的角度误差进行校正。以距离-角度域上的3维图形代表成像结果,图中峰值所对应的位置为反演出的目标位置,峰值的高度代表反演出的目标散射系数,点划线的位置代表真实目标位置,点划线的高度代表真实目标的散射系数值。
仿真结果如图6,图7所示。
对比图6,图7的反演效果可知,对接收数据做二阶泰勒近似,估计出的角度误差比一阶近似情况(文献[11]所采用的算法)下的更加精确。在上面的仿真中,由于对接收信号做了泰勒近似,因此反演出的目标散射系数存在不同程度的衰减。

图2 发射信号为线性调频波时的距离-多普勒域仿真结果

图3 发射信号为线性调频波时的距离-角度域仿真结果

图4 发射信号为跳频波时的距离-多普勒域仿真结果

图5 发射信号为跳频波时的距离-角度域仿真结果

图6 一阶误差校正后的反演图像
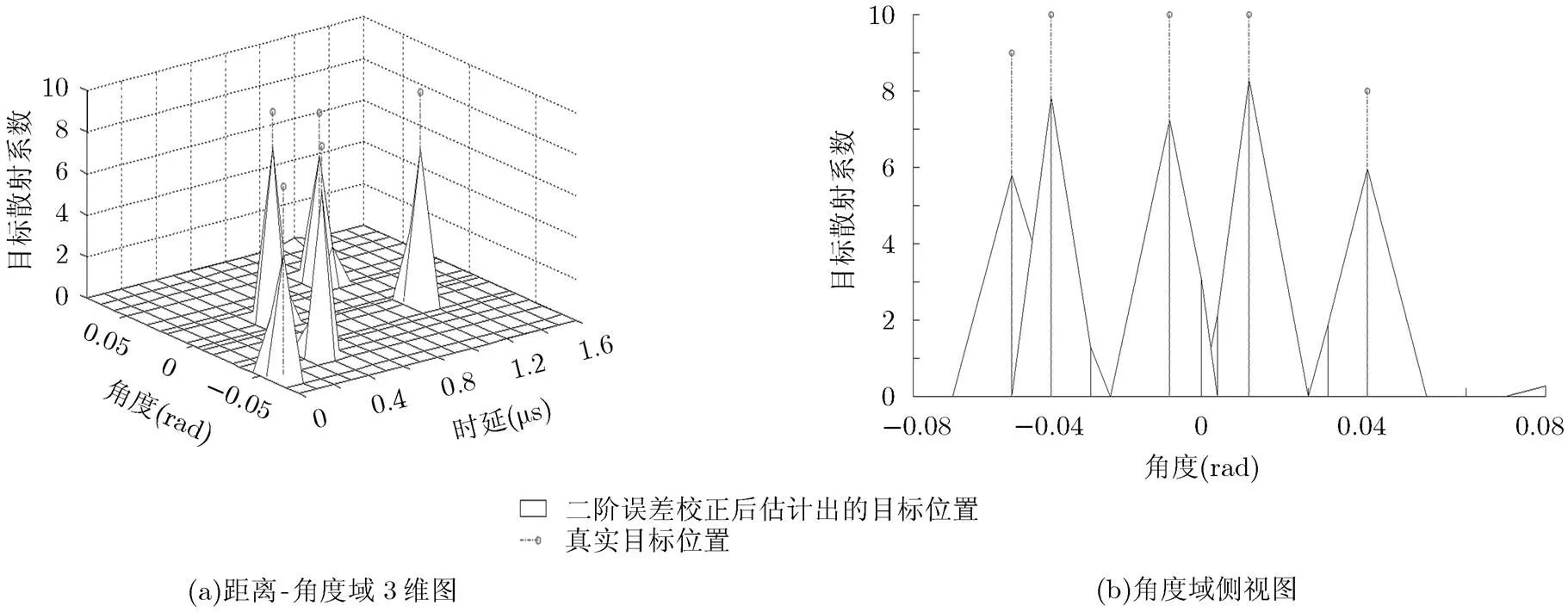
图7 二阶误差校正后的反演图像
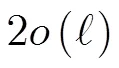
从以上仿真结果可以看出,本文提出的改进的SLIM算法可以有效克服由匹配字典失配引起的成像角度误差。
7 结束语
本文主要从两个方面研究了压缩感知在MIMO雷达成像中的应用:(1)推导出了雷达模糊函数和匹配字典相关系数之间的关系;(2)在空间小角度域情况下,结合模拟退火算法,提出了一种基于改进的SLIM算法的角度误差校正方法。通过对两方面的研究得到以下结论:(1)发射波形模糊函数的旁瓣越高,成像效果越差,因此在实际应用中,为了得到较好的成像效果,应当选择具有较低旁瓣模糊函数的发射波形;(2)实际成像场景中由于匹配字典失配,反演出的目标位置往往存在误差,采用本文提出的改进的SLIM算法,可以准确地补偿空间小角度域情况下的角度误差。仿真结果验证了此算法的有效性。
[1] Fishler E, Haimovich A, Blum R,.. MIMO radar: an idea whose time has come[C]. Proceedings of the IEEE Radar Conference, Philadelphia, USA, 2004: 71-78.
[2] Herman M A and Strohmer T. High resolution radar via compressed sensing[J]., 2009, 57(6): 2275-2284.
[3] 江海, 林月冠, 张冰尘, 等. 基于压缩感知的随机噪声成像雷达[J]. 电子与信息学报, 2011, 33(3): 672-676.
Jiang Hai, Lin Yue-guan, Zhang Bing-chen,.. Random noise imaging radar based on compressed sensing[J].&, 2011, 33(3): 672-676.
[4] Donoho D L. Compressed sensing[J]., 2006, 52(4): 1289-1306.
[5] Candes E J, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]., 2006, 52(2): 489-509.
[6] Strohmer T and Friedlander B. Compressed sensing for MIMO radar-algorithms and performance[C]. Proceedings of the 43rd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, California, 2009: 464-468.
[7] Chen Chun-yang and Vaidyanathan P P. Compressed sensing in MIMO radar[C]. 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, California, 2008: 41-44.
[8] 顾福飞, 池龙, 张群, 等. 基于压缩感知的稀疏阵列MIMO雷达成像方法[J]. 电子与信息学报, 2011, 33(10): 2452-2457.
Gu Fu-fei, Chi Long, Zhang Qun,.. An imaging method for MIMO radar with sparse array based on compressed sensing[J].&, 2011, 33(10): 2452-2457.
[9] Guey Jiann-ching and Bell M R. Diversity waveform sets for delay-doppler imaging[J]., 1998, 44(4): 1504-1522.
[10] Tan Xing, Roberts W, Li Jian,.. Sparse learning via iterative minimization with application to MIMO radar Imaging[J]., 2011, 59(3): 1088-1101.
[11] He Xue-zhi, Liu Chang-chang, Liu Bo,.. Sparse frequency diverse MIMO radar imaging for off-grid target based on adaptive iterative MAP[J]., 2013, 5(2): 631-647.
[12] Friedlander B. On the relationship between MIMO and SIMO radars[J]., 2009, 57(1): 394-398.
[13] Chen Chun-yang and Vaidyanathan P P. MIMO radar ambiguity properties and optimization using frequency- hopping waveforms[J]., 2008, 56(12): 5926-5936.
[14] Badrinath S, Srinivas A, and Reddy V U. Low-complexity design of frequency-hopping codes for MIMO radar for arbitrary Doppler[J]., 2010, DOI: 10.1155/2010/319065.
[15] Gogineni S and Nehorai A. Frequency-hopping code design for MIMO radar estimation using sparse modeling[J]., 2012, 60(6): 3022-3035.
杨 杰: 男,1989年生,博士生,研究方向为MIMO雷达信号处理.
廖桂生: 男,1963年生,教授,博士生导师,研究方向为阵列信号处理、空时自适应处理、动目标检测.
李 军: 男,1972年生,副教授,硕士生导师,研究方向为阵列信号处理、空时自适应处理、多通道雷达信号处理.
Three Dimensional MIMO Radar Imaging Using Sparse Model Based on Waveform Selection and Calibration Method in the Presence of Angle Imperfections
Yang Jie Liao Gui-sheng Li Jun Dang Bo Liu Chang-zan
(,’710071,)
The effect of waveform selection on compressive sensing MIMO radar imaging using sparse model and an improved calibration method in the presence of angle imperfections are researched in this paper. Firstly the relationship between ambiguity function and Compressive Sensing (CS) “dictionary coherence coefficient” is analyzed. Then, in the presence of small spatial angle, an improved method based on “Sparse Learning via Iterative Minimization” (SLIM) algorithm is proposed to calibrate angle errors. Simulation results illustrate that the imaging quality can be enhanced when selected waveforms have low sidelobes and prove that the modifed method can calibrate angle errors effectively.
MIMO radar; Imaging using sparse model; Waveform selection; Angle imperfections calibration; Sparse Learning via Iterative Minimization (SLIM)
TN958
A
1009-5896(2014)02-0428-07
10.3724/SP.J.1146.2013.00500
杨杰 yangjie_xidian@126.com
2013-04-16收到,2013-07-27改回
国家自然科学基金(61271292),国家973计划项目(2010CB731903)和西安电子科技大学基本科研业务费(k50511020003)资助课题
