期望主瓣响应下任意阵方向图综合方法

潘点飞，程乃平

（中国人民解放军装备学院，北京 101416）

1 引言

阵列天线以其独特的性能和形式在雷达、声呐、通信、测控等领域得到了广泛的应用。测控系统一般要求阵列天线方向图具有恒定的主瓣宽度，旁瓣尽可能低，以便降低干扰的影响，实现对目标的精确测量与控制。通过相应算法获得阵列天线的最优权系数，使阵列天线方向图尽可能地满足特殊的主瓣形状和极低的旁瓣电平等要求，称之为阵列方向图综合[1]。

早期对阵列天线方向图综合的研究主要针对均匀分布的各向同性阵元构成的阵列，如均匀线阵[2]、平面阵等[3]。近20年来，对任意阵方向图综合的研究成为热点，归纳起来主要有3种任意阵方向图综合方法：一是基于自适应原理的方向图综合方法[4,5]，二是基于优化理论的方向图综合方法[6~8]，三是基于智能方法的方向图综合方法[9~11]。自适应原理方向图综合法通过引入大量人为干扰来抑制副瓣电平，经迭代运算使方向图的主、副瓣电平满足一定要求。该算法中迭代系数难以确定，收敛速度、收敛稳定性与通用性难以保证。优化理论方向图综合法将阵列方向图综合问题转化为凸优化问题，使综合后方向图的幅度和相位与期望方向图的误差最小。该方法要求方向图的幅度和相位与期望方向图都要达到最小，不必要的相位约束将导致旁瓣电平较高。智能方法方向图综合法采用遗传算法、粒子群算法等智能方法直接对方向图的权向量进行优化，对于特殊形状的期望方向图优化效果往往不理想。

上述常见的任意阵方向图综合方法，通常只考虑主瓣方向固定在期望信号方向上，通过寻找最优权系数使阵列方向图尽可能逼近期望方向图。在实际应用中，如测控系统中，随着目标的移动，要求阵列天线波束能够在不同空间指向上满足指向精度、增益、主瓣宽度等要求，且在干扰方向形成抗干扰零陷。这就对阵列方向图综合方法提出了更高的要求，即在保证不同指向时的主瓣形状和零陷满足要求的同时，尽可能降低旁瓣电平。文献[12]通过LCMV(线性约束最小方差)准则提高了自适应方向图综合法迭代系数的顽健性，但是在不同空间指向上，波束主瓣指向精度与宽度将产生畸变。文献[13]采用二阶锥规划方法对主瓣赋形，同时保证旁瓣电平一致。但对于带有零陷的复杂旁瓣形状，可能导致凸优化的目标函数不再是凸函数。文献[14]提出自适应动态粒子群优化算法，可使共形阵列天线形成多方向图，但没有考虑不同指向角对算法的影响。本文将自适应理论与凸优化方法相结合，通过自适应理论得到满足特殊旁瓣要求的方向图，以此作为旁瓣参考电平，并确定期望主瓣，将阵列方向图综合问题转化为二阶锥规划问题，而后采用凸优化循环迭代方法使不同指向的主瓣形状与期望主瓣一致，同时保证综合后旁瓣形状尽可能逼近自适应理论法得到的结果。

2 基本原理

一定数量的天线阵元按照一定规则排列成天线阵列。设阵元数目为N，第n个阵元坐标为Pn(xn,yn,zn)，在极坐标中可写成Pn(rn,θn,φn)，其中，rn为阵元到原点的距离，φn为俯仰角，θn为方位角。假设信号从远场入射方向为(θ,φ)，到达第一个阵元的相位为零，则阵元n接收信号的相位为

其中，k=-2π/λ,(cosψcosθ, cosφsinθ, sinφ)表示参考阵 元 到 远 场 目 标 的 单 位 矢 量 ，r→(rncosφncosθn,rncosφnsinθn,rnsinφn)表示参考阵元到阵元n的方向矢量。

设第n个阵元接收到的信号为

其中，A、ω0、φ0分别表示信号的幅度、角频率和初始相位。fn(θ,φ)为第n个阵元的方向图。进一步可得到天线阵接收信号为

在阵列结构、信号频率和阵元方向图确定的情况下，V只与信号入射方向有关，称之为导向矢量。若第n个天线单元的加权值为wn，则整个阵列的输出即为

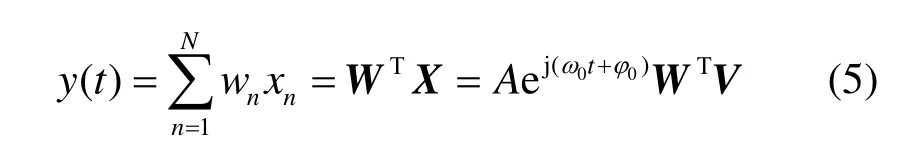
其中，W=[w1,w2,…,wN]T表示阵列加权向量，T表示转置运算，则阵列天线方向图表示为

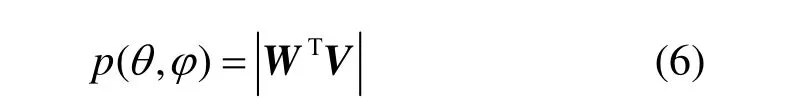
由式(6)可以看出，阵列天线方向图由权值和导向矢量共同决定，而导向矢量与阵元方向图和阵元的排列方式有关。因此，对阵列天线方向图的优化可以通过对阵元方向图、权值和阵元分布的优化获得。对于确定的阵列天线，阵元的排列方式和阵元方向图通常是一定的，主要通过调整阵列的加权值得到期望方向图。

3 方法介绍

自适应阵列通过不同的性能准则确定阵列权向量的最优解，使阵列方向图在信号方向形成主瓣，同时在干扰方向形成零陷。自适应波束形成方法主要关注信号方向和干扰方向的阵列增益，对于主瓣形状和旁瓣形状的控制显得力所不及。在实际应用中，自适应权值并不能实时得到，当前计算的权值是前一段时间内的训练数量的结果。也就是说，自适应处理得出的权值只是在之前观察时间内的目标和干扰方向上形成的主瓣与零陷，当干扰或者目标处于高速运动状态下，实际目标与干扰方向并不在阵列方向图的主瓣与零陷位置，导致阵列天线的接收性能下降。

如果能够在自适应零点附近形成低电平，同时其他区域的旁瓣电平也尽可能低，这样既可以减小干扰方向变化带来的影响，又可以在一定程度上抵消其他方向的突发干扰。此外，对测控系统来说，目标空间运行范围广，要求阵列天线能够在宽角范围（甚至全空域）内保持对目标的跟踪、测量与控制。而扫描角的变化将导致阵列方向图指向、主瓣宽度以及增益等畸变，这种变化在平面阵中尤为明显[15]。虽然共形阵能够很好地解决平面阵中空间扫描角的不足，但是共形阵的特殊结构带来了制作工艺以及波束控制网络等方面的难题[16]。因此，有必要对阵列方向图主瓣特性进行控制，使其在不同空间指向上保持增益、主瓣宽度、指向精度与期望主瓣一致。鉴于自适应原理方向图综合法和优化理论方向图综合法的特点，首先由自适应原理方向图综合法得到能够抑制动态干扰的复杂旁瓣波形，并以此作为参考旁瓣，而后采用凸优化理论修正不同指向角带来的主瓣畸变，使最终方向图的主瓣特性与期望主瓣一致，旁瓣波形逼近于自适应原理方向图综合法得到的结果。

3.1 基于自适应原理的旁瓣赋形方法

天线阵列接收到的信号矢量除了期望信号以外，一般还包含干扰信号与噪声，因此阵列接收到的总信号为

其中，Xs为期望信号，Xu为无用信号，无用信号包括干扰信号Xj和噪声Xn。对方向图进行赋形的目的是寻找一组最优权值，使阵列天线的方向图在期望方向增益尽可能大，而干扰方向的增益尽量小，从而提高阵列输出的信号和干扰、噪声的功率比(SINR)。最大信噪比准则利用无用信号以及期望信号的自相关，求得最佳权值使阵列天线输出信噪比最大。若只期望在一个方向形成主瓣，最优权值表示为[17]

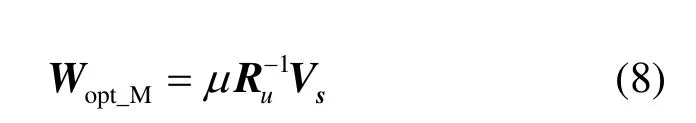
其中，µ为Ru-1Rs的最大特征值，Rs和Ru分别为期望信号和无用信号的自相关矩阵，Vs是目标方向的导向矢量。若令期望信号与噪声的振幅和导向矢量分别对应为As、Aj和Vs、Vj。则有

其中，H表示共轭转置，σ2为天线阵元的噪声功率。

根据自适应原理，阵列天线能够自适应地在干扰方向形成凹点，且干扰强度越大，凹陷越深。由这一启迪可在阵列天线的旁瓣区域引入大量人为干扰，最大信噪比准则会根据干扰功率的大小在各个干扰方向调整方向图包络的大小。方向图旁瓣包络较大的位置注入较大功率的干扰，在包络较小的位置则注入较小的干扰，通过不断地调整注入干扰的相对大小，最终使旁瓣方向图包络调整到设计大小。

在对阵列方向图旁瓣进行调整之前，需要确定期望旁瓣包络大小。以一维方位方向为例，设副瓣在θ方向的增益比主瓣峰值pmax低D(θ)dB，则期望电平为d(θ)=pmax/10(D(θ)/20)。为了使副瓣包络达到期望要求，需要不断调整每次注入的干扰大小。设第k+1次施加干扰强度为

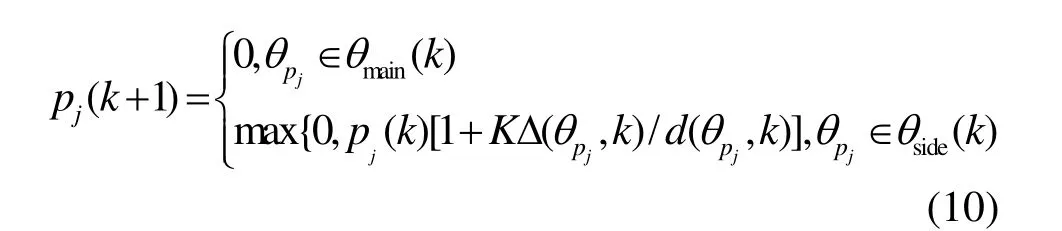
其中，K为调节系数，k为迭代增益，与文献[4]相比，式(10)通过修改迭代关系使k=1对大多数阵列都是收敛的。Δ(θpj,k)表示第k次迭代后θpj,处方向图电压p(θpj,k)与期望电压d(θpj,k)的偏差。Pj的初始值可以取1或者0。由天线的基本原理可知，随着旁瓣电平被不断压低，主瓣会被展宽，因此，在每次迭代时需要重新确定主瓣的范围θmain(k)。

以N=21的线阵为例，阵元间距不同且小于信号波长的一半，阵元坐标为[0, 0.39, 1.2, 1.7 2.1, 2.7,3.2, 3.5, 4.4, 4.6, 5.0, 5.4, 5.6, 6.5, 6.8, 7.3, 7.9, 8.3,8.8, 9.6,10.0]λ。信号方向为θs=0°，SNR=0 dB，干扰方向为θs=-30°，JNR=30 dB。利用式(6)与式(10)对阵列方向图进行综合，为了有效抑制干扰，在干扰方向形成较深零陷，干扰附近旁瓣电平要尽量低，同时在目标信号方向形成主瓣峰值。经自适应原理方法综合后的方向图如图1所示，对应方位角需要注入的干扰强度如图2所示。

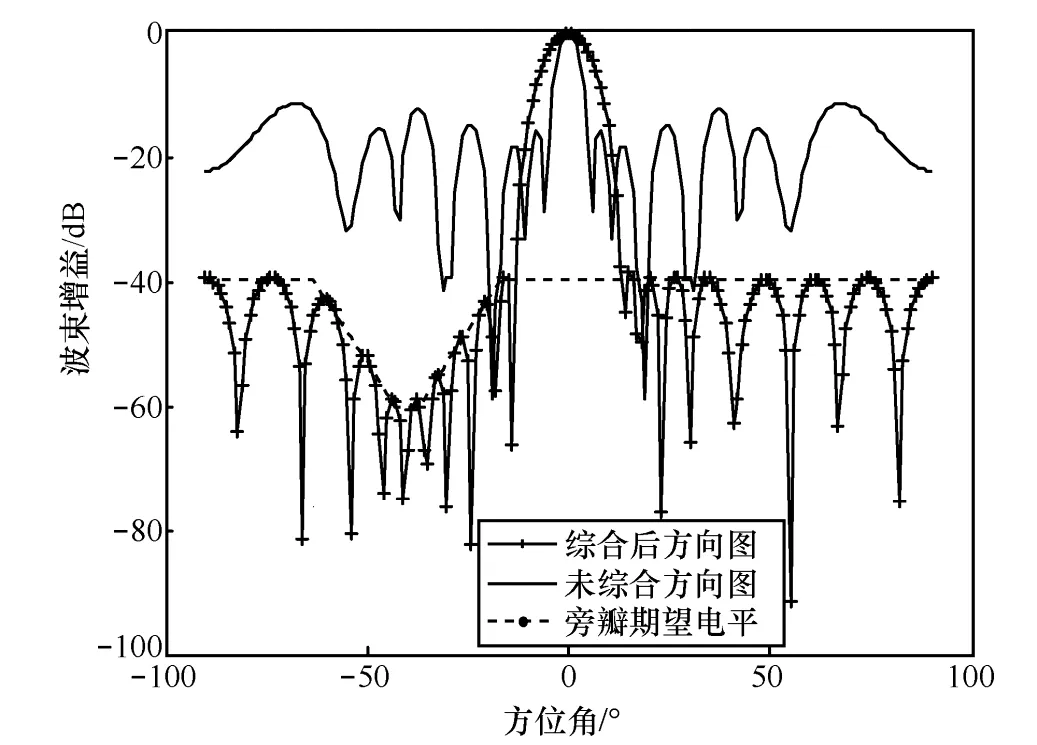
图1 自适应综合法得到的方向图

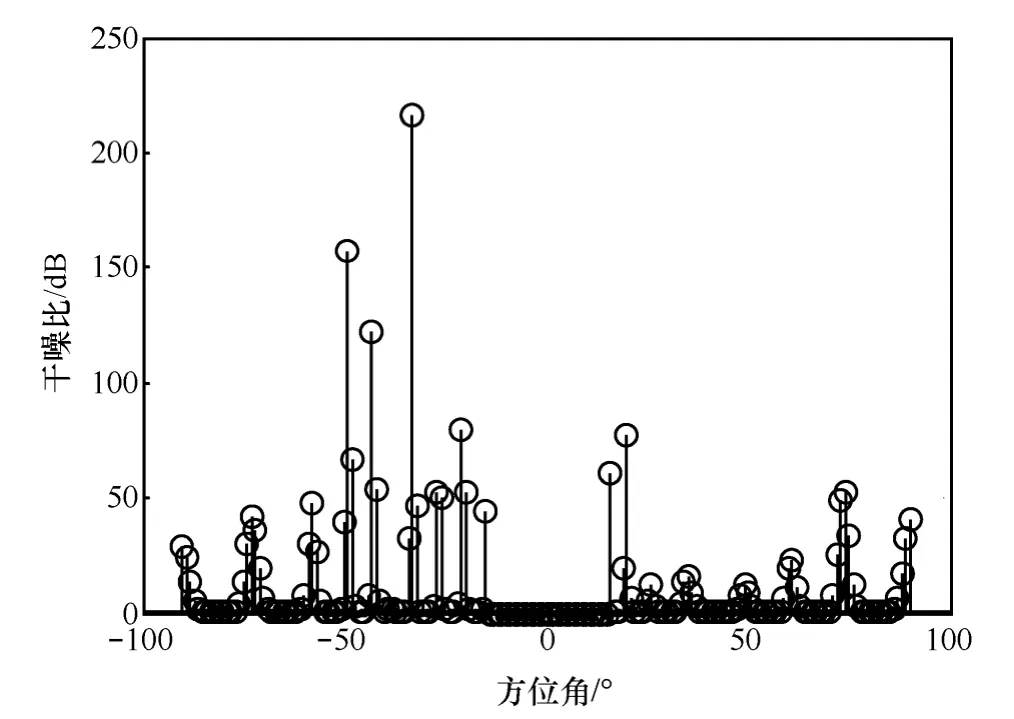
图2 各方位角上干扰强度

由图1可以看出，综合后方向图在干扰方向及其附近形成了凹陷，同时降低了整个旁瓣包络电平，但这些性能的获得是以主瓣被展宽为代价的。图2在零陷位置需要注入的干扰强度大，旁瓣电平变化相对较小的角度注入干扰较小，而主瓣区没有注入干扰，也就是说，这里只是对旁瓣进行了赋形，没有涉及到主瓣控制问题。

3.2 期望主瓣下的方向图综合

在实际中，不单单是旁瓣区域，天线波束的主瓣区域往往更加值得关注。因此，在天线的设计中常常会面临如何在一定的主瓣指向精度、增益稳定性以及主瓣宽度等情况下，使旁瓣电平最低的问题，这就涉及到期望主瓣响应波束形成。由于天线的主瓣宽度与主副瓣电平比是天线设计中不可避免的矛盾，不可能在获得极低的旁瓣电平的同时，主瓣宽度又能达到极窄。

因此，较为合理的期望主瓣响应方向图综合准则应为：在保证方向图旁瓣设计要求的条件下，让综合后主瓣响应与期望主瓣的误差达到最小，或者在满足设计方向图主瓣响应达到期望主瓣响应的要求下，使旁瓣最小化。期望主瓣响应与特殊形状旁瓣设计要求两者只能折中考虑。本文考虑在保证方向图满足期望主瓣响应的前提下，使综合后旁瓣与自适应方向图综合方法得到的结果最接近。

凸规划属于非线性规划的一种，其主要特点是规划的局部最优解即为全局最优解。作为凸规划问题的子集，二阶锥规划(SOCP, second-order cone programming）在满足二阶锥约束和线性约束的条件下，可使线性函数最小。随着处理锥优化问题工具箱的出现与发展[18]，求解二阶锥和线性约束下的凸优化问题变得十分方便，具有计算简单、精度高等优点。

不失一般性，考虑一维方向角方向。假设期望主瓣波束为pd(θ),θ∈[θmL,θmH]。为使阵列方向图满足主、旁瓣设计要求，最优权向量应是下列约束问题的解。

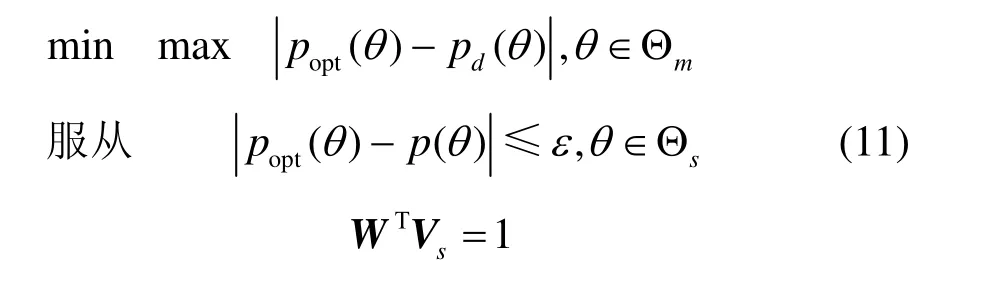
其中，Θm=[θmL,θmH]表示主瓣区，θmL和θmH为主瓣的临界角，Θs=[-0.5π,θmL)∪(θmL,0.5π]表示旁瓣区，p(θ)为k次迭代后得到的θ角处方向图电平，Vs为目标方向导向矢量，ε为一正实数，表示旁瓣误差电平。式(11)中期望波束响应不仅对幅度进行了约束，还约束了相位信息，导致式(11)的优化结果与阵列的参考点选取有关。应用中，更关心的是波束的幅度响应，而对相位响应并不做要求。在这种情况下，综合后得到的阵列方向图具有更高的幅度逼近精度。可将式(11)写成

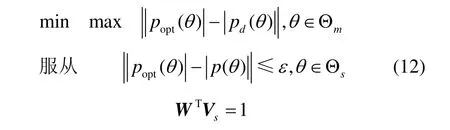
上式优化结果与相位无关，但目标函数已不再是凸函数，不能保证求得的局部最优解就是全局最优解。为此，可采用凸优化循环迭代的方法对该非凸问题进行求解，通过多次的二阶锥规划方法优化，直到得到满意的主瓣幅度响应方向图。

由于设计中只关注综合方向图的幅度响应，在初始迭代运算时，可通过选取恰当的主瓣相位响应再由式(11)求解阵列方向图，从而保证二阶锥优化结果为全局最优解。循环迭代过程如下。

1) 鉴于综合后得到的阵列方向图与相位无关，不妨选择期望主瓣相位响应为零相位。根据式(11)可以得到零相位时的最优加权向量Wr，此时的阵列波束方向图为pr(θ)=(Wr)Ta(θ)，a(θ)为阵列导向矢量。

2) 利用1)所得方向图pr(θ)的主瓣相位响应（记为∠pr(θ)，θ∈Θm）和期望主瓣响应pd(θ)的幅度∣pd(θ)∣，重新构造期望主瓣响应pdr(θ)=∣pd(θ)∣exp[j∠pr(θ)]，使新的期望主瓣响应为凸函数。由pdr与pd(θ)具有相同的幅度响应，pdr与pr(θ)具有相同的相位响应可得

3) 以新构造的期望主瓣响应pdr(θ)作为目标函数，运用式(11)凸规划的寻优方法，求得此时的最优加权向量Ws，对应的波束方向图为ps(θ)=(Ws)Ta(θ)。与pr(θ)相比，优化后的方向图ps(θ)更加逼近于pdr(θ)，即满足

经过上述一次迭代过程后，可以得到如下关系式

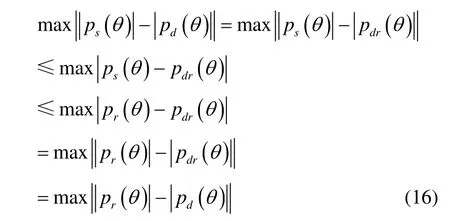
由上式易知，该迭代方法可使式(12)目标函数逐渐减小，因此该算法是收敛的，重复上述迭代过程，直到得到满足期望主瓣响应的阵列方向图。

4 仿真实验

实验 1指向角对自适应原理方向图综合法波束主瓣的影响。仿真模型同3.1节，目标角度分别取θs=0°、20°、35°、40°，其他参数不变，运用自适应原理阵列方向图综合法，得到自适应原理法综合后的方向图如图3所示。由图3可以看出，为了达到旁瓣电平的设计要求，牺牲了方向图的主瓣特性，主瓣被展宽，主瓣峰值指向偏离目标角，且随指向角的增加，主瓣畸变严重程度也增加。

实验 2期望主瓣下阵列方向图综合。由实验1可知，自适应原理方向图综合法得到主瓣波束易随波束指向的变化而产生畸变。为了使综合后方向图能够在不同空间指向上，保持所需的主、旁瓣特性，采用本文所述方向图综合方法，在阵列方向图综合之前确定期望主瓣，而后在此期望主瓣响应下，通过循环迭代方法保证方向图在满足期望主瓣响应的同时，保证综合后旁瓣逼近于自适应方向图综合方法得到结果。

假设以0°指向角的方向图主瓣作为期望主瓣，主瓣宽度为 20°。由于自适应原理综合法只是对旁瓣进行了赋形，这里选择凸优化方法产生期望主瓣，所得期望主瓣如图4所示。

图4 期望主瓣响应方向图

可见，在期望主瓣条件下，阵列一致旁瓣电平最低可达-35 dB，且在干扰方向形成凹陷，但凹陷深度较浅。运用二阶锥规划方法得到的期望主瓣方向图，还可为自适应原理综合方法中期望旁瓣电平的选取提供参考。

在图4所示的期望主瓣响应下，当阵列方向图主瓣指向 20°、40°、-20°时，与之对应的干扰方向为-30°、-30°、35°，结合式(10)与式(12)阵列方向图综合方法，得到不同主瓣指向的方向图如图5所示。

图5 期望主瓣下不同指向阵列方向图综合效果

由图5可以看出，通过对主瓣宽度和主瓣峰值指向的约束，使不同空间指向的综合后阵列方向图能够保持良好的主瓣特性，有效减小了宽指向角带来的主瓣畸变。同时，综合后方向图具有与自适应综合法所得的方向图一致的旁瓣特性，且在干扰方向形成零陷，其附近区域旁瓣电平包络也与设计电平基本一致。

实验 3循环迭代次数对阵列方向图综合的影响。由3.2节分析可知，为实现对非凸问题(式(12))的求解，采用了对凸优化问题(式(11))的循环迭代运算，而迭代运算次数的不同直接影响综合后阵列方向图与期望主瓣的一致程度。以目标方向θs=30°、干扰方向θj=-25°为例，其他参数同前文，图 6(a)为不同循环迭代次数γ时的阵列综合方向图，图 6(b)为主瓣宽度与最大旁瓣电平随迭代次数的变化关系。

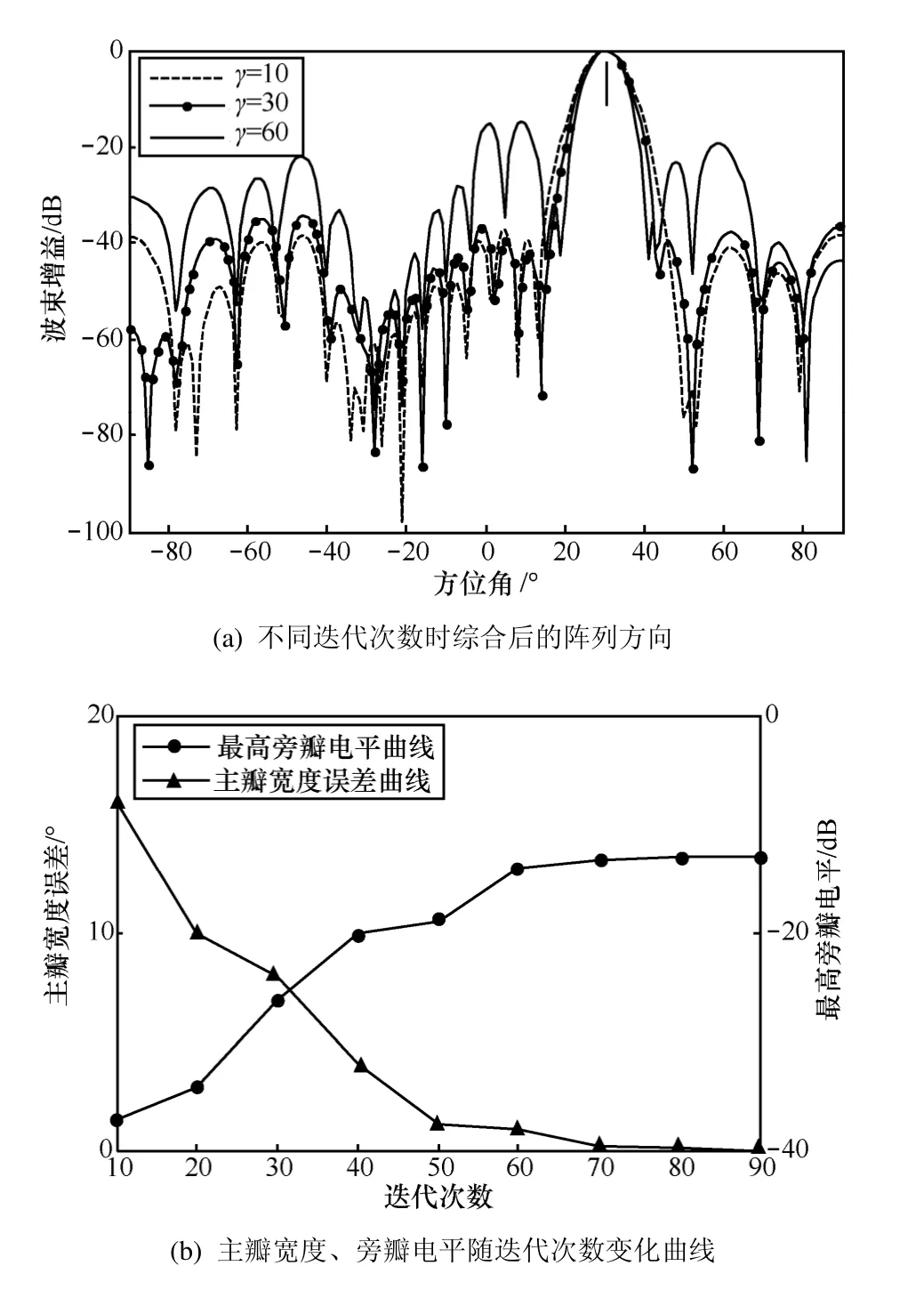
图6 迭代次数对阵列方向图综合的影响

循环迭代次数越大，综合后方向图主瓣与期望主瓣误差越小，但是过多的循环运算不但会降低算法运算速度，还将导致方向图旁瓣电平被抬高。一般情况下，可选择满足期望主瓣要求下的最小循环迭代次数。

5 结束语

结合自适应原理方向图综合法与优化理论方向图综合法的特点，运用两者混合算法实现对任意阵列的方向图综合，并就循环迭代次数对混合算法的影响进行了分析。为减小不同目标角指向对方向图主瓣的影响，通过期望主瓣响应对阵列方向图进行约束，使综合后的方向图在不同指向上与主瓣和期望主瓣一致。当然，实际应用中，要求测控天线扫描角的范围很广，甚至要求全空域内对目标保持持续的跟踪与控制。仅仅依靠阵列方向图综合方法很难满足上述需求，还需要对阵元分布进行优化，将方向图综合方法与共形阵相结合，才能实现真正意义上的全空域阵列天线。此外，本文方向图综合方法在求解非凸优化问题时，需要一定次数的迭代运算才能到达期望主瓣响应的要求，这也限制了算法在高实时性要求下的应用。

[1] TSENG C Y, GRIFFITHS L J. A simple algorithm to achieve desired patterns for arbitrary arrays[J]. IEEE Transactions on Signal Processing, 1992, 40(11):2737-2746.

[2] WU L, ZIELINSKI A. Equivalent linear array approach to array pattern synthesis[J]. IEEE Journal of Oceanic Engineering, 1993, 18(1): 6-14.

[3] DUFORT E C. Pattern synthesis based on adaptive array theory[J].IEEE Transactions on Antennas and Propagation, 1989, 37(8):1011-1018.

[4] OLEN C A, COMPTON R T. A numerical pattern synthesis algorithm for arrays[J]. IEEE Transactions on Antennas and Propagation, 1990,38(10):1666-1676.

[5] ZHOU P Y, INGRAM M A. Pattern synthesis for arbitrary arrays using an adaptive array method[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(11):1759-1760.

[6] LEBRET H, BOYD S. Antenna array pattern synthesis via convex optimization[J]. IEEE Transactions on Signal Processing, 1997,45(3):526-532.

[7] TSUI K M, CHAN S C. Pattern synthesis of narrowband conformal arrays using iterative second-order cone programming[J]. IEEE Transactions on Antenna and Propagation, 2010, 58(6):1959-1970.

[8] YAN S F, MA Y L, YANG K D. Optimal array pattern synthesis with desired magnitude response[J]. Sonar Detection Systems I, 2004,14(11):510-522.

[9] 赵光辉, 陈伯孝. 基于二次编码的 MIMO雷达阵列稀布与天线综合[J]. 系统工程与电子技术, 2008, 30(6):1032-1036.ZHAO G H, CHEN B X. Pattern synthesis of antenna array in MIMO radar by using two-layer coding[J]. System Engineering and Electronics, 2008, 30(6):1032-1036.

[10] FRANCISCO J, ARES P. Genetic algorithm in the design and optimization of antenna array pattern[J]. IEEE Transactions on Antenna and Propagation, 1999, 47(3):506-510.

[11] ZHAO F, XIAO K, QI H,et al. Preconditioned alternate projections method to synthesise conformal array[J]. Electronics Letters, 2011,47(13):735-736.

[12] GUO Q, LIAO G, WU Y,et al. Pattern synthesis method for arbitrary arrays based on LCMV criterion[J]. Electronics Letters, 2003, 39(23):1629-1630.

[13] BENJAMIN F, JEAN J F. Optimal narrow beam low sidelobe synthesis for arbitrary arrays[J]. IEEE Transactions on Antennas and Propagation. 2010, 58(6): 2130-2135.

[14] 赵菲, 赵会颖, 邱磊等. 自适应动态 Meta粒子群优化算法综合多方向图共形阵列[J]. 电子与信息学报, 2012, 34(6):1476-1482.ZHAO F, ZHAO H Y, QIU L,et al. Adaptive dynamic Meta particle swarm optimization algorithm synthesizing multiple-pattern conformal array[J]. Journal of Electronics & Information Technology, 2012,34(6):1476-1482.

[15] TREES H L. Optimum Array Processing Part IV: Detection, Estimation and Modulation Theory[M]. New York, USA, John Wiley & Sons Inc, 2002.

[16] TOMASIC B, TURTLE J, SHIANG L,et al. The geodesic dome phased array antenna for satellite control and communication-subarray design, development and demonstration[A]. IEEE International Symposium on Phased Array Systems and Technology[C]. Hanscom AFB,MA, USA, 2003.

[17] ZHOU P Y, INGRAM M A. Pattern synthesis for arbitrary array using an adaptive array method[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(5):862-869.

[18] STURM J F. Using SeDuMi 1.02, a matlab toolbox for optimization over symmetric cones[J]. Optimization Methods and Software, 1999,11(12):625-653.