基于局部横向强度要求的船舶侧向承载板厚度设计研究
2014-01-01邱伟强
孙 利,邱伟强
(中国船舶及海洋工程设计研究院,上海 200011)
0 引 言
随着结构力学理论的发展与计算机技术的进步,以及对于满足强度要求的前提下最大限度减轻空船结构重量的追求,人们不再满足于基于线弹性理论进行结构设计,而是追求更为经济的基于非线性塑性强度的结构设计。对于承受侧向载荷作用的板厚计算问题,也早已成为非线性塑性设计的研究焦点之一。发展至今,主要有两类比较成熟的解析方法用于钢制板材极限强度的计算,分别是:弹塑性理论法(elastic-plastic theoretical solution)和刚塑性理论法(the rigid-plastic theoretical solution)。这两种方法确定了塑性设计极限强度的上下界,巧妙地将平衡方程与机构运动进行解耦,降低了求解结构塑性问题的难度[1]。
弹塑性理论法假设结构材料为理想弹塑性材料,通过求解板的弯曲微分方程得到承载板系统的应力分布,并引入塑性弯矩和塑性铰的概念以确定板的崩溃载荷。Paik[2]介绍的膜应力法(the membrane stress method)与弹塑性理论法的思路类似,它是通过求解基于大挠度理论的板的非线性弯曲微分方程得到板内膜应力,该方法认为当膜应力达到某一屈服准则的许用值时板达到极限状态。
刚塑性理论法假设结构材料为刚塑性,忽略弹性阶段。它首先假定板破坏时的结构形式,然后应用能量法建立应变能与外力做功相等的方程,从而得到最小能量所对应的极限载荷[3]。对于受侧向载荷板的极限强度问题应用刚塑性理论法的研究可以参考文献[4]和文献[5]。
CSR(油船与散货船共同规范)关于受侧向载荷作用的板其厚度设计给出了类似的最小厚度约束公式,公式是以长宽比无限大时板条梁的极限强度作为设计基础,再乘以有限长宽比系数予以修正。然而通过对比发现两本规范所给出的板的长宽比系数的计算公式不尽相同,当长宽比≤2.5时尤为明显[6,7]。油船的强框架间距一般比散货船底部强度间距要大,一般情况下均>4甚至>6,因此应用两种长宽比系数计算公式结果差别不大。然而,对于散货船而言,一般底部区域的板格的长宽比要小很多,应用两种不同公式可能带来板厚要求>10%的差别。从控制空船结构重量的角度来说,即使是0.5mm的差别对于整体结构重量的影响相当可观。此外,随着HCSR(协调共同规范)的面世,两类长宽比系数计算公式也将统一,因此,深度探究两种公式中哪种更为经济和准确具有重要的研究价值。
参考前人的理论研究成果,结合非线性有限元软件进行数值计算分析,论证了一个更为经济准确的侧向承载板的板厚理论设计公式,进而佐证了散货船公式相较油船共同规范所给公式在保证安全的前提下更为经济优化。
1 板的极限强度影响因素
加筋板格是船体板架结构的基本组成元素,如何合理地将整体板架中单一板格内的板作为独立的研究对象进行分析,对于侧向承载板极限强度计算的准确性有着至关重要的影响。
1.1 边界条件
将板格四周边界处的约束条件理想化为4种情况,在这4种情况下,板边界均提供垂直于板面方向位移约束[8]:
1) 简支——板边可以自由转动且可以在板面内自由移动;
2) 铰支——板边可以自由转动,但不可在面内自由移动;
3) 移动自由的嵌固——板边不可自由转动,但可以在板面内自由移动;
4) 刚性嵌固——板边不可自由转动或在板面内自由移动。
边界条件“2)”和“4)”的面内移动(即不存在板边“趋近”)只能发生于支承板的结构在此方向刚性非常大的情况中。这一约束终究须由整个加筋板格边缘处的骨架产生,而梁的弯曲刚度一般不足以提供这样的刚性面内支撑,该种假设会使结果偏于危险。而边界条件“1)”和“3)”一般较为保守。当载荷作用于单一板格时,边界条件“1)”和“2)”是合适的,因为无论扶强材或是周围板格都不能提供足够强大的转动约束;而当分布压力载荷遍布于若干板格时,由于对称性将提高边界处的扭转约束,所以边界条件“3)”和“4)”是合适的。而船体板架一般都有若干板格承载侧向载荷,所以综上所述,应用边界条件“3)”对本研究对象较适合。
为了验证上述假设,研究了一系列长宽比不同的板格,对比了单一独立板格在边界条件“3)”约束下的板格极限强度与以5个连续加筋板格为统一研究整体的板格极限强度。对于后者取5个板格的中间一个的计算结果。由于连续板的极限强度与加强筋的尺寸有很大关系,选取4种在实际设计中较为常见的结构尺寸作为研究对象,具体研究模型尺寸见表1。

表1 4种研究模型尺寸 单位:mm
总体模型的边界条件也为移动自由的嵌固。单元的尺寸为50mm×50mm,加强筋以梁单元考虑截面偏心的方法模拟。
应用 Abaqus非线性有限元软件进行计算,考虑结构大变形的几何非线性与材料非线性问题,材料性质设置为理想弹塑性。
根据计算结果,对于“3”和“4”两种情况,单一板格与连续板格中点处位移与侧向载荷p的关系曲线见图1、2。

图1 计算模型“3”载荷位移曲线

图2 计算模型“4”载荷位移曲线
从图1和图2可知,移动自由的嵌固这一理想边界条件由于忽略了中面力的影响,依据该边界条件得到的计算结果与考虑加强筋所提供的面内支持作用所得到的结果相比,前者计算得到的板的极限强度较低,因此采用边界条件“3)”对于侧向承载板的板厚设计是偏于安全的。对于工况“4”,本文加算了考虑边界条件“4)”时单一板格的载荷位移曲线,从图 2可知,应用边界“4)”时仅出现了一个折点,即两长边出现塑性铰,然后由于中面力的作用板格的承载力一直上升,中间位置塑性铰在所设定的载荷范围内没有出现,从而可知应用边界“4)”必将导致得到的偏于危险的结果。此外,对比两种长宽比的板格计算结果可以看出随着长宽比l/s的增加,基于边界条件“3)”得到的板的极限强度与考虑加强筋支持的连续板的极限强度结果差距逐渐减小,这与薄膜效应中的几何相容性约束随着长宽比的增长而逐渐减弱有关。
而对于计算模型“1”和“2”,由于这两种模型下的板的长宽比较小,几何相容性约束较为突出,单一板格在没有四周面内支持下,由于几何相容性条件的影响,板将在对角线位置形成塑性铰,而不是像“3”、“4”一样在板宽中间位置形成。因此,“1”、“2”情况下,单一板格在理想边界条件下,载荷位移曲线没有出现明显的拐点,所以不能应用形成铰机构作为评判板达到极限强度的依据。而连续板情况,由于加强筋提供了一定的面内支持,保证了板的塑性铰分布与“3”、“4”相类似,所以载荷位移曲线会出现明显的拐点,见图3、4。
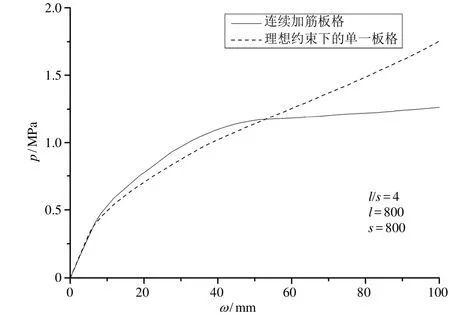
图3 计算模型“1”载荷位移曲线
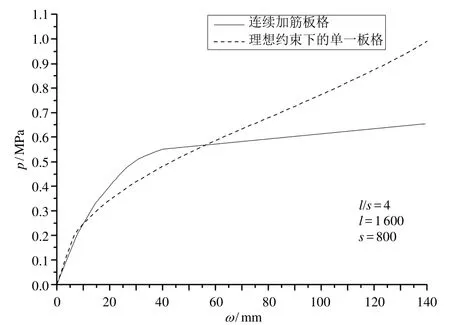
图4 计算模型“2”载荷位移曲线
虽然长宽比较小时,考虑大挠度的几何非线性情况下,在边界条件“3)”下无法准确找出板的载荷位移曲线的明显拐点,通过图 3、4可知,即使是考虑了加强筋的面内支持作用,曲线出现拐点时所对应的位移已经远远超过板自身的厚度,此时的结构设计不应仅局限于满足强度衡准,而应该基于永久变形小于某许用值作为依据。而研究计算模型“3”和“4”的结果可以知道,移动自由的嵌固这一理想边界条件可以给出较为准确且安全的计算结果,尤其是当板的长宽比较大时该边界条件可提供的准确性更高。
对于纵骨架式板格而言,短边的边界强度要高于长边,即相对于长边短边处平面内线位移更小。然而,为了保守考虑,这里两种边界的线位移均放开,以减小薄膜效应的影响。
当然,正如文献[2]所提到的,板上的加强筋的强度衡准在设计时往往要高于板的强度衡准,因此,对于连续的板架结构来说,在板局部破坏之前,加强筋应始终保持平直,故建议在上述边界条件“1)”与边界条件“3)”的基础上,添加保持边界上节点面内位移平直共线的约束。增加如此约束后,板内由于几何协调性作用产生面内应力,在一定程度上承担板所受的侧向载荷,从而增强了板的极限承载力。但此假设未曾虑及侧向承载板为普通钢而加强筋为大跨度高强度钢材质的情况,因此以安全性为基本要求的结构设计来说,应该忽略这一约束的影响。
总之,基于以上研究计算与分析,对于受侧向载荷作用的板的极限强度计算问题,应采用边界条件“3)”作为有限元模型计算板格四周的边界条件。
1.2 大挠度理论与薄膜效应
很多情况下应用小挠度理论设计侧向承载板会使板设计过厚。这是因为小挠度理论未考虑当挠度变大以及板边被阻止趋近时所产生的薄膜应力。文献[9]中给出了受均匀水压作用的刚固约束矩形板在中心处位移与水压大小的关系曲线(见图 5)。通过该实验可知随着水压的增加,矩形板首先在四周边界处形成塑性铰,然后在板中心处形成塑性铰,然而此时尚未达到板的屈服极限,板中心处的位移没有剧烈增大而是板膜应力迅速增大,最后整个板大面积屈服直至变成塑性膜,板中心的位移增量与载荷增量几乎成正比。从而也证明了膜应力对于增加板极限载荷的作用。
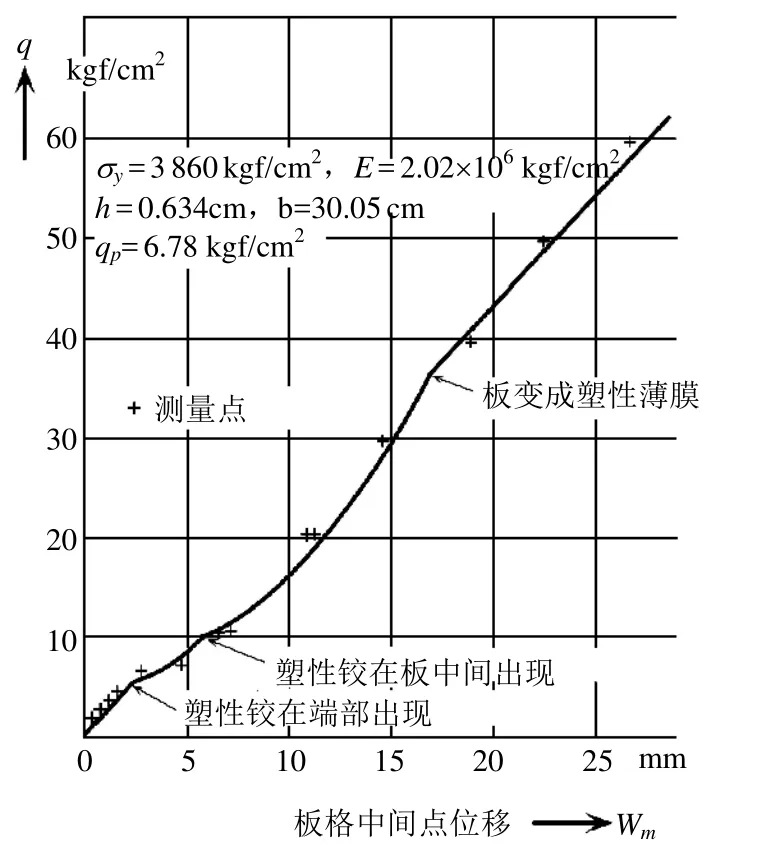
图5 刚固约束的矩形板在均匀水压作用下板中心挠度与载荷关系曲线
根据文献[8],如果板边被阻止趋近,则当侧向挠度(包括初始挠度以及受侧向载荷引起的挠度)ω>t/2时,薄膜效应变得显著,当ω>1.5t时大部分侧向载荷将由薄膜拉伸而不是由板的弯曲支持;如果板边可以自由趋近则薄膜应力一般要推迟到挠度ω>t才变得显著,仅有的薄膜效应是由于几何相容条件引起的面内应变(中央部分受拉,板边周围受压)。此外,长宽比较大的板根本不会产生薄膜效应,因为筒形挠曲形状是可展曲面,必定满足几何相容条件。
根据以上分析可知,板的边界条件是“移动自由的嵌固”约束条件,即允许板边在面内自由移动,仅对边界处挠度与绕板边的转动位移进行约束。因此,对于板边可以自由趋近;当板格长宽比较大时,板的薄膜效应影响很小;当板格长宽比较小时,由于几何相容条件引起面内应变,此时薄膜效应较严重。
为了验证以上理论并研究小板格长宽比对于薄膜效应的影响程度,针对两块长宽比不同的板,以“移动自由的嵌固”作为边界条件,加载侧向载荷,应用有限元计算法在大挠度与小挠度理论前提下,分别对其进行极限强度分析。对比图6、7可以发现,当板格长宽比l/s较大时,应用大挠度理论与否,对于受侧向载荷作用的板的极限载荷点的影响并不大,而对于板格长宽比等于1的极限情况来说,应用大挠度理论可以显著增加板的极限承载能力。主要原因是当l/s=1时,应用大挠度理论与小挠度理论求得的板的塑性应变分布是不同的,由于几何相容条件引起面内应变,薄膜效应导致除板边形成塑性铰外,不是先在板的中心处而是先在板格的对角线上形成塑性铰;相比而言,当板格长宽比l/s=5时,无论应用大挠度理论或是小挠度理论,除了在板边首先形成塑性铰之外,均在沿长边方向的板面中间线形成塑性铰,可以说几何相容条件对此种长宽比的板格应力应变分布的影响不大。
综上所述,为了对于各类长宽比的板格极限强度计算采取统一假设,这里不考虑大挠度引起的薄膜效应,因为虽然在长宽比较小的情况下薄膜效应比较显著,然而引入薄膜效应也只会增加板的极限承载能力,如此假设是偏安全的。
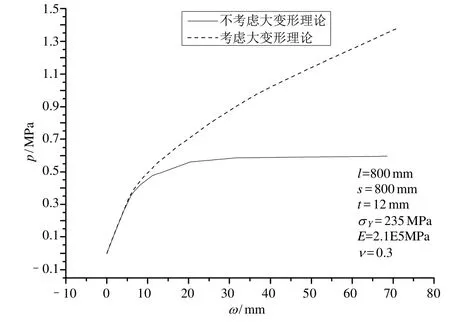
图6 长宽比l/s=1时,应用大挠度理论与否对于受侧向载荷板的极限强度的影响

图7 长宽比l/s=5时,应用大挠度理论与否对于受侧向载荷板的极限强度的影响
2 受侧向载荷作用的板的极限强度计算
2.1 基于刚塑性理论与弹塑性理论的受侧向载荷的板的极限强度计算
Wood[4]和Jones[10]提出了静压力载荷作用下,简支约束与刚固约束下板的极限强度的上下限公式:
简支约束:
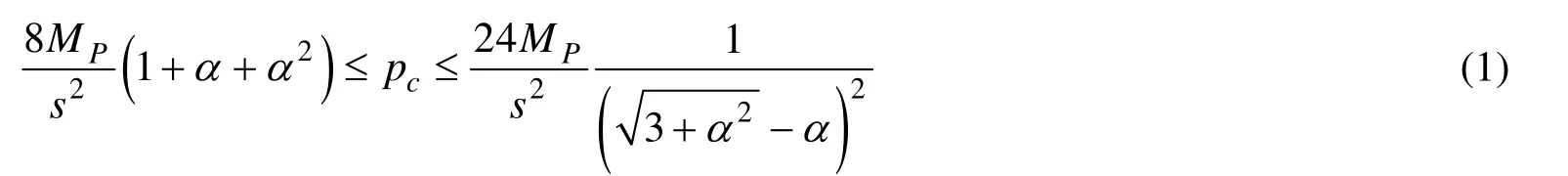
刚固约束:
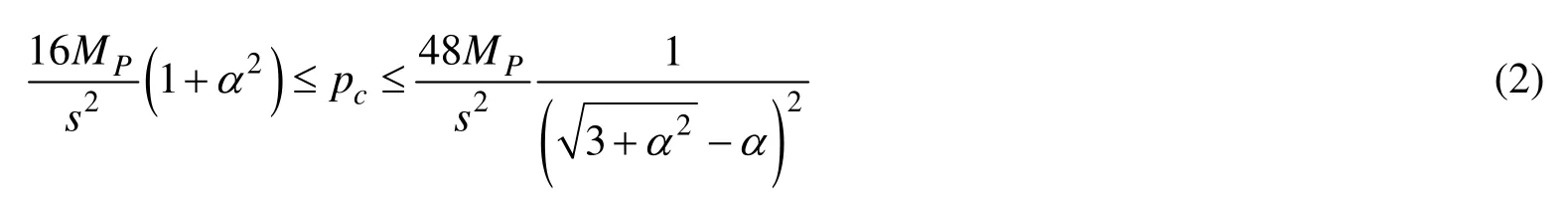
式(1)和式(2)中:α=s/l——表征板格的宽长比,其中l为矩形板长边长度,s为矩形板短边长度。MP——塑性弯矩:

式(3)中:t——梁的截面高度即板的厚度;(σx)Y——材料的屈服时板格短边方向的正应力。
2.2 数值计算结果与分析
为了验证两种理论以及CSR 所给公式的准确性和经济性,应用非线性有限元计算软件Abaqus对一系列受侧向载荷作用的板进行极限强度分析。
2.2.1 模型
根据以上理论分析以及规范给出的公式可知,板的极限载荷均与板的长宽比有关,选用常见的板格宽度s=800mm作为板宽,板厚t=12mm,仅变动板的长度l,模型其他具体参数如下:
(1) 网格大小:单元形状均为正四边形,网格尺寸接近板厚,取10mm;
(2) 材料属性:假定材料为理想弹塑性,屈服应力σY=235 MPa ,弹性模量E=2.1× 105MPa,弹性阶段泊松比v=0.3;
(3) 边界条件:取“移动自由的嵌固”为边界条件。为限制刚体位移,对两长边中点限制X方向位移,对两短边中点限制Y方向位移;
(4) 大挠度理论:基于安全性的考虑,不启用大挠度理论计算功能,仅应用小挠度理论求解。
2.2.2 计算结果
应用Abaqus有限元软件,得到板中点挠度ω随载荷p变化的关系曲线,通过观察曲线斜率的变化找出板中央区域形成塑性铰所对应的极限载荷pult。总结各类经验公式与规范,可以知道受侧向载荷作用的板的极限载荷为:

式(4)中:γ——与板格宽长比α有关的系数;MP——塑性弯矩,参见式(3)。在本例中:

计算结果见表2。
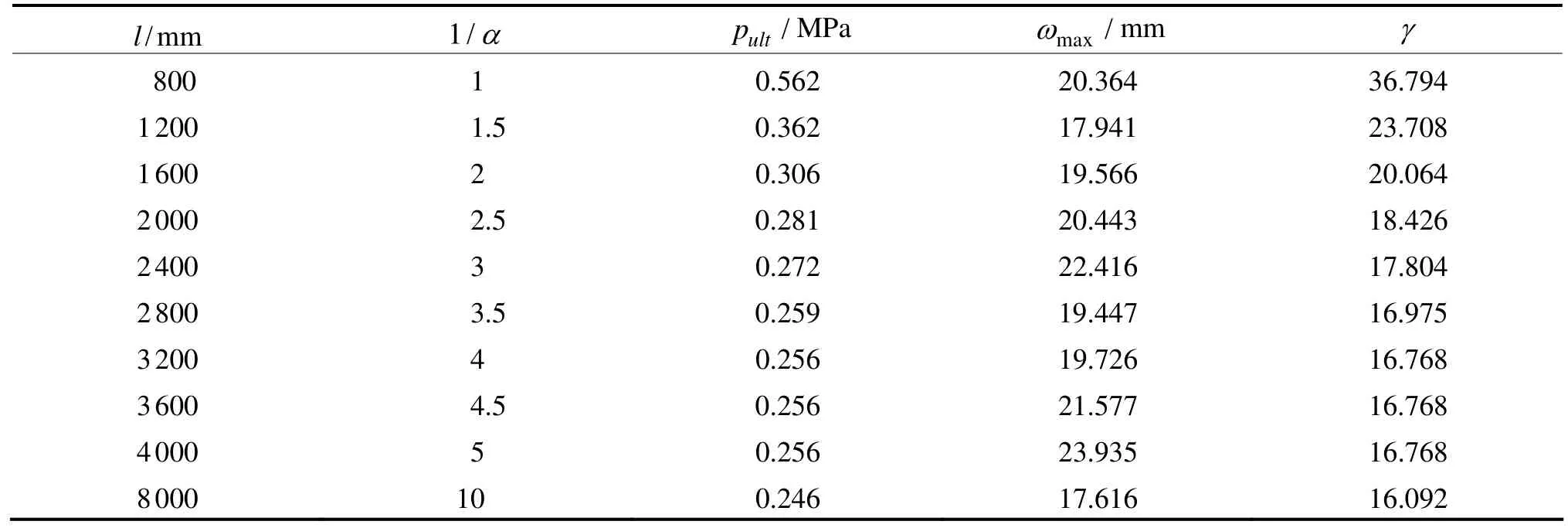
表2 s=800mm,t=12mm时,板的极限载荷随板长度l变化结果
对比式(4)的结构,基于刚塑性理论与弹塑性理论板的极限强度公式可转换为:

对比以上各种公式给出的γ随板的长宽比(即宽长比的倒数1/α)变化的关系式,见图8。
通过对比数值计算结果与理论推导给出的公式可知,基于弹塑性理论所给出的γ值与应用非线性有限元方法计算得到的结果最接近,在某特定宽长比α下,有:

通过对边界条件与薄膜效应的分析可知,采用所取的假设条件,计算得到的板的极限强度将偏安全,因此,从图8可知,根据弹塑性理论方法得到的板的极限强度公式足以满足塑性设计需要。而两类共同规范所给出的经验公式结果在不考虑其他因素(如焊接、钢材缺陷等)时也偏于保守。
综上所述,使用弹塑性理论在小挠度下计算得到经验公式来计算受局部横向强度要求的板的最小厚度要求,即:
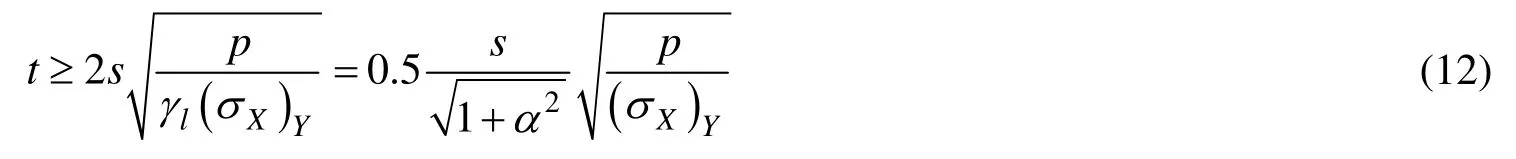
为了与共同规范公式统一,则式(12)变为:
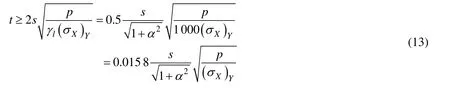
式(13)中:(σX)Y的取值还应当考虑总纵弯曲应力的影响,该问题可以参考文献[6]、[7]关于侧向承载板板厚设计公式的处理方法即折减板格许用应力的处理方式。
观察图9,对比该公式与两共同规范所给的板厚设计公式:(其中,t_oil,t_bulk和t_new分别表示在同一外部压强p和板材属性条件下应用油船共同规范、散货船共同规范以及本文所提出的公式得到的板的最小厚度)。
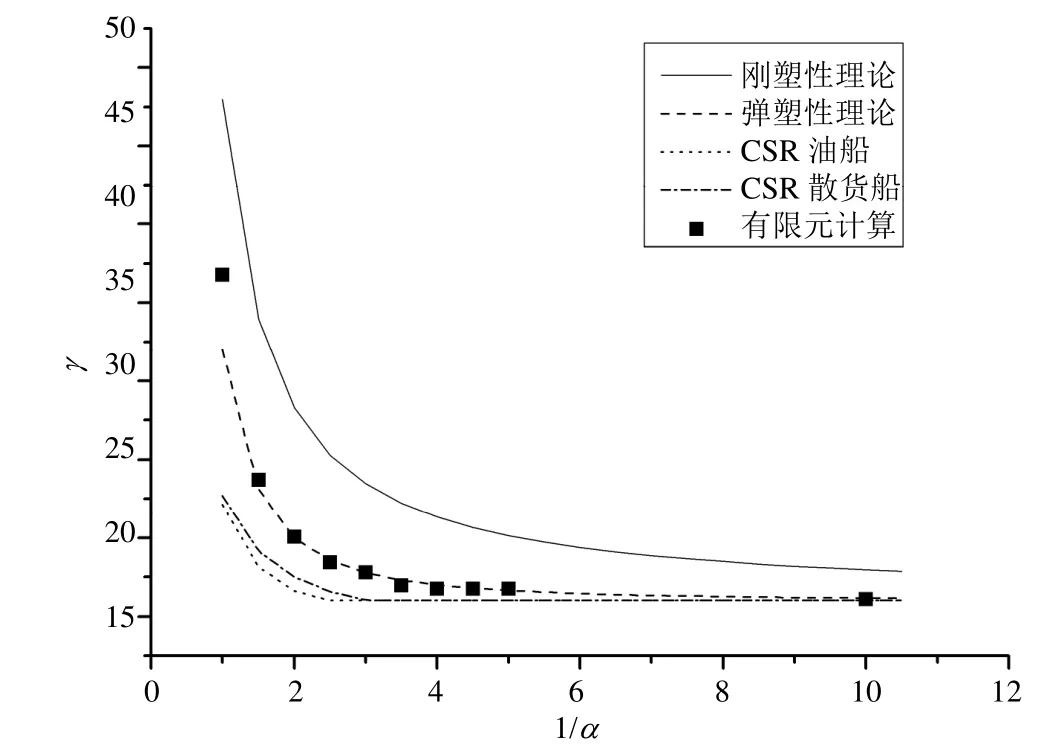
图8 各类计算方法给出γ与1/α的关系曲线
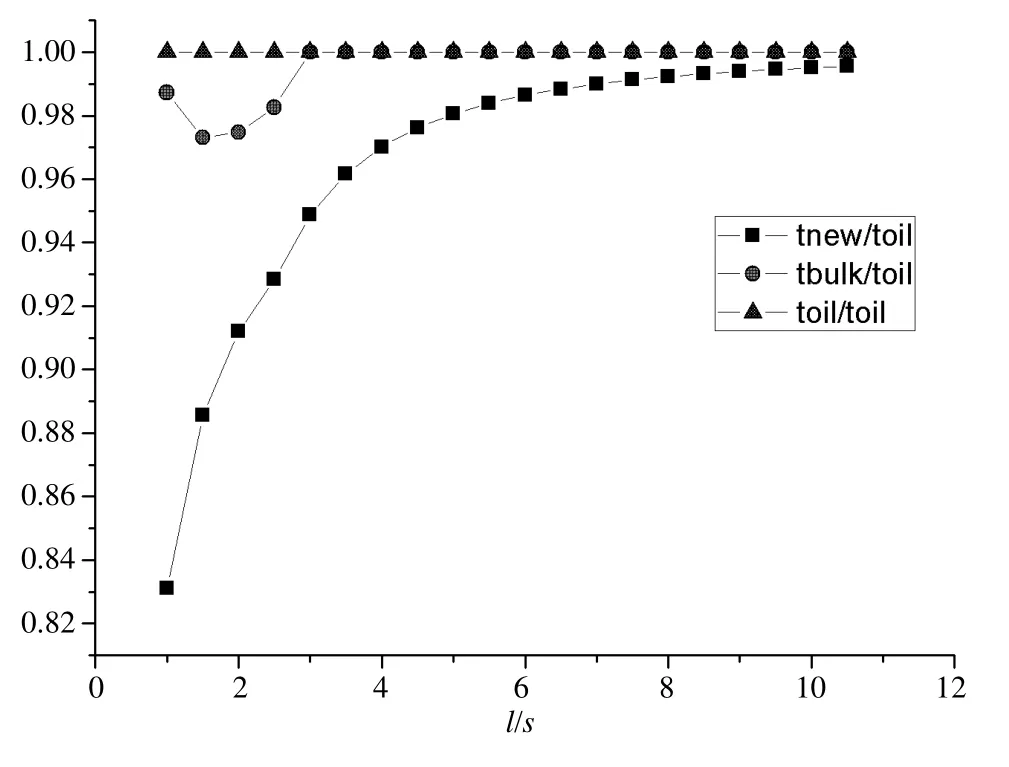
图9 不同板厚公式随边长比变化曲线
由图9可知,当板格长宽比系数小于3时,油船与散货船规范基本一致,系数大于3时,差别最多有5%,假设一块10mm的板格,应用不同规范可能有0.5mm的区别,这对于优化结构重量有重大影响。当长宽比小于4时,最小板厚趋势与散货船规范所给公式相似,但更为经济;当长宽比大于4时趋势与两规范相似,差别不大。
通过系统分析(包括边界假设、大挠度理论和薄膜效应等)以及国外学者所做相关实验研究[9]可知,所提供的板厚计算公式出于保守假设,所得受侧向载荷作用下的最小板厚设计公式是偏于安全的。需要承认,规范在制定时考虑的因素远多于理论分析(还有建造工艺、板材的初始变形等),与散货船共同规范所给公式的趋势相似,且更偏安全。在HCSR的相应章节中更为审慎的考虑散货船公式和油船公式取舍,在保证船舶安全的前提下使设计更为经济优化。
3 结 语
首先对可能影响船上侧向承载板的极限强度计算的几种主要因素(包括边界条件的选取、大挠度问题以及薄膜效应)予以了计算与研究,并选出了适合船体板实际情况偏保守的处理方式。为了选出更准确且经济的基于局部横向极限强度要求的板厚计算公式,采用非线性有限元软件Abaqus,经详细讨论的边界条件与其他假设,对一系列长宽比板格的板的极限强度进行计算,并将结果与CSR给出的经验公式、与基于刚塑性和弹塑性理论方法给出的计算公式相比较,最终结论为应用弹塑性理论方法给出的侧向承载板的极限强度计算公式最经济准确,并且该公式由于忽略了薄膜效应等因素,所得结果是偏于安全的。因此,建议选择本文提出的HCSR的侧向承载板的板厚计算公式。
[1] Jones, N.. Review of the Plastic Behavior of Beams and Plates. International Shipbuilding Progress [J]. 1972, 19(218):313-327.
[2] Paik, J.K. and A.K. Thayambailli. Ultimate Limit State Design of Steel-plated Structures [M]. 2003: Wiley.
[3] Murray, N.W.. Introduction to the Theory of Thin-walled Structures [M]. 1984, Oxford: Clarendon Press.
[4] Wood, R.H.. Plastic and Elastic Design of Slabs and Plates [M]. 1961, New York: The Ronald Press.
[5] Jones, N.. Structural Impact [M]. 1989, Cambridge: Cambridge University Press.
[6] IACS, Common Structural Rules for Bulk Carriers [M]. 2012.
[7] IACS, Common Structural Rules for Double Hull Oil Tankers [M]. 2012.
[8] Hughes, O.F.. Ship Structural Design: a Rationally-based, Computer-aided, Optimization Approach [M]. 1983, New York: Wiley.
[9] Okumoto, Y.. Design of Ship Hull Structures [M]. 2009: Springer.
[10] Jones, N., Plastic Behavior of Beams and Plates, in Ship Structural Design Concepts [M]. 1975, Cornell Maritime Press:Cambridge. 747-778.
