基于遗传算法的船舶螺旋桨优化设计

吴小平，刘洋浩，张 磊

（上海船舶研究设计院，上海 201203）

0 引 言

目前，船舶螺旋桨设计方法主要分为理论法和图谱法。动量矩理论、升力线法、升力面法、边界元法、雷诺平均N-S方程（RANSE）法[1,2]等均属于理论法。图谱法凭借其简单、实用的优势，目前仍被广泛应用。常用的螺旋桨设计图谱有日本的AU（MAU）系列、瑞典的SSPA系列以及荷兰的B系列，其中以B系列的资料最齐全，应用最广泛。

螺旋桨设计过程中涉及的参数多，采用传统的手工计算和查核图谱，最终可以设计出符合条件的螺旋桨。但是，设计过程中要针对不同的方案进行评判，在多张图谱中多次插值，是一项费时费力的工作。文献[3]将B系列图谱回归成多项式，通过多项式可以得到图谱范围内任意螺旋桨的敞水数据，减轻了查图谱的工作量。文献[4]采用Newton插值法代替传统的手工查图谱法，其设计结果与手工法相比接近。文献[5]提出了一种新的图谱设计法，该法以B系列4叶桨为例，将螺旋桨设计简化为单变量优化过程，可减少查图谱带来的误差。螺旋桨设计通常以效率（航速）作为目标函数，作为多变量、多约束优化问题，其目标函数与设计变量之间没有明显的数学表达式。遗传算法作为一种高效、并行、基于适应度函数的搜索法，非常适合求解这类问题。

1 遗传算法

遗传算法（Genetic Algorithm，GA）是一类借鉴自然界中优胜劣汰、适者生存的进化规律演变而来的随机化搜索法，自从美国的John Holland教授在1975年首次提出以后，它就逐渐发展成为一种通过模拟自然进化过程解决最优化问题的算法模型，在处理最优化问题时表现出非凡优越性。遗传算法求解最优化问题的基本步骤为：

1) 编码：GA在进行搜索之前先将可行域中的解以字符串的方式进行编码（一般采用二进制或浮点数编码），每个编码表示所求问题的一个解，称之为染色体或个体，个体中的每一位字符称为基因；

2) 种群初始化：在可行域中随机产生N个个体，构成一个种群。GA将以这个种群中的所有个体作为进化起点，开始迭代；

3) 适应度评估：根据具体问题设计与之对应的目标函数，即个体的适应度函数，计算每个个体的适应性函数值；

4) 选择：从当前群体中选出适应度较高的个体作为繁殖过程前的样本，即父代个体，选择的原则是：适应性越高，被选择的概率越大；

5) 交叉：以交叉概率选中用于交叉操作的父辈个体，可实行单点交叉或多点交叉。随机选择两个个体的相同位置，在选中的位置实行基因互换。这个过程反映了随机信息交换，目的在于产生新的基因组合，也即产生新的个体；

6) 变异：以变异概率挑选出用于变异操作的父辈个体，在它的编码中随机挑选某一位基因进行反转，得到新个体。同生物界一样，变异发生的概率很低，变异为新个体的产生提供了机会。

通过选择和繁殖产生下一代编码组，重复上述选择和繁殖过程，直到满足条件为止。进化过程最后一代中的最优解就是用遗传算法解最优化问题所得到的最终结果。根据以上步骤，可以得到遗传算法的流程图（见图1）。作为一种快捷、高效的并行算法，遗传算法在求解优化问题中显示出明显的优势。与传统的搜索方法相比，遗传算法具有如下特点：

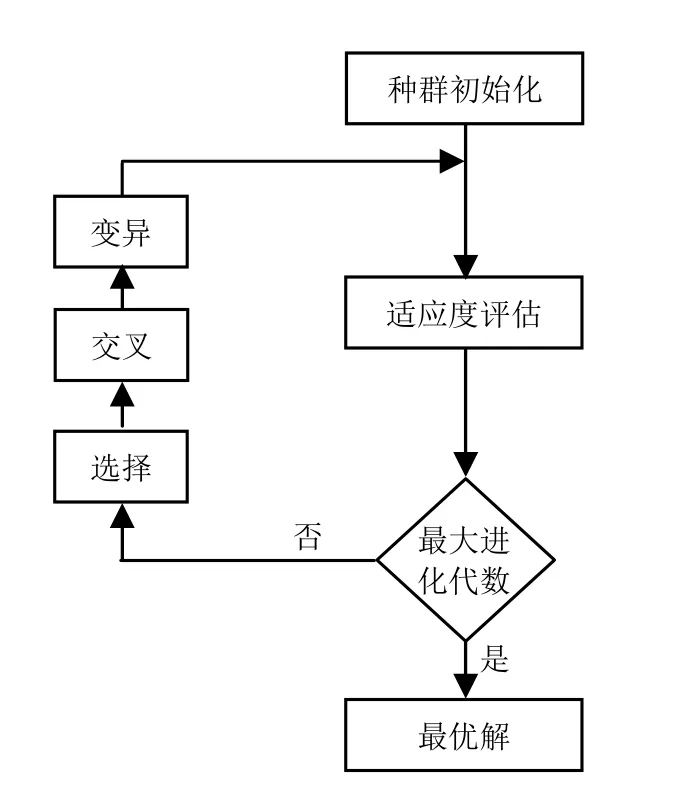
图1 遗传算法流程

1) 搜索过程是从一组解迭代到另一组解，采用同时处理群体中的多个个体，降低了陷入局部最优解的可能性；

2) 使用目标函数值（适应度）进行搜索，无需其他信息；

3) 使用选择、交叉、变异这3个算子都是随机操作，引导搜索趋于最优化。

2 螺旋桨优化设计

2.1 敞水性能计算

假定目标船已完成阻力试验和自航试验，且已初步选定主机。从而有效功率、自航因子及主机信息均已知，螺旋桨推力和扭矩为：

式（1）和式（2）中：T——推力；Q——扭矩；ρ——水密度；n——转速；D——直径；KT和KQ——推力系数和扭矩系数，对于B系列螺旋桨可用多项式表示[6]：

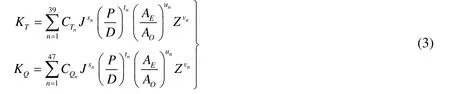
式（3）中：P/D——螺距比；AE/Ao——盘面比；Z——叶数；CTn、CQn、sn、tn、un、vn——均为常数（见表1），J——进速系数：

表1 KT、KQ多项式回归系数及指数[6]

式（4）和式（5）中：VA和VS——进速和航速；w——伴流分数。式（3）适用的雷诺数为Rn=2× 106，对于Rn＞2× 106，计算结果应进行修正，修正方法为[6]：

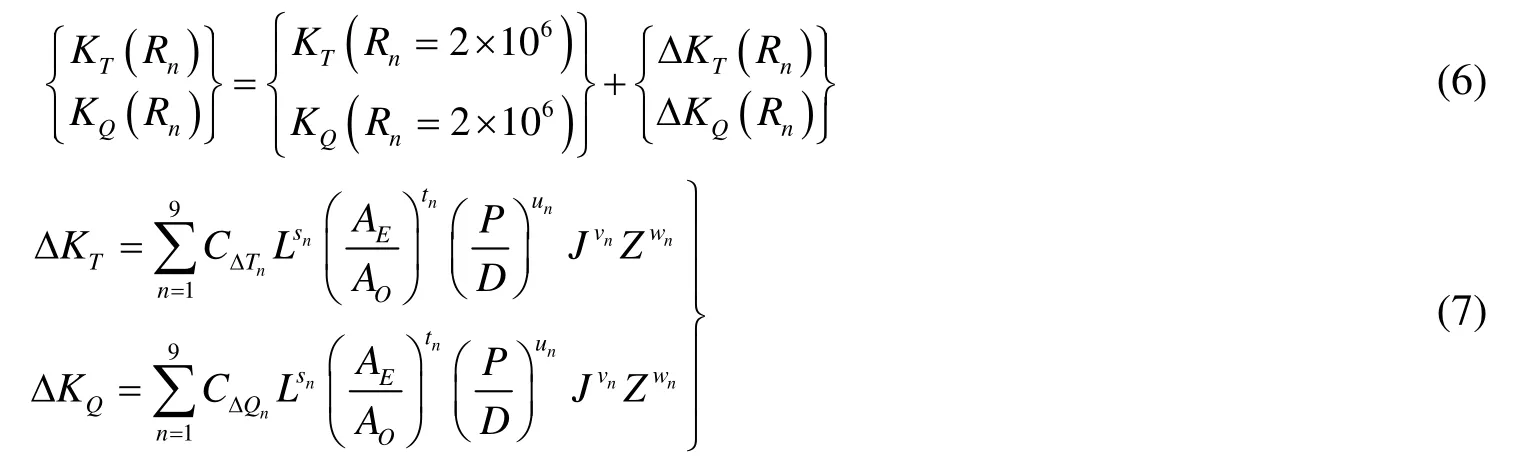
式（7）中：L=log(Rn)-0.301，CΔTn、CΔQn、sn、tn、un、vn、wn——均为常数（见表2）。雷诺数表达为：

式（8）中：υ——运动黏性系数。

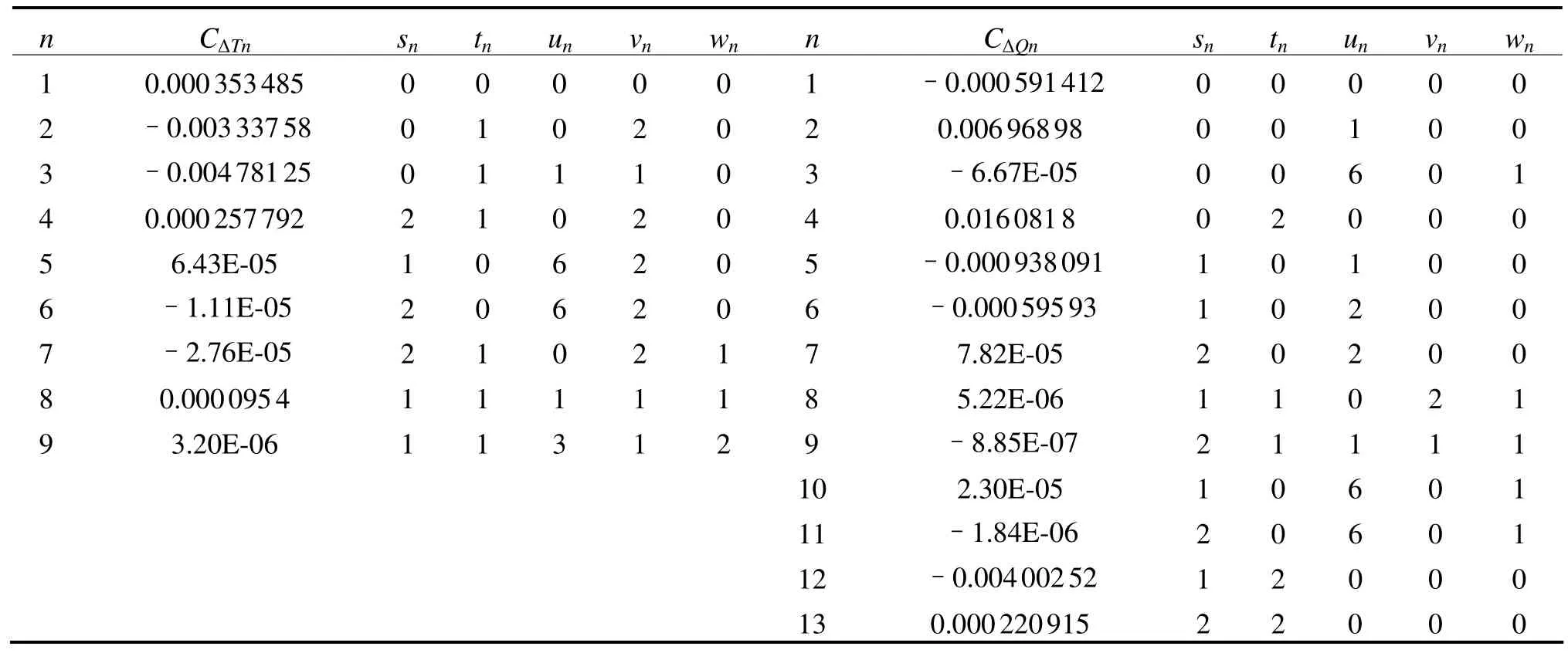
表2 ΔKT、ΔKQ多项式回归系数及指数[6]

2.2 空泡校核

设计桨应具有足够的盘面积以保证不发生空泡，采用Burrill法进行空泡校核，空泡数计算为：

式（9）中：σ0.7R——0.7R半径处空泡数；p0——大气压力；pv——汽化压力；g——重力加速度；h——桨轴浸没深度；V0.7R——0.7R半径处合速度：

由空泡数，从Burrill图中读出单位投影面积的平均载荷系数τc，可计算投影面积AP：

由投影面积Ap计算伸张面积AE：

需求的最小盘面比为：

2.3 航速预报

螺旋桨推力的另一种无因次化形式可由推力载荷系数CT表示[7]：

螺旋桨推力可由阻力和推力减额计算：

式（15）中：R——阻力；t——推力减额，推力系数与推力载荷系数之间的关系为：

式（17）中：PE——有效功率；ηD——推进效率，由船身效率ηH、相对旋转效率ηR和敞水效率η0组成：

由此可根据主机功率预报最终航速。

2.4 优化设计

根据以上分析，螺旋桨优化问题描述为：

目标函数：

约束条件：

式（23）中：PS——主机功率；ηS——轴系传递效率。

3 算例分析

3.1 算例1

以某双机双桨船为例，用上述方法对其进行优化设计。采用5叶B型桨，分别用手工图谱法和GA优化法进行设计。主机及轴系参数见表3，有效功率和自航因子见表4、5，遗传算法参数设置见表6。

表3 主机及轴系参数

表4 满载吃水有效功率

表5 自航因子

表6 遗传算法参数设置

由于遗传算法的随机特点，每次运行结果均不相同。重复运行100次，共耗时约40min，优化结果按航速从小到大排列，得到最优航速12.77kn，具体设计方案见表7。表中同时还给出了手工图谱法设计方案，该方案共历时数小时，得到最佳航速 12.71kn。通过比较可知，与传统手工查图谱法相比，遗传算法具有相当优势。

表7 设计方案对比

3.2 算例2

本算例为集装箱船，采用5叶B型桨，主机及轴系参数见表8，有效功率和自航因子见表9、10，GA参数设置同表6。设计方案见表11。原设计方案航速为22.79kn，本算例耗时约46min，寻找到最优航速23.12kn，遗传算法再次显示出优越性。

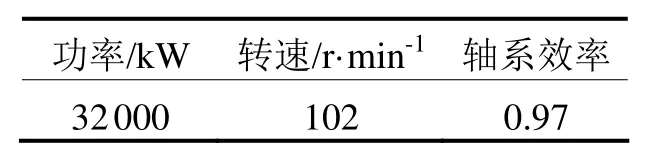
表8 主机及轴系参数

图9 满载吃水有效功率

表10 自航因子

表11 设计方案对比

4 结 语

利用遗传算法对图谱螺旋桨进行优化设计。结果表明，遗传算法的全局搜索能力、并行处理能力、不依赖目标函数导数信息等特点，使其适合求解螺旋桨优化设计问题。

[1] Bertram V. Practical Ship Hydrodynamics[M]. Butterworth-Heinemann. 2000.

[2] Breslin J.P., Andersen P. Hydrodynamics of Ship Propellers[M]. Cambridge University Press. 1994.

[3] Oosterveld M.W.C., Oossanen P.V. Further Computer-Analyzed Data of the Wageningen B-series[J]. International Shipbuilding Progress. Vol.22, No.251. 1975.

[4] Gaafary M.M. Computerized Method for Propeller Design of Optimum Diameter and RPM[A]. 13th Congress of International Maritime Association of Mediterranean, IMAM [C]. 2009.

[5] Ekinci Serkan. A Practical Approach for Design of Marine Propellers with Systematic Propeller Series[J]. Shipbuilding.2011(2).

[6] J.-H. Chen, Y.-S. Shih. Basic Design of a Series Propeller with Vibration Consideration by Genetic Algorithm[J]. Journal of Marine Science Technology. 2007(12).

[7] Carlton J.S. Marine Propellers and Propulsion[M], Second Edition. Butterworth-Heinemann. 2007.