节点修正FDTD法计算薄层色散介质涂覆目标的雷达散射截面*
2013-12-30马亚平秦卫平
马亚平,秦卫平
(南京邮电大学,电子科学与工程学院,南京210003)
近些年来 FDTD[1]处理色散介质[2]薄层方法的研究受到人们的重视,在飞行器的强散射中心涂敷吸波材料或将其设计成隐身结构是降低飞行器雷达散射截面,提高其隐身性能的有效手段。许多微波器件中也都包含有电尺寸小的色散介质薄层,因而包含色散介质薄层电磁问题的数值模拟引起了研究人员的广泛关注。
1987年Yee提出了亚网格技术,提高了计算速度,但亚网格区必须包含整个散射体,因此有一定的局限性[3];2003年文献[4]提出了自由空间中一维色散介质薄层的节点修正法,但只适用于电色散;2005年文献[5]提出利用阻抗边界条件法处理了薄层色散介质问题。2007年文献[6]利用阻抗边界条件及格林函数方法处理了真空中薄层色散介质的反射和透射问题。2008年文献[7]利用等效介质参数法处理了有金属衬底的薄层色散介质的频域特性,随后,文献[8]提出了磁性铁氧体电磁散射的移位算子FDTD方法。2010年,文献[9]提出了一维情况下色散介质混合模型的通用方法。本文将这种算法推广应用到二维FDTD中,以二维TM波为例,采用PML吸收边界[10-11],计算实现涂有色散介质薄层的金属方柱的远场RCS[12]。并将这种结果与细网格比较,证明这种算法在二维算例中同样具有较好的精度。
1 节点的修正
色散介质薄层的介电系数ε和导磁系数μ随频率变化。以洛伦兹模型为例,其介电常数和导磁系数可写为

式中:P为极点数目,ε∞、μ∞为无穷大频率时的相对介电系数和导磁系数,δe、δm为电阻尼系数和磁阻尼系数,ω0e、ω0m为电极点频率和磁极点频率。
入射波为TM波,含有Ez、Hx、Hy3个电磁场分量,如图1所示。图中金属方柱只画出右侧电磁场分量分布。

图1 节点示意图
1.1 电场Ez分量的修正
假定电场在0<x<2Δx区域内是线性分布的,为了满足x=0时切向电场为零的边界条件,设EZ(x)=
为了获得等效介电系数,用介电系数ε来表示色散介质与导体层相邻元胞处的平均电位移矢量DZ。
当介质薄层厚度小于等于元胞尺度的一半时:
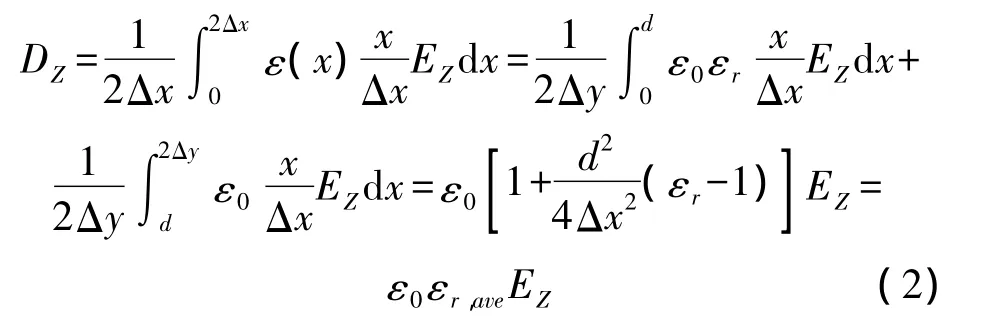
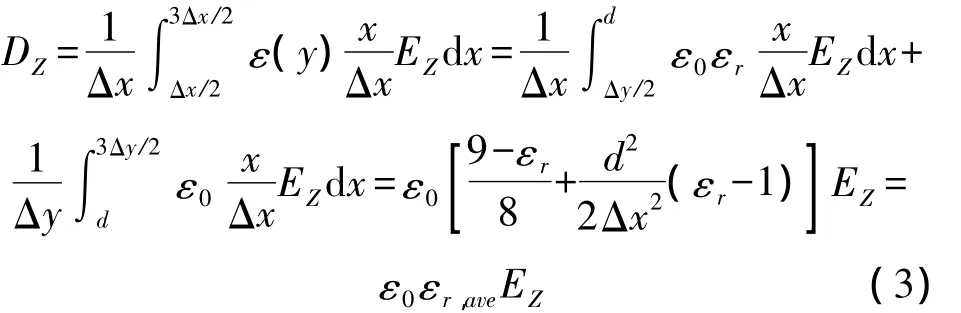
其中:
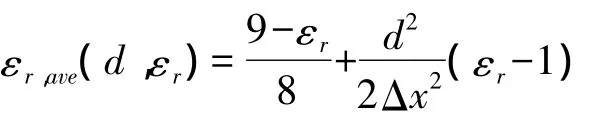
d为介质薄层的厚度,εr为色散介质的相对介电常数,εr,ave为等效相对介电常数。
1.2 磁场节点Hx、Hy分量的修正
对于磁色散,无论色散介质薄层处于真空中还是涂在金属表面,当薄层厚度不足一个元胞时,磁场采样点的磁感应强度均可以由元胞内介质所占比例的加权平均表示:
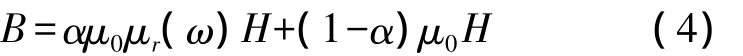
其中(0≤α≤1),整理后可得

其中 μ'(ω)= μr,ave=α(μr-1)+1。
2 算例
应用节点修正时域有限差分法计算无限长金属方柱四周涂有洛伦兹介质薄层时的雷达散射截面RCS(Radar Cross Section)。
金属方柱横截面边长a=0.6 cm,色散介质薄层厚度为d,FDTD元胞尺寸为dx=dy=0.01 m,入射波为时弦波EZ=sin(ωt),时间步长dt=dx/(2c),洛伦兹介质模型中极点P取1,则βm=4×1020rad/s2,ωm=2×1010rad/s,δm=5×109rad/s,γm=1,μ∞=1,βe=9×1020rad/s2,ωe=3×1010rad/s,δe=5×108rad/s,γe=1,ε∞=2。
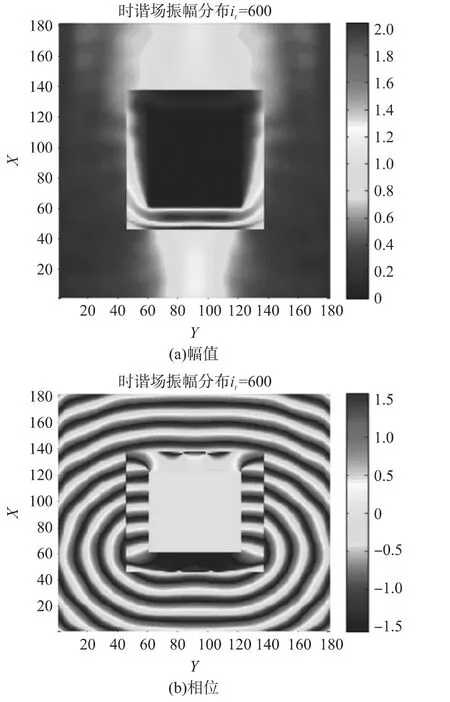
图2 金属方柱基底的薄层洛伦兹介质时谐场振幅和相位分布图
图2为计算所得金属方柱涂覆薄层洛伦兹介质时谐场振幅和相位分布图,图3为不同厚度色散介质薄层的RCS与相应细网格对比图,图4为不同厚度色散介质薄层的RCS比较。
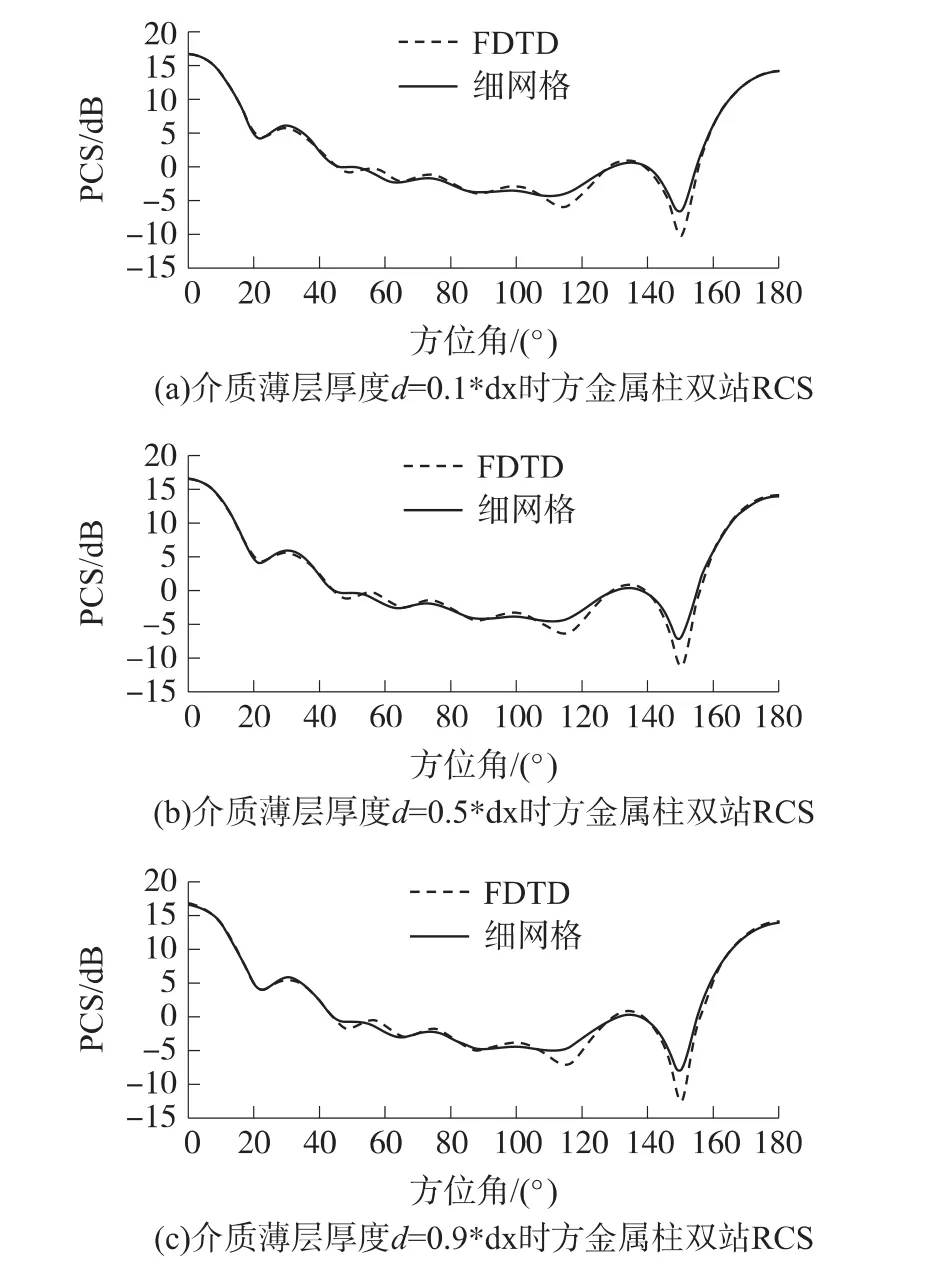
图3 不同厚度薄层的RCS与相应细网格对比图
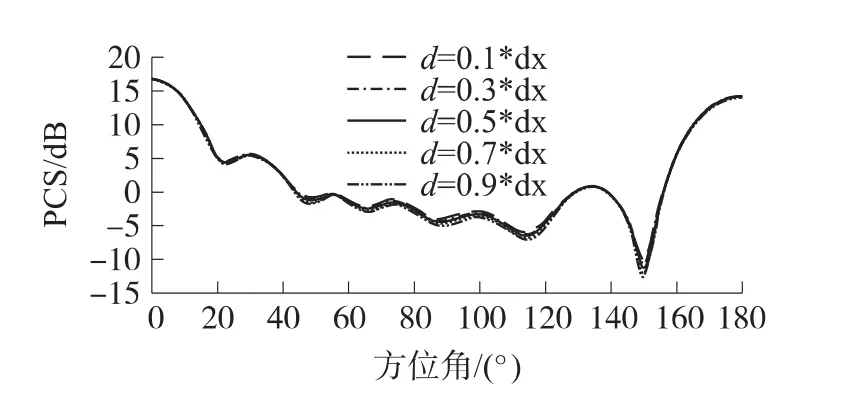
图4 不同厚度色散介质薄层的RCS比较
3 结果
(1)由图2可以直观的看出,金属内部电场为零,在0°方向和180°方向前向散射和后向散射最大;
(2)由图3可以看出,虽然平均系数法和细网格之间存在一定的误差,但误差在可接受范围之内,因为验证了平均系数法的可行性和正确性;

秦卫平(1957-),男,工学博士,教授,主要研究射频/微波、毫米波和太赫兹集成电路和功能器件的设计技术及应用,qinwp@njupt.edu.cn。
(3)由图4可以看出,随着色散介质厚度的增加,RCS呈减小的趋势,反映了介质吸波特性对RCS的减缩效果。
4 结论
本文应用时域有限差分法节点修正技术计算了导体涂覆薄层色散介质的RCS,给出了在二维FDTD中的应用分析,通过与细网格的结果比较分析,此种方法在二维FDTD中同样能够获得良好的精度。
[1]葛德彪,闫玉波.电磁波时域有限差分方法[M].西安:西安电子科技大学出版社,2005.
[2]刘少斌,刘崧,洪伟.色散介质时域有限差分方法[M].北京,科学出版社,2010.
[3]Kasher J C,Yee K S.A Numerical Exanple of a Two Dimensional Scattering Problem Using a Subfrid[J].Applied Computational E-lectromagnetic Society Journal and Newsletter,1987,2(2):75-102.
[4]Mikko K Kärkkäinen.Subcell FDTD Modeling of Electrically Thin Dispersive Layers[J].IEEE Transactions Microwave Theory and Techniques,2003,51(6):1774-1780.
[5]Mikko K Kärkkäinen.Finite-Difference Time-Domain Modeling of Frequency Selective Surfaces Using Impedance Sheet Conditions[J].IEEE Transactions on Antennas and Propagat,2005,53(9):1174-1180.
[6]Giulio Antonini,Antonio Orlandi.Time Domain Modeling of Lossy and Dispersive Thin Layers[J].IEEE Microwave and Wireless Components Letters,2007,17(9):631-633.
[7]董宇航,魏兵,李存志.FDTD模拟金属基底色散介质薄层的节点修正法[J].应用光学,2008.
[8]王飞,葛德彪,魏兵.磁化铁氧体电磁散射的移位算子FDTD分析[J].物理学报,2009,58(7)6356-6362.
[9]魏兵,周允,刘艳峰.色散介质混合模型的通用 FDTD方法[J].微波学报,2010.
[10]Jean Pierre.Perfectly Matched Layer(PM L)for Computational E-lectromagnetics[J].Morgan Claypool,2007.
[11]Cummer S A.A Simple,Nearly Perfectly Matched Layer for General Electromagnetic Media[J].IEEE Micro Wire LETT,2003,13(3):128-130.
[12]Lubbers T J,Tyan D J.A Two-Dimensional Time-Domain Near-Zone to Far-Zone Transformation[J].IEEE Trans Antennas Propagat,1992,AP-40(7):848-851.
