标号树编解码的线性算法

摘要：标号树的编码是一串能够映射一棵标号树结构的标号序列，由于在现代优化算法中便于运算而常常被采用。本文对四种常见的标号树的编解码方法进行了综述，并就标号树直观的边集表示和编码表示之间的转换算法进行讨论，实现了四种标号树编解码的线性算法。

关键词：标号树；Prufer编码；Nevile编码；DM编码

● 引言

标号树是计算机领域中常见的一种数据组织形式，它的传统存储方法通常有双亲表示法、孩子表示法、孩子兄弟表示法、边集表示法等，这些表示方法，在遗传、粒子群等现代优化算法中，由于很难进行运算，所以很少被使用。而标号树的编码是一串可以映射一棵标号树的标号序列，由于其存储简单、便于运算，常常被采用，因而对于标号树编码的深入讨论，无论在计算机的理论还是应用上，都有着十分重要的意义。

1918年Prufer在证明Cayley定理时，最先提出了Prufer编码，1953年Neville提出了三种编码方法，其中第一种和Prufer码一样，后两种称之为Neville2码、Neville3码，近年来Deo和Micikevicius又提出了一种新的编码方法。我们将上述四种编码简称为PR、N2、N3、DM码。

根据编码定义，以上四种编码除DM编解码的算法时间为О（n），其他三种都为О（n2）。近年来一些文献用算法语言给出了它们的线性算法思想。本文在综述上述四种编解码规则之后，用C语言，就标号树直观的边集表示和编码表示之间的转换，给出了编码和解码的线性算法。

● 标号树的编码

1.编码方法

总的来说，四种编码方法都是以叶节点的删除为基础，直至只剩下一条边为止，按照n-2个叶节点的删除顺序，依次将其在删除前的邻接点编号组成一个数字序列，就是其标号树的编码。四种编码的不同在于叶节点的删除顺序不同。

（1）PR编码

删除标号树中最小编号的叶节点；重复第一步，直至该标号树剩一条边。

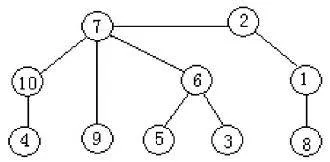
如图1所示的标号树，PR编码的叶子节点删除顺序应为3、4、5、6、8、1、2、9，其相应的邻接点顺序为（6，10，6，7，1，2，7，7）。

（2）N2编码

按升序将标号树的叶节点整批删除；在修正过的标号树上重复第一步，直至该标号树剩一条边。

如图1，N2编码的叶子节点删除顺序应为第一层的3、4、5、8、9和第二层的1、6、10，其相应的邻接点顺序为（6，10，6，1，7，2，7，7）。

（3）N3编码

从最小叶节点开始，逐个删除其所在链上的节点，直至该链被删除；重复第一步，直至该标号树剩一条边。

如图1，N3编码的叶节点删除顺序应为第一条链3，第二条链4、10，第三条链5、6，第四条链8、1、2，其相应的邻接点顺序为（6，10，7，6，7，1，2，7）。

（4）DM编码

按升序将标号树的叶节点整批删除；对修正过的标号树按照其叶节点出现的先后顺序进行整批删除；重复第二步，直至该标号树剩一条边。

如图1，DM编码的叶子节点删除顺序应为第一层的3、4、5、8、9和第二层的10，6，1，其相应的邻接点顺序为（6，10，6，1，7，7，7，2）。

2.编码算法

（1）存储结构

typedef struct node

{ int data；

struct node *next；

} Node；

typedef Node LTree[N+1]；

LTree t；

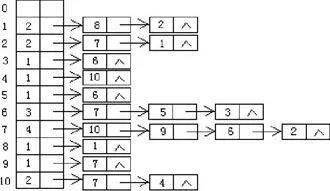
标号树的存储结构采用了图的邻接表存储形式，其说明语句如上，标号树的邻接表存储示意图见图2。将标号树中每个节点i的度数存放在t[i]的data域中，将与该节点i相邻的所有邻接点，以链表链接在t[i]的next域中，为了节点i和t数组下标的一致，这里数组的长度定义为N+1。

（2）PR编码算法

PR编码算法的思想：在邻接表t中顺序查找出第一个度数为1的节点j（t[j].data=1），当前最小的叶节点u=j，求出和u相邻的节点v，写入编码数组，删除最小叶节点u（t[u].data--，t[v].data--）；比较v和j，如果v

PR编码算法实现见函数PR（ ），c数组存放标号树的PR编码；函数GetAdjvex（ ）实现标号树t中求解u节点的邻接点运算。

PR（ LTree t，int c[] ）

{ int i，j，u，v；

u=v=j=0；

for（i=1；i

* { if（v

//找编号最小的叶子节点u

else

{ while（t[++j].data！=1） ；

u=j；

}

v=GetAdjvex（t，u）； // 找叶子u相邻节点v

c[i]=v； //将节点v写入c数组

t[u].data--； t[v].data--； // 删除边（u，v）

}

}

int GetAdjvex（LTree t ，int u ）

{ Node *p=t[u].next；

while（ t[p->data].data==0） p=p->next；

//相邻点度数为0，表该节点已删除

return p->data；

}

函数形式上虽然是二层循环，但while循环所遍历的t数组没有回溯，在整个编码过程中只遍历了一遍；另外求邻接节点GetAdjvex函数中虽然也有循环，但整个编码过程中邻接节点的探查，最多为2N个，所以该编码算法时间效率是线性的。

（3）N3编码算法

N3编码算法的实现参见函数PR（），只要在第五行打“*”的条件语句中去掉v

（4）DM编码算法

DM编码是按层处理叶节点的，所以这里借用一个队列q数组进行分层处理。

将标号树的所有叶节点升序加入队列q中，之后对q进行出队运算，求队头节点u的相邻节点v，删除节点u后的v节点如变成叶子，则加入q队列中。重复出队运算直至队列q为空。

（5）N2编码算法

N2编码和DM编码相似，也是按层处理叶节点的，但每层叶子都要升序排列。这里设计了5个辅助数组（见图3），其中队列q数组的作用仍是分层处理，ql数组存放q数组中对应节点的层数（开始为1层，以后逐层加1），数组tf[u]存放u节点的相邻节点，数组tl[u]存放u节点的层次，数组n[i]存放第i层节点的统计个数。

在分层处理结束后，遍历数组tf中的数据一次，将每个非0数据tf[i]，根据其在数组中的先后位置、数组tl[i]中的层次及数组n[tl[i]]中该层的统计个数，可以计算出该数据在最后编码的位置，其编码算法效率也是线性的。

● 解码

1.解码方法

根据编码序列，还原标号树的边集数据称之为解码。由于编码序列中的数据是和删除叶节点对应的邻接点，所以只要找出叶节点的删除顺序，就可以还原出每条删除的边，也就可以还原出原来的标号树结构。

将编码中的节点按编码顺序依次存放在集合P中，将不在集合P中的节点按升序整理到集合NP中，则NP中的节点即为开始时的叶节点。

（1）PR解码

分别取集合P和NP中最左边的数据u、v连接成边加入到树中；删除u、v，如P中不再出现u则把u按升序加入到NP中；重复第二步骤，直到P为空；将NP中剩下两节点编号连接成边，加入到树中。

（2）N2解码

将NP中所有节点依次和P中左边数据连接成边加入到树中，然后分别从P和NP中删除所有使用过的节点，将P中删除掉的而在后边不再出现的节点按升序加入NP中；重复第二步骤，直到P为空；将NP中剩下两节点编号连接成边，加入到树中。

（3）N3解码

分别取集合P和NP中最左边的数据u、v连接成边加入到树中；删除u、v，如P中不再出现u则把u插入到NP中最前头；重复第二步骤，直到P为空；将NP中剩下两节点编号连接成边，加入到树中。

（4）DM解码

将NP中所有节点依次和P中左边数据连接成边加入到树中，然后分别从P和NP中删除所有使用过的节点，将P中删除掉而在后边不再出现的节点按顺序加入NP中；重复第二步骤，直到P为空；将NP中剩下两节点编号连接成边加入到树中。

2.解码算法

（1）存储结构

以PR编码（6，10，6，7，1，2，7，7）的解码为例，将编码数据存放在c数组中，统计编码中各节点i出现的次数，将其写入数组d中（如图4），则数组d中数据为0的下标，即为不在编码中的节点；每找到一条边，将两端节点在数组d中对应的数据减1，当数据为-1时，表示该节点在NP集合中已删除，当数据减为0时，表示该节点由P集合进入NP集合中。

（2）PR解码算法

PR解码算法的思想和编码相同：在数组d中顺序查找出第一个数据为0的下标j，则当前最小的叶节点u=j，其相邻节点v从c数组中顺序读取，将边（u，v）写入边集数组e中，删除u节点（d[u]--，d[v]--）；比较v和j，如果v

PR解码算法实现见函数PRDecode（ ），在第二个for循环中，内部的while循环由于没有回溯，所以时间效率为线性。

void PRDecode（int c[]，int e[][2]）

{

int d[N+1]={0}， u=0，v=0，i，j；

for（i=1；i<=N-1；i++）

d[c[i]]++； //统计编码中各节点的个数

for（i=1，j=0；i<=N-2；i++）

* { if（v

else

{ while（d[++j]） ； u=j；}

v=c[i]；

e[i][0]=u； e[i][1]=v；//将边（u，v）存入e数组

d[u]--； d[v]--； // 删除u，v节点

}

j=0； // 找NP集合中最后2节点

while（d[++j]）； u=j；

while（d[++j]）； v=j；

e[i][0]=u； e[i][1]=v；

}

（3）N3解码算法

N3解码算法的实现参见函数PRDecode（ ），只要在第七行打“*”的条件语句中去掉v

（4）DM解码算法

DM解码思想和编码一样是按层处理叶子节点的，所以在算法实现中引入一个队列q进行分层处理。DM解码算法效率是线性的。

（5）N2解码算法

N2解码算法思想和DM解码算法相似，也是按层处理叶子节点的，但每层叶子需要重新升序排序。

和N2编码算法设计一样，N2解码设计了4个辅助数组，队列q数组、ql数组、tl数组、n数组，它们的作用和N2编码算法中的辅助数组一样。由于编码顺序即为删除叶节点的邻接节点顺序，所以这里无需数组tf。N2解码算法的也是线性的。

● 结束语

本文给出了标号树常用的四种编码的线性算法，其中DM编解码的线性算法可以根据定义直接求得，而其他三种编码的线性算法借鉴了基数排序的思想，带有一定的技巧性。

参考文献：

[1]王晓东，吴英杰.Prufer编解码的最优算法[J].小型微型计算机系统，2008，04：687-690.

[2]林志庆，吴英杰，王晓东.Neville编解码问题的线性时间算法[J].小型微型计算机系统，2010，10：1984-1988.

[3]Saverio Caminiti，Irene Finocchi，Rossella Petreschi et al. On coding labeled trees[J].Theoretical Computer Science，2007，382（2）：97-108.

[4]Paulius Micikevicius，Saverio Caminiti，Narsingh Deo et al. Linear-time Algorithms for Encoding Trees as Sequences of Node Labels[C]. Congressus Numerantium vol.183.2006：65-75.