《点阵中的规律》教学设计

一、课前谈话：图中的柱子是方的还是圆的？

出示错觉图片，引导学生从不同角度观察。

二、激情导入，点明课题

出示阅兵视频，由具体兵阵图抽象出点阵图。

【意图：用雄壮的阅兵式导入新课，抓住学生的注意力，然后把兵阵抽象成点阵，自然地引出了新课，让学生感受到点阵来源于生活。】

三、多方探究，发现规律

1.一探究

出示第一幅点阵图。

（1）观察思考：①试着用算式表示出点阵中点的个数。

②第5个点阵有多少个点？画出此图形。

（2）生尝试列式画图解答。

（3）交流总结：你发现这组点阵有什么规律？（留出时间让学生充分表达发现的规律）

（4）师小结：横着竖着观察发现第几个点阵就用几乘几，也就是几的平方。

（5）点阵命名。

【意图：根据图形列出算式，使学生的思维顺利地实现了由形——数第一次转换；并且借由画第5个点阵图的过程，感悟数——形的转换，培养学生主动进行数形转换的意识，同时让学生感受“数形结合”的神奇之美。】

2.二探究

（1）提出问题：我们通过横着、竖着观察点阵，发现其中蕴含的规律，还能从别的角度观察并发现其他规律吗？

（2）小组讨论，交流汇报。

汇报一：我是斜着观察（师引导学生先说从什么角度观察， 斜着给点阵划分得到）

第1个： 1；第2个：1+2+1=4；第3个：1+2+3+2+1=9；第4个： 1+2+3+4+3+2+1=16。

师：观察一下，发现什么规律吗？

师：第5个点阵怎样表示？

生：1+2+3+4+5+4+3+2+1（师边板书，写到5问：再往上加吗？）

师： 还有没有从不同角度观察的？

汇报二：我是拐着观察

第1个： 1；第2个： 1+3=4；第3个： 1+3+5=9；第4个： 1+3+5+7=16。

师：你发现什么规律了吗？

生：这次都是奇数相加。

师追问：从奇数几加起？加几个？是随意的几个奇数相加吗？

通过这样的提问，引导学生说出“第几个点阵就从1开始加几个连续奇数”。

师：这位同学的发现有道理吗？（有）验证一下。怎样求第5个点阵的点数呢？（1+3+5+7+9=25）

（5）总结提升：不同角度观察发现不同的规律。

【意图：通过观察、讨论、动手画一画等活动，让学生感受从不同角度观察可以找出不同的规律，在数形转化思想的渗透中，进一步培养学生的观察、分析、总结能力。】

3.再探究

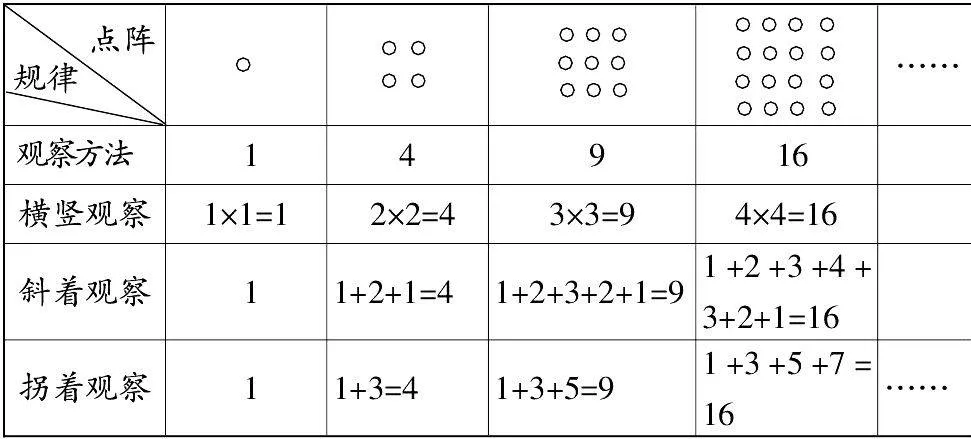
借助列表：（1）展现以上探究全过程和发现的规律，引导学生回忆探究过程，总结研究方法。

（2）找出从不同角度研究的规律的异同点，让学生知道：通过点阵研究数的形式可以多样化。

（3）运用提升：

①如果有81个点，是第（ ）个点阵。

②1+2+3+4+5+6+5+4+3+2+1表示第（ ）个点阵。

③1+3+5+7+9+11+13表示第（ ）个点阵。

【意图：教学不仅停留在让学生发现规律这一结果上，而是让学生对探究的过程进行梳理，引导学生对自己探究性学习方法进行总结；进一步体会数与形，数与式，式与式之间的联系，培养学生利用发现的规律来解决问题的意识和能力。】

四、巩固提升，陶情审美

1.找长方形点阵的规律

师：如果我把正方形点阵改造一下，（点击课件出示第四个点阵）

这是什么形状的点阵？它的前面还有3个点阵。请看

课件出示：你能根据已有点阵，找到它的规律，写出算式并画出第2个点阵吗？

2.拓展运用：创造点阵图。

师：如果老师提供这样一组有规律的数列：4、8、12、16，你能 自创一组有规律的点阵吗？

3.展示交流，结束全课。

【意图：通过先找规律，再写算式，最后补充点阵图，充分的让学生体验形——数——形的转换，并且通过根据规律的数列画点阵图，提供给学生一个开放的空间，让学生的个性得到有效的发展。】

（责编 阮 妮）