模拟混凝土破坏过程的微裂纹模型及其应用
2013-12-29吴佰建李兆霞
吴佰建 李兆霞 郭 力
(东南大学土木工程学院, 南京 210096)
混凝土材料先天性含有大量微观缺陷,在外力的作用下, 微缺陷进行分布式生长聚合形成宏观主裂纹,主观裂纹持续扩展导致混凝土的最终破坏[1].混凝土破坏的细观尺度模拟有两大类方法,第1类方法是Lattice模型[2-5]. 该类方法将物理模型通过某些方式简化成杆件或梁结构模型,并设定杆件破坏规则, 在此基础上进行加载混凝土的破坏过程模拟, 最后将计算结果加以处理,以裂纹等缺陷形式显示.该类方法易于实现, 但与材料实际情况差距较大.第2类方法将连续损伤力学的本构关系引入混凝土的多相材料中[6],将混凝土视作多相连续体进行有限元建模,求解得到混凝土破裂过程.值得注意的是,一些在细观尺度上进行基于多个黏结(cohesive)裂纹[7]或磨平(smeared)裂纹[8-9]的模拟实际上也属于连续损伤力学方法的范畴.这是因为上述方法实际上都是将介质的不连续性(内部缺陷所致)通过某种方式归结到材料的本构关系上,转换成连续介质问题以有利于有限元建模.这类模型的共同点是将宏观现象学方法用于微细观尺度的各个非均质组分.混凝土的各组分都为脆性材料,不具有损伤演化导致的非线性材料特征.此外,混凝土力学行为研究的一个重要问题是定量解释各个组分的脆弹性如何导致了整体的准脆性(即具有一定程度的延性和非线性强化行为),上述基于损伤力学的方法大体上还是用非线性来解释非线性.
与上述两类方法不同,本文的建模直接基于混凝土的失效机理.将初始存在于骨料砂浆界面的裂纹视为主要初始缺陷形式,根据线弹性断裂力学理论模拟裂纹从界面到基体的扩展聚合、主裂纹的形成与扩展、直至混凝土的破坏.本模型是对Krajcinovic模型[10]的推广;实现上述目标的一个主要困难是如何实现裂纹聚合模拟,这也是本文研究的另一个关键问题.
1 混凝土微裂纹模型的建模准则
本文模型的目标是模拟混凝土先天性微裂纹扩展导致材料破坏的过程,建模过程中必须遵循的主要准则有:
1) 先天的初始微裂纹主要存在于砂浆与粗骨料之间的界面上.由于细骨料对裂纹扩展影响不大,这里将细骨料与水泥浆合起来以砂浆的形式加以考虑.此外,将界面过渡区(ITZ)的行为考虑在界面的断裂韧度中,不另加考虑.
2) 裂纹扩展采用线弹性断裂力学的基本准则,即K>KC时裂纹扩展.其中K为裂纹应力强度因子,KC为断裂韧度.这里采用线弹性断裂力学的原因是混凝土的各组分都是线弹性脆性材料.
4) 在失效过程模拟中,采用应力强度因子控制方法,即具有最大K/KC值的裂纹才会扩展.加载过程中不断调整荷载大小以使得最大应力强度因子始终等于断裂韧度.虽然该方法相对应力或者位移控制计算效率较低,但不存在迭代和因此产生的收敛问题,也便于观察混凝土内部状态的逐步变化.
在上述准则导致的微裂纹扩展过程中,会出现裂纹之间的聚合现象,具体包括融合与交叉.其中,裂纹融合的形态如图1(a)所示,裂纹1与裂纹2在某端点相遇,因而实质上融合成一条裂纹.图1(b)显示了2条裂纹的交叉,此时裂纹4扩展并与裂纹3的裂纹面相交,一旦2条裂纹相交,裂纹4的尖端应力奇异性将消失并停止扩展.因此,图1(c)中的情形在理论上不会存在,在本模型中不予考虑.

图1 主要的裂纹扩展形态
2 骨料投放方法
为遵循建模准则1),实现不同级配的骨料在模型中随机投放就成为微裂纹建模的关键,因为实现了骨料的随机投放也就实现了砂浆骨料界面上初始微裂纹的随机分布模拟.
骨料级配被分成几个等级,记为{Gi:i=1,2,…,M}.在等级Gi中,骨料尺寸(即长轴的长度)为在(Di,Di+1)区间上均匀分布的随机变量.在投放之前需要首先估计每个等级的颗粒数.这里骨料被认为是椭圆形的并具有随机的长短轴比r,并假定r在0.5~1之间均匀分布.因此对于等级Gi,单个骨料的面积期望值可计算为
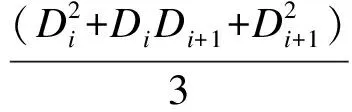
(1)
由此可以得到该等级的骨料代表尺寸为
(2)

(3)
实验室等实验条件是实验教学必备的硬件设施。有些警察高校存在对教学设施管理不规范甚至存在使用混乱、利用率严重下滑、仪器设备落后等问题。
3 混凝土微细观裂纹模型
遵循上述准则,可通过建立混凝土物理模型继而转换得到混凝土微裂纹模型,并遵循相关裂纹扩展准则建立微裂纹扩展和聚合的模拟算法.
3.1 物理模型与裂纹模型
根据上述混凝土破坏机理,初始裂纹都被认为在砂浆/骨料界面产生,并且有可能扩展到砂浆中.界面裂纹与一般裂纹的特征完全不同,数学上裂纹尖端具有的抖动性质[13]使得在有限元模型中容纳该变形和位移模式异常困难.因此一般混凝土的研究中都将界面裂纹处理成普通裂纹[10,14-15].本文将文献[10]中提出的理论模型扩展到混凝土破坏的全过程,从而将混凝土的物理模型简化成裂纹模型.
本模型中,所有的裂纹都被模拟成普通裂纹.不同的是,当裂纹尖端位于砂浆/骨料界面时,断裂韧度取为KC=KC,i; 而当裂纹尖端位于砂浆中时,断裂韧度取值为KC=KC,m.此外,物理模型的裂纹面位于界面的部分都将被映射到颗粒的长轴上.当裂纹模型计算完成后,可以通过逆映射对应到真实的破坏状态.
图2给出了上述简化方法在单个颗粒情形下的示意图,其中粗实线为裂纹面.图3给出了某试样物理模型与理想化模型的实例图.图3(b)中的裂纹是根据各颗粒最大可能的界面裂纹长度而绘制的,不是实际的初始裂纹长度.实际计算过程中,初始裂纹在所示线段上以一定长度比例随机产生.将破坏前的裂纹构形逆影射到物理模型中,形成图3(d)所示的混凝土实际破坏模式.
3.2 微裂纹扩展准则和融合、交叉模拟
初始状态只含有界面裂纹.随着加载的进行,裂纹首先在界面上扩展,之后可能扩展到基体中.本文采用统一的裂纹扩展准则来决定裂纹的扩展.计算等效应力强度因子KJ为

(4)
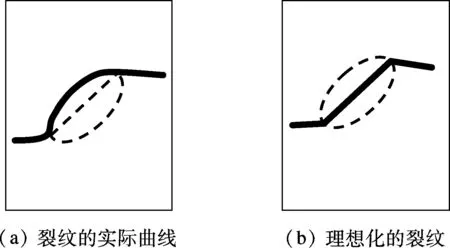
图2 裂纹的实际曲线与理想化的裂纹

图3 混凝土微裂纹模型示意图
式中,KⅠ,J,KⅡ,J分别为裂纹J的Ⅰ型和Ⅱ型应力强度因子.裂纹扩展准则为: 当KJ>KC,J,且KⅠ,J>0时,裂纹扩展,否则不扩展.其中KC,J为裂纹J断裂韧度.根据下面不同情况选取不同KC,J值: ① 裂纹尖端位于界面时,KC,J=KC,i;② 裂纹尖端位于砂浆内时,KC,J=KC,m.
寻找到危险裂纹之后,采用如下准则判断裂纹扩展方向:
1) 若裂纹尖端位于界面上,应用条件①判断是否起裂.若起裂,则立即沿界面扩展至长轴两端.此后,将该裂纹视作一般裂纹,在计算中使用条件②.
2) 如果裂纹尖端处于砂浆内部,应用条件②判断是否起裂,若起裂,利用最大周向应力[16]法则判定扩展方向:

(5)
在进行微裂纹扩展和聚合过程计算时,裂纹面将以向量的方式近似描述,选取裂纹面上合适距离的几何点序列即可较为精确地模拟裂纹的构形,再针对几种主要的扩展和聚合模式,发展了专门的模拟算法,可成功模拟出裂纹的扩展、融合和交叉.这些算法在有限元商用软件ABAQUS的平台上通过面向对象的Python语言接口来实现,这样将有利于混凝土工程结构失效的分析.
4 模型在混凝土拉伸失效过程仿真分析中的应用
本节将上文建立的模型应用于混凝土拉伸失效过程的算例分析.所有的试样都为150mm×200mm的方块,承受拉伸荷载.选取15%,30%,45%,60%4种不同的骨料体积比,分别记为M15,M30,M45,M60.对任一种骨料体积比,随机产生4个试样(如M15,1M15,2,M15,3,M15,,4),并对计算结果进行平均.所有试样都采用相同的骨料级配,如表1所示.出于建模复杂性的考虑,研究过程中将小于8mm的颗粒视作细颗粒,不加以建模.

表1 骨料级配示意图
4.1 失效模式分析
图4给出了部分试样的失效形式.每种混凝土配比选取了2个代表性的试样.可以看出,本模型可以成功地模拟出裂纹融合和交叉,进一步还可以成功地模拟出混凝土破坏全过程(依次包括微裂纹的分布式生长、裂纹聚合、宏观裂纹形成与扩展和试样破裂等).

图4 各级配混凝土试样的拉伸失效图(放大系数10.0)
从这些破坏形式还可以看出,主裂纹形成后大体具有2种失效模式:第1种是该主裂纹一直往前扩展,兼并路径中的各个微裂纹,最终导致失效;第2种是主裂纹会被一些颗粒所阻止而停止扩展,此时其他位置有可能会出现新的主裂纹并继续扩展,甚至可能形成多条主裂纹,因而导致最后的破坏构形含有多个‘眼孔’(eyelets)[17],如图4(c)、 (g)、 (h)所示.总的来说,当骨料体积较小时,第1种模式发生较多; 而当骨料体积增大时,第2种模式发生的可能性增大,当然第1种破坏模式始终占据不小的比例.
4.2 骨料体积比对混凝土拉伸性能的影响
首先将试样的拉伸曲线从计算结果中提取出来,图5为典型的拉伸曲线.从图中可以看出,本模型可以依次计算出混凝土的线性阶段、非线性强化阶段、软化阶段等.对于某些试样,特别是骨料体积较小时,由于混凝土的脆性较强,试样在应力峰值之后会出现所谓跳回(snap-back) 阶段,本模型同样可以模拟出该阶段,此处不再赘述.

图5 某试样的拉伸曲线
如图5所示,从拉伸曲线中可提取出3组控制参数(εth,σth),(εp,σp)和(εu,σu),其中,εth和σth分别表示线性极限应变和应力;εp和σp分别表示强度极限应变和应力;εu和σu分别表示破坏应力和应变.εp/εth和εu/εp反映了材料的延展性,其数值越小,脆性越大,反之则延展性越大.
图6为εp/εth,εu/εp与σp随骨料体积比的变化趋势图,可以看出,随着骨料体积的增加,混凝土的延展性有增大的趋势,而强度呈现减小的趋势.这与文献[1]的实验结果相符,这也从侧面验证了本模型的合理性.

图6 骨料体积比对混凝土性能的影响图
5 结论
1) 本文的数值模型通过对混凝土物理模型一定程度的理想化,在解决了裂纹融合和交叉模拟问题的基础上,成功地模拟出混凝土破坏全过程,包括微裂纹的分布式生长、裂纹聚合、宏观裂纹形成与扩展、试样破裂等.
2) 应用本文建立的混凝土微裂纹数值模型,对混凝土试样拉伸破坏过程进行仿真分析,在大量拉伸试样仿真分析结果的基础上,可定量揭示一些混凝土拉伸破坏的模式与机理.研究结果表明,随着骨料体积的增加,混凝土的延展性有增大的趋势,而强度则呈现减小的趋势.这些结论与已有的实验现象和文献中给出的结果相符,验证了本模型的有效性.
3) 本文提出的模型直接从真实的混凝土破坏机理出发,这与其他基于宏观唯象学的混凝土损伤破坏分析模型有所不同,本文模型可定量描述混凝土材料内部缺陷从微细观到宏观的发展过程,因此可作为混凝土材料和结构失效的数值仿真实验的基础,可为这类材料及其结构的失效控制和安全设计提供参考.
)
[1] Milne I, Ritchie R O, Karihaloo B L.Comprehensivestructuralintegrity2:fundamentaltheoriesandmechanismsoffailure[M]. Oxford:Elsevier Pergamon, 2003.
[2] Bazant Z P, Tabbara M R, Kazemi M T, et al. Random particle model for fracture of aggregate or fiber composites [J].JournalofEngineeringMechanics-Asce, 1990,116(8): 1686-1705.
[3] Schlangen E, Garboczi E J. Fracture simulations of concrete using lattice models: computational aspects [J].EngineeringFractureMechanics, 1997,57(2/3): 319-332.
[4] Lilliu G, van Mier J G M. 3D lattice type fracture model for concrete [J].EngineeringFractureMechanics, 2003,70(7/8): 927-941.
[5] Mungule M, Raghuprasad B K. Meso-scale studies in fracture of concrete: a numerical simulation [J].Computers&Structures, 2011,89(11/12): 912-920.
[6] Wriggers P, Moftah S O. Mesoscale models for concrete: homogenisation and damage behaviour [J].FiniteElementsinAnalysisandDesign, 2006,42(7): 623-636.
[7] Yang Z J, Chen J F. Fully automatic modelling of cohesive discrete crack propagation in concrete beams using local arc-length methods [J].InternationalJournalofSolidsandStructures, 2004,41(3/4): 801-826.
[8] Mohamed A R, Hansen W. Micromechanical modeling of concrete response under static loading-part 1: model development and validation [J].AciMaterialsJournal, 1999,96(2): 196-203.
[9] Deborst R, Vandenboogaard A H. Finite-element modeling of deformation and cracking in early-age concrete [J].JournalofEngineeringMechanics-Asce, 1994,120(12): 2519-2534.
[10] Krajcinovic D, Fanella D. A micromechanical damage model for concrete [J].EngineeringFractureMechanics, 1986,25(5/6): 585-596.
[11] Wang Z M, Kwan A K H, Chan H C. Mesoscopic study of concrete Ⅰ: generation of random aggregate structure and finite element mesh [J].Computers&Structures, 1999,70(5): 533-544.
[12] Stroeven P, Stroeven M. Assessment of packing characteristics by computer simulation [J].CementandConcreteResearch, 1999,29(8): 1201-1206.
[13] Rice J R. Elastic fracture-mechanics concepts for interfacial cracks [J].JournalofAppliedMechanics,TransactionsoftheASME, 1988,55(1): 98-103.
[14] Ortiz M. Microcrack coalescence and macroscopic crack-growth initiation in brittle solids [J].InternationalJournalofSolidsandStructures, 1988,24(3): 231-250.
[15] Huang X, Karihaloo B L. Tension softening of quasi-brittle materials modeled by singly and doubly periodic arrays of coplanar penny-shaped cracks [J].MechanicsofMaterials, 1992,13(3): 257-275.
[16] Erdogan F, Sih G C. On the crack extension in plates under plane loading and transverse shear [J].JournalofBasicEngineering, 1963,85(4): 519-525.
[17] Vanmier J G M. Mode-Ⅰ fracture of concrete-discontinuous crack-growth and crack interface grain bridging [J].CementandConcreteResearch, 1991,21(1): 1-15.
