焊接结构损伤区细观裂纹扩展的分形特征及其多尺度损伤表征

赵超凡 李兆霞

(东南大学土木工程学院,南京210096)(东南大学江苏省工程力学分析重点实验室,南京210096)

焊接区域内部细观裂纹是金属焊接结构中不可避免的主要缺陷,随着结构服役过程中的载荷作用与变形,细观裂纹不断演化,最终发展为宏观裂纹并造成构件及结构破坏,导致灾难性事故的发生.焊接材料宏观看似均匀,但是在细观尺度上却是非均匀的,其损伤演化导致的失效过程涉及到细观尺度的初始缺陷发展到宏观尺度的构件缺陷,属于多尺度损伤演化问题.衡量细观尺度非均匀的分布损伤对宏观刚度和损伤演化的影响,是固体力学的前沿与挑战性课题[1].材料与结构内部在小尺度上的不连续性往往会对其宏观性能产生明显的影响[2],非均匀细观缺陷演化过程对材料与结构宏观性能影响的多尺度描述就成为其关键问题.

近年来,国内外学者对于材料破坏过程的多尺度研究进行了探索和实践,李兆霞等[3-4]针对大型桥梁的损伤劣化过程分析的需要,提出了基于结构的一致多尺度模拟方法,证实了结构损伤与劣化过程分析可以通过结构一致多尺度模拟分析来实现.Shelke 等[5]针对各向异性材料,采用宏观声波信号的方法来研究微观损伤对宏观损伤的影响,并通过信号对比的方法来确定细观损伤程度. Huang 等[6]用弹簧单元将局部细观损伤和无损材料联系起来,通过弹簧弹性系数的改变来反映损伤演化.Vernerey 等[7]将2个尺度上的运动学变量联系起来,提出了一种多尺度连续理论.对于焊接结构,其细观损伤往往是多个裂纹同时共存于一个集中区域,并且裂纹大小、方向及分布都具有随机性和不规则性.这些分布缺陷对材料造成的破坏比单裂纹大得多[8].鉴于初始细观裂纹分布及扩展的复杂性,用以往的细观或者宏观损伤力学理论难以很好地描述材料破坏过程,因此,寻找一种同时适用于宏细观2种尺度的多尺度损伤表征方法就成为一个亟待解决的问题.“分形”作为一个跨尺度适用的概念,可透过复杂且随机的裂纹扩展现象,对不同尺度裂纹扩展进行定量描述,近年来已经被广泛应用于多种材料的破坏过程研究[9-10].

本文综合运用X-CT及电测的试验手段,对焊接构件损伤区进行宏细观损伤演化过程的同步观测,得到了损伤演化过程中细观裂纹扩展特征以及相对应的宏观力学性能劣化过程,研究了细观裂纹扩展过程的分形特征.在此基础上,提出了用于描述焊接结构中的损伤从细观裂纹萌生、扩展、聚合、发展到宏观损伤导致失效的多尺度损伤表征方法,并分别应用宏观损伤实验数据与细观损伤现象对其进行了验证分析.

1 含细观裂纹构件损伤过程实验

1.1 试样设计

为了实现宏细观损伤演化过程的同步观测,选取含对接焊缝的金属板进行拉伸试验,试样母材为Q235A钢,焊材型号为E4303,试样中部通过对接方式焊接.损伤构件的多尺度演化研究,要求试样最小尺度为缺陷尺度的10倍以上.为满足这一要求,确保细观裂纹和构件的尺度关系满足多尺度关系,同时考虑到X-CT对缺陷的分辨率随试样厚度的增加而降低,在试样设计过程中采用X-CT对不同厚度焊接区域进行了多次预扫描,最终确定试样厚度d1=4 mm,此时X-CT能够识别的最小缺陷d2=72 μm,满足多尺度要求.

用线切割的方法对焊缝位置截面进行削弱,使削弱部分在加载状态下产生应力集中,确保焊缝损伤区裂纹在加载过程中扩展明显并由此导致试样最终断裂.焊缝位置的2个应变片布置如图1所示,用于记录损伤演化过程中弹性模量的变化过程,损伤区域的变形取2个应变片的平均值,远离焊缝位置的应变片记录拉伸过程中的名义应力.试验证明焊缝区域断裂时的伸长率小于8%,因此其破坏之前会产生较大的塑性变形,为了保证应变片在这种较大变形情况下不被损坏,试验选取了型号为TA120-55A-C的塑性应变片,该应变片的伸长率为15%,能很好地满足试验要求.试验装置如图1所示.

图1 试验装置

1.2 测试方案与试验过程

载荷方式为应变控制的准静态循环拉伸加载:拉伸至损伤区达到某一应变后卸载，对损伤区进行X-CT扫描并观测其内部微裂纹分布和扩展特征，然后加载到更大的应变后卸载进行X-CT扫描,多次加载至试样完全断裂.损伤区在拉应力作用下,材料内部裂纹在不同方向上均会发生扩展,X光断层扫描可以从3个空间方向获取不同坐标位置的剖面图像,可以判断厚度方向剖面裂纹扩展将最为明显,因而选取厚度方向裂纹分布最多(损伤最为严重)的剖面作为对象,跟踪和观测材料在破坏过程中此剖面的裂纹扩展特征,同时通过应变片记录细观裂纹扩展过程中材料宏观特性的变化情况.X-CT观测剖面示意图如图2所示.

图2 X-CT观测位置及区域的示意图(单位:mm)

2 细观裂纹扩展的分形特征

2.1 细观裂纹扩展图像记录与处理

随着载荷的增加,试样发生了明显的塑性变形,弹性模量不断减小,说明随着塑性变形的增加,材料内部以细观裂纹为主的损伤不断发生演化，导致试样的宏观力学性能劣化.因此,需要通过X-CT对焊接试样损伤区内部裂纹扩展特征进行观测与分析.

裂纹观测记录的扫描原始图片为灰度图,灰度较大的位置即为裂纹位置.为了便于后续计算分析和不同应变时的图像比对分析,需要将灰度图进行处理,采用Matlab工具将灰度图转换为黑白二值图,转换后的结果如图3所示.

图3 图像二值化

图4和图5给出了加载过程中与试样变形同步记录的焊接试样损伤区内部裂纹扩展图像，图5为图4各卸载点所对应的裂纹扩展图像.可以发现,随着塑性变形的增加,损伤区内部不断发生细观裂纹的扩展和聚合,同时也有新的细观裂纹萌生.

由图5可以看出,试样变形过程中的损伤演化表现为其内部裂纹的萌生、扩展及聚合,其中以裂纹扩展和聚合为主,也有部分新的细观裂纹萌生.新裂纹萌生的位置往往是裂纹分布相对较少的位置(如图5(d)、(f)中虚线圆框的位置),随着变形增加,裂纹分布逐渐集中于一条带状区域内(见图4(h)中虚线方框位置).c点之前损伤演化以现有裂纹扩展为主,c点之后随着塑性变形的增加,不断有新的裂纹萌生,以及原有裂纹的扩展与聚合.当应变达到d点时,裂纹分布逐渐呈现出垂直于载荷方向的带状分布,随着塑性变形的增加,损伤演化基本都发生于带状范围内,其他位置基本不再发生损伤演化,实验证明试样最终也断裂于这一带状范围之内.相比中间位置的裂纹,位于试样边缘且垂直于载荷方向的裂纹扩展速度较快,且扩展方向明确,最终造成试件由此断裂,由此可见边缘裂纹对试样破坏的影响更大.

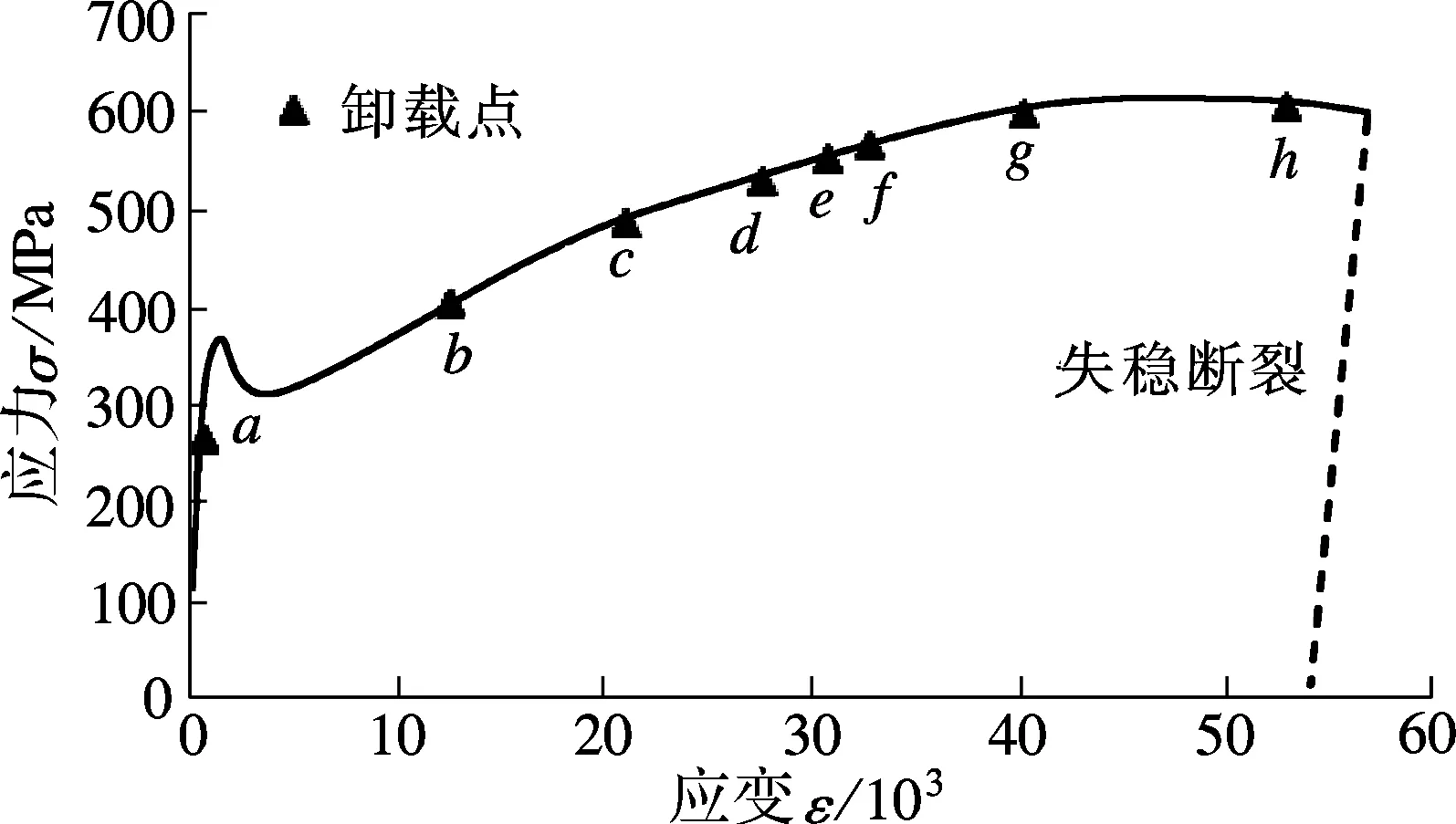
图4 拉伸过程中卸载点

图5 试样变形过程中细观裂纹扩展过程

比较图5给出的在试样变形过程中同步记录的细观裂纹扩展过程,尤其是比较不同变形状态下的(见图5(a)～(h))裂纹扩展过程中表现出来的在裂纹发展形态上的自相似性,可以发现它们表现出显著的分形特征.

2.2 分形维数计算方法

分形是对自然界和非线性系统中出现的不光滑和不规则几何形体的相似性特征的一种定量描述.将以前不能定量描述或难以定量描述的复杂对象用一种较为便捷的定量方法表述出来.分形维数是分形理论中的一个重要概念,是用来定量表示自相似形状和现象的最基本量[11].分形维数有多种定义方法,其中盒维数法应用最为广泛,分形理论中许多维数的概念都是盒维数的变形,并且盒维数法本身易于程序化计算,所以本文中的分形维数采用盒维数.

盒维数法的定义为:用正方形格子(δ×δ)去覆盖分形图形,对于给定的尺码δ,可以算出盒子数目N(δ),随着δ的变化,有一系列对应的N(δ),则盒维数计算式为

(1)

求解盒维数的具体步骤为:

① 用边长为δ的正方形对试验照片或模拟图形进行网络化分割,计算出其中包含有裂纹的格子数目N(δ);

② 改变δ的值,可以得到多组δ和N(δ),对δ和N(δ)进行分析,判断其是否满足N(δ)∝δ-D,如果满足,则说明裂纹分布具有分形特征,d即为其分形维数.

2.3 细观裂纹及其扩展形态的分形度量

按照分形维数的计算方法编制Matlab程序,对裂纹分布的二值化图像进行分形维数计算,用分形维数的网格法计算出所需的数据点,再用最小二乘法拟合分形维数.以图5中a点的细观裂纹图像为例,用编制的程序对其进行分形维数计算,计算结果如图6所示.

用同样的方法对图5中裂纹扩展过程的8幅图像分别进行分形维数计算,获得的分形维数随塑性变形的变化趋势如图7所示.计算结果表明所有

图6 ε=0. 297状态下的裂纹形态分形维数计算

拟合直线的线性相关系数R2均大于0.998,这说明计算得到的分形维数具有足够的可信度,也表明试样变形过程中记录的细观裂纹扩展形态确实具有显著的分形特征,能够用分形维数来度量.

图7 分形维数随塑性变形的变化趋势

由图7可以看出,随着塑性变形的增加,焊缝区裂纹扩展过程的分形维数呈线性增加趋势.这是因为,初始裂纹呈随机分布,随着塑性变形的增加,裂纹演化模式主要表现为扩展和贯通,由于损伤在细观尺度上的不均匀性,裂纹演化的结果将会出现一条或几条裂纹分布相对密集的区域,相对密集的裂纹分布造成其分形维数增加,同时更有利于裂纹密集区域的损伤演化,从而使分形维数进一步增加.可见,虽然裂纹分布及扩展形态表面上具有不规则性,但是可以通过分形维数来定量描述这种裂纹扩展形态的变化规律.

3 焊接结构损伤区裂纹扩展过程的多尺度损伤表征

3.1 细观裂纹扩展的分形损伤度量

对于含有分布细观裂纹损伤的区域,损伤量化很大程度上取决于裂纹的数量及长度,同时裂纹的分布及扩展特征对其材料损伤的影响不容忽视.既然裂纹扩展形态具有很好的分形特征,而分形维数的概念可以很好地将裂纹的“集中程度”量化,因此,对于确定的具有分形特征的细观裂纹损伤区域,可定义如下损伤度量:

(2)

式中,A为损伤区域面积;∑l为区域内所有分布裂纹的总长度,随着载荷的增加,∑l会逐渐增加,表征裂纹“集中程度”的分形维数d也在不断发生变化.此分形度量是在细观裂纹的基础上,综合考虑了所有细观裂纹总长度以及裂纹扩展过程所表现出的整体分形特征,是所有细观裂纹表现出的材料整体特性,物理意义更加明确.

3.2 多尺度损伤表征

将损伤度量进行无量纲规格化，即

(3)

式中,ψ0为初始状态时的损伤度量;ψf为试件断裂时的损伤度量;ψ为损伤演化过程中的损伤度量;ω(D)为规格化后的损伤表征量.

初始状态时，ψ=ψ0,ω(D)=0;材料断裂时，ψf=ψ0,ω(D)=1；材料变形过程中，随着裂纹萌生与扩展，则ψ0<ψ<ψf,0<ω(D)<1.

结合试验数据和裂纹扩展图像,用ω(D)的表征方法对图4的裂纹扩展过程进行损伤演化计算,结果表明损伤量ω(D)随塑性变形ε的增加呈线性增加趋势,计算结果如图8所示.

图8 ω(D)随塑性变形的变化趋势

在细观裂纹—宏观裂纹—材料断裂的过程中,ω(D)的值从0逐渐演化至1.损伤演化初期,ω(D)较小,此时材料损伤主要表现为细观裂纹的随机扩展及萌生;随着材料损伤演化,细观裂纹逐渐扩展和贯通,局部区域开始出现集中细观裂纹,并最终发展为宏观可见裂纹,此时远离宏观裂纹的区域细观裂纹扩展缓慢或停止,损伤演化以宏观裂纹扩展和贯通为主,裂纹扩展形态仍具分形特征,ω(D)此刻同时描述了宏观和细观裂纹扩展过程.综上所述,ω(D)在整个破坏过程中既描述了宏细观裂纹的演化过程,又反应了所有宏细观裂纹所表现出来的整体宏观特性,是一个多尺度损伤表征量.

3.3 多尺度损伤表征方法的验证分析

目前损伤力学理论主要分为宏观损伤力学和细观损伤力学2个分支,其中损伤宏观唯象理论中的连续损伤变量主要是以有效承载面积来定义的,但是从细观上对每一种缺陷形式和损伤机制进行分析以确定有效承载面积是很困难的.因为受损后材料的弹性模量下降,由此可以通过测量卸载弹性模量来计算损伤变量,根据应变等效原理,可得

(4)

(5)

(6)

(7)

对于微裂纹扩展的细观损伤描述,Murakami等[12]发展了一种三维各项异性损伤理论，认为损伤是由微裂纹的发展造成的.这些缺陷的演化导致了有效承载面积减小、材料承载能力下降以及材料力学性能的劣化,这些变化依赖于当前的应力和损伤状态,是各向异性的.材料的损伤状态可以用一个二阶对称张量来表示，即

(8)

以上2种不同尺度下的损伤定量描述所能解决的问题仅限于在其定义尺度下的损伤问题,但金属材料破坏问题是一个细观到宏观的多尺度损伤的演化过程,单纯用某一个尺度的损伤理论无法描述构件破坏的完整过程.

从细观裂纹演化到宏观裂纹直到构件最终断裂,裂纹扩展形态始终存在着明显的分形特征.本文所提出的多尺度损伤表征综合考虑了裂纹扩展过程中,宏细观裂纹长度和裂纹扩展分形维数的变化,研究对象为所有尺度的宏观和细观裂纹.同时用分形反映不同尺度裂纹扩展过程的不均匀性,能够很好地描述细观至宏观的多尺度损伤演化过程.

为了验证本文提出的多尺度损伤表征方法,这里基于图4的裂纹扩展过程中的细观裂纹量化结果以及与之同步发生的试样变形过程中有效模量的变化,分别对式(7)给出的宏观损伤和式(8)描述的细观损伤进行计算,并对计算结果做规格化处理,其中,设初始状态时损伤变量为0,试样断裂时损伤为1.将得到的计算结果与式(3)的多尺度损伤表征结果进行对比,结果如图9所示.结果表明，多尺度损伤表征方法在宏观和细观2个尺度与现有的损伤表征方法吻合较好.

图9 多尺度损伤表征验证

4 结论

1) 综合运用X-CT和电测法对焊接构件的损伤演化过程进行细观和宏观的同步观测,发现随着试样宏观塑性变形的增加,损伤跨尺度演化的结果在宏观尺度上表现为构件有效模量的减小,在细观尺度上表现为内部细观裂纹的扩展和聚合,在原来无裂纹的位置还有少数细观裂纹萌生.

2) 在损伤跨尺度演化过程中观测到裂纹的扩展形态具有显著的分形特征,计算得到的分形维数具有足够的可信度,表明试样变形过程中记录的细观裂纹扩展形态确实是具有显著的分形特征,能够用分形维数去度量.在焊接构件变形与损伤演化过程中,表征损伤区裂纹扩展的分形维数随塑性变形呈线性增加趋势.

3) 提出了一种全新的多尺度损伤表征方法,这种表征方法具有跨尺度的物理意义;分别用现有的宏观损伤和细观损伤表征方法对其验证,结果表明新的多尺度损伤表征方法与现有的单一细观和单一宏观尺度下的损伤表征方法各自吻合较好.这表明,新的多尺度损伤表征方法能够很好地描述焊接结构中的损伤从细观裂纹萌生、扩展、聚合、发展到宏观损伤导致失效的多尺度演化过程.

)

[1] 白以龙,汪海英,柯孚久,等.从“哥伦比亚”号悲剧看多尺度力学问题[J].力学与实践,2005,27(3):1-6.

Bai Yilong, Wang Haiying, Ke Fujiu, et al. A view on multi-scale mechanical problems from COLUMBIA tragedy[J].MechanicsandEngineering, 2005,27(3):1-6. (in Chinese)

[2] Sih G C.Use specification of multiscale materials for life spanned over macro-,micro-,nano-,and pico-scale [J].TheoreticalandAppliedFractureMechanics,2010,53(2):94-112.

[3] 李兆霞,王滢,吴佰建,等.桥梁结构劣化与损伤过程的多尺度分析方法及其应用[J].固体力学学报,2010,31(6):731-756.

Li Zhaoxia, Wang Ying, Wu Baijian, et al. Multi-scale modeling and analyses on structural deterioration and damage in long-span bridges and its application[J].ChinsesJournalofSolidMechanics, 2010,31(6): 731-756. (in Chinese)

[4] 郭力,李兆霞,陈志文. 面向结构状态评估的多尺度损伤模型[J]. 东南大学学报:自然科学版,2010,40(5): 1047-1051.

Guo Li, Li Zhaoxia, Chen Zhiwen. Structural state assessment oriented multi-scale damage model[J].JournalofSoutheastUniversity:NaturalScienceEdition, 2010,40(5): 1047-1051. (in Chinese)

[5] Shelke A,Banerjee S,Kundu T,et al.Multi-scale damage state estimation in composites using nonlocal elastic kernel:an experimental validation[J].InternationalJournalofSolidsandStructures,2011,48(7/8):1219-1228.

[6] Huang Y, Gong X Y, Suo Z,et al.A model of evolving damage bands in materials[J].InternationalJournalofSolidsandStructures,1997,34(30):3941-3951.

[7] Vernerey F, Liu W K,Moran B.Multi-scale micromorphic theory for hierarchical materials[J].JournaloftheMechanicsandPhysicsofSolids,2007,55(12):2603-2651.

[8] Chaussumier M,Shahzad M,Mabru C,et al.A fatigue multi-site cracks model using coalescence, short and long crack growth laws, for anodized aluminum alloys[J].ProcediaEngineering,2010,2(1):995-1004.

[9] Carpinteri A,Puzzi S.The fractal-statistical approach to the size-scale effects on material strength and toughness[J].ProbabilisticEngineeringMechanics,2009,24(1):75-83.

[10] Zho J W,Xu W Y, Yang X G.A microcrack damage model for brittle rocks under uniaxial compression [J].MechanicsResearchCommunications,2010,37(6):399-405.

[11] Tang H P,Wang J Z,Zhu J L,et al.Fractal dimension of pore-structure of porous metal materials made by stainless steel powder [J].PowderTechnology,2012,217:383-387.

[12] Murakami S, Ohno N.Acontinuumtheoryofcreepandcreepdamage[M]//CreepinStructures. Berlin,Germany: Springer Berlin Heidelberg, 1981:422-444.