低频P波荷载下压电介质中共面裂纹的耦合断裂行为
2013-12-29张培伟
张培伟
(东南大学土木工程学院,南京 210096)(东南大学江苏省工程力学分析重点实验室,南京 210096)
压电结构的应用往往与动载荷密切相关,通过交变电流的激励可以引起此类结构的振动,也可以在受到变形后输出电信号.因此,一些制造缺陷或在服役中形成的裂纹,常会导致压电结构精度降低甚至是完全失效.为了保障压电元器件的可靠性,必须对有缺陷的压电材料进行深入研究,才能有效评价此类元件的性能.
目前,已有大量关于含缺陷压电材料的平面问题和反平面问题的研究工作可供参考,但是这些结果对于三维空间问题却并不完全适用.在空间问题的研究中,可以将裂纹看作是一层空气或真空薄层,有时假设空洞层为圆形或椭圆形,有时假设薄片为矩形,当空洞层的面积大小相当时,按照矩形假设所计算得到的结果对于工程应用来说一般是偏安全的.Zhang等[1]利用一般Almansi理论研究过矩形裂纹,给出了矩形裂纹的长宽比对压电材料安全性的影响规律,同时还发现,动荷载与静荷载作用下裂纹的扩展形式并不相同,在静载荷下矩形裂纹长边的中点更容易首先发生扩展,而在动载荷作用下却并非如此.
为了迎合复杂服役环境的需求,压电材料的动态断裂研究尤为重要,因为关于压电材料静态断裂的大量工作对于动态服役的压电元件的安全评估显然是不充分的.Zhao和Meguid[2]研究了含有多个共线界面裂纹的压电层合板的动态断裂,发现越小的裂纹越容易扩展并最终导致结构破坏.Liu和Zhong[3]研究了2个共线裂纹在面内冲击荷载作用下的行为,计算结果显示了电场方向对于裂纹扩展的促进和阻碍规律.
本文采用部分电导通边界条件,研究了压电介质中一对共面矩形裂纹的耦合断裂问题.通过数学建模和变换,将断裂问题转化为求解一组对偶积分方程,并经过严格的数学推导得到广义应力场的解析解,进而得到了广义强度因子和能量释放率的解析表达式.最后,利用一系列的数值算例,详细讨论了裂纹耦合断裂的一些规律.
1 模型建立
根据常见压电结构的工艺和破坏形式,假设压电材料为均质横观各向同性材料,材料的各向同性面平行于x-y平面,2个共面的裂纹位于同一各向同性面内(z=0).采用等面积的矩形拟合裂纹,可以为结构评估提供偏安全的结果,矩形尺寸如图1所示.常用压电器件的载荷通常沿着压电材料的极化方向,即z轴方向,设简谐应力载荷的形式为σzz(x,y,0)=-σ0eiωτ,其中σ0和ω分别为周期载荷的幅值和圆频率,τ为时间变量.载荷的激励源视为无穷远处,因此可以将载荷引起的应力波近似为平面波处理.
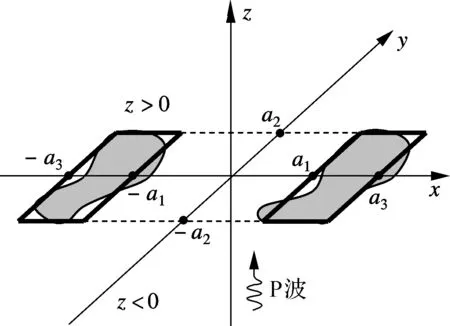
图1 共面矩形裂纹几何尺寸
对于远场为简谐荷载作用的断裂问题,根据线弹性叠加理论,可以求解在裂纹上、下表面施加与远场动载相同频率和振幅的扰动载荷问题.在理想线弹性体中,包括应力、应变和交变电场等物理量都符合如下的变化规律:
(1)
式中,X可以表示弹性体内位移uk、电势φ、应力σkl以及电位移Dk(k=x,y,z;l=x,y,z);上角标j=1,2分别表示弹性体位于z=0平面上、下方的物质空间.不计体力和自由电荷,压电介质的平衡方程和本构方程可以分别表示为
(2)
(3)
(4)
式中,
ρ0,cpq,epq,εpq(p=1,2,3;q=1,2,3)分别表示压电介质的密度、弹性常数、压电系数和介电常数.
将本构方程(3)和(4)代入到平衡方程(2),得到位移和电势表示的压电介质控制方程为
(5)

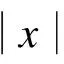
(6)
在裂纹面以外的区域,位移、应力、电位移和电势满足连续性条件为
X(1)(x,y,0+)=X(2)(x,y,0-)
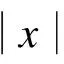
(7)
在距离裂纹区域足够远处有
ux(x,y,z)=uy(x,y,z)=uz(x,y,z)=φ(x,y,z)=0
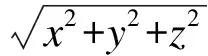
(8)

2 边界值问题的求解
2.1 基本解
压电介质中的位移可以用位移势函数Ψ(j)和G(j)表示,即
(9)
将其代入到控制方程(5)可得
(11)
式中,Δ=∂,xx+∂,yy表示二维拉普拉斯算子.参考文献[6-7],可以求得位移势函数、位移分量、电势、应力分量和电位移分量的表达式为
(12)
(13)
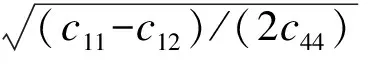
2.2 位移阶跃函数
定义裂纹上、下表面之间的位移阶跃函数为

(15)
(16)
(17)

对方程(15)~(17)进行二维傅里叶变换[9],得
(18)
(19)
(20)
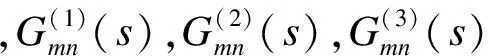
2.3 对偶积分方程的求解
将位移、应力、电势和电位移的表达式(12)~(13)代入到边界条件(6)和(7)以及位移阶跃函数(14)中,经过傅里叶变换后可得
(21)
(22)
a1≤x≤a3, 0≤y≤a2
(23)
(24)
式中,
[mij]4×4=M-1, [nij]4×4=N-1
将式(18)~(20)代入到方程(23)~(24)中,方程(24)始终自动满足.对方程(23)关于x在区间[a1,x]上积分并关于y坐标在区间[0,y]上积分,可得
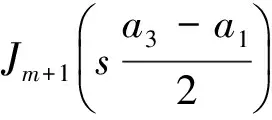
sin(ty)dsdt=-σ0(x-a1)y
a1≤x≤a3, 0≤y≤a2
(25)
[cos(sa1)-cos(sx)]sin(ty)dsdt=0
a1≤x≤a3, 0≤y≤a2
(26)
[sin(sx)-sin(sa1)][1-cos(ty)]dsdt=0
a1≤x≤a3, 0≤y≤a2
(27)

3 断裂准则
3.1 广义强度因子
由断裂力学理论,需求裂纹尖端处广义应力场.可令式(13)中z=0,即得裂纹尖端场.但当积分变量趋于无穷大时,需要通过如下的关系式来消除积分方程在裂纹边缘处(x=a1,x=a3,y=a2)的奇异性[8]:
(28)
(29)
考虑到问题的对称性,下面仅研究x≥0且y≥0区域的情况.经过处理后的裂尖应力和电位移表达式如下:
1) 当0≤x (30) 2) 当a2 (31) 利用裂尖应力和电位移场的表达式(30)~(31),可得裂纹前端广义应力强度因子的表达式如下: 1) 在裂纹的内边缘处,即x→a1且0≤y (32) (33) 2) 在裂纹的外边缘处,即x→a3且0≤y 3) 在裂纹的上边缘处,即y→a2且a1 (36) (37) 利用裂纹闭合能量的概念,以及应力、位移、电位移和电势的渐进闭合概念,I型裂纹扩展的能量释放率G的表达式为 Dz(r,0)φz(Δc-r,π)]dr (38) 式中,Δc为裂纹闭合的长度. 裂纹上下表面的位移和裂纹上下表面的电势分别为 a1 (39) a1 (40) 将裂尖应力表达式(13)、裂纹面位移表达式(39)和裂纹面电势表达式(40)代入到能量释放率表达式(38)中,得 (41) 表1 BaTiO3 的相关参数 图2~图6给出了裂纹各边中点处应力强度因子、电位移强度因子和能量释放率随载荷圆频率变化的情况.对比各图可见,在相同的裂纹几何尺寸、载荷属性等条件下,各断裂准则参数具有相同的变化规律,区别仅是数值大小不同.因此,除了少数几种特殊情况外,采用这2种断裂准则判断的结果具有一致性. 图2 裂纹各边中点处断裂参数随载荷频率变化曲线(a2=1.0,a3=1.1,D0/ε0=1.0×108) 图3 裂纹各边中点处断裂参数随载荷频率变化曲线(a1=0.3,a2=1.0,a3=1.3,D0/ε0=1.0×108) 图4 裂纹各边中点处断裂参数随载荷频率变化曲线(a1=0.5,a2=1.0,a3=1.5,D0/ε0=1.0×108) 图5 裂纹各边中点处断裂参数随载荷频率变化曲线(a1=0.1,a2=1.0,a3=0.2,D0/ε0=1.0×108) 图6 裂纹各边中点处断裂参数随载荷频率变化曲线(a1=0.1,a2=1.0,a3=0.5,D0/ε0=1.0×108) 在低频载荷作用下,曲线的第1个极值出现在ω≈6 000 rad/s的附近.这表示当载荷频率在这附近时,图2和图3中所示尺寸的裂纹最有可能发生扩展.图2和图3的区别在于,针对2种不同的裂纹尺寸,在不同激励载荷频率下,裂纹首先发生起裂的位置有所区别.当2个裂纹之间的距离较近时,裂纹内边较容易首先发生扩展,也就是说,2个矩形裂纹很可能会扩展并联通为1个更大的裂纹;当2个裂纹之间的距离较远时,较高的载荷频率会引起2个裂纹分别沿裂纹外边缘扩展,从而形成2个较大的裂纹.对照图3所示的情况,当ω>6 000 rad/s时裂纹外边首先扩展.由图4可知,增大裂纹区域的面积,裂纹外边的断裂准则参数持续增大,而裂纹内边和上边的断裂准则参数则逐渐减小,这意味着裂纹更容易向外扩展. 当裂纹沿x轴方向变窄时,图5和图6给出了载荷频率对裂纹扩展行为的影响.裂纹上边的断裂准则参数过小,故没有在图中出现.该算例所研究的载荷频率范围内,曲线并没有出现极值.为了进一步研究裂纹宽窄对断裂准则参数的影响,给出了如图7所示的算例.由图可知,随着裂纹宽度的增大,裂纹更容易发生扩展. 图7 裂纹各边中点处应力强度因子随a3的变化曲线(ω=6 000,a1=0.1,a2=1.0,D0/ε0=1.0×108) 图8为裂纹各边缘中点处的应力强度因子变化曲线.由图可知,裂纹外侧边缘的应力强度因子较大,也更容易发生开裂.然而,在进一步更详细的研究中发现,图8所表示的结果并不能准确给出裂纹起裂点.图9给出了图8算例中裂纹边上各点的应力强度因子,可以明显看出,断裂准则参数最大值并非出现在裂纹边缘的中点处,因此不能仅根据裂纹中点处的应力强度因子来判断裂纹的起裂情况.为了准确评估裂纹的扩展行为,将各频率下裂纹边上应力强度因子的最大值提取出来,并绘于图10中.由图10可知,随着裂纹宽度的增加,裂纹上边缘发生扩展的可能性逐渐变大. 图8 裂纹各边中点处应力强度因子随载荷频率变化曲线(a1=0.1,a2=1.0,a3=2.1,D0/ε0=1.0×108) 图9 裂纹各边应力强度因子分布情况 (ω=2 000,a1=0.1,a2=1.0,a3=2.1,D0/ε0=1.0×108) 图10 裂纹各边最大应力强度因子随载荷频率变化曲线(a1=0.1,a2=1.0,a3=2.1,D0/ε0=1.0×108) 通过对压电介质中2个共面裂纹耦合断裂问题的研究,考虑裂纹的部分电导通特性,得到了载荷频率和裂纹宽度对裂纹扩展的影响规律.与静载荷作用下的裂纹扩展估计不同,仅采用裂纹边上中点处的应力强度因子或能量释放率并不能完全准确地预测裂纹行为,必须对裂纹边上各点的应力强度因子进行计算,才能给出正确的结论. ) [1] Zhang P W, Wu H P, Wang B. Time-harmonic P-waves engulfing a rectangular limited-permeable crack in piezoelectric medium: energy density and energy release [J].TheoreticalandAppliedFractureMechanics, 2011,59(3): 169-184. [2] Zhao X H, Meguid S A. On the dynamic behaviour of a piezoelectric laminate with multiple interfacial collinear cracks [J].InternationalJournalofSolidsandStructures, 2002,39(9): 2477-2494. [3] Liu F, Zhong X C. Transient response of two collinear dielectric cracks in a piezoelectric solid under inplane impacts [J].AppliedMathematicsandComputation, 2010,217(8): 3779-3791. [4] Hao T H, Shen Z Y. A new electric boundary-condition of electric fracture-mechanics and its applications [J].EngineeringFractureMechanics, 1994,47(6): 793-802. [5] Hao T H. Multiple collinear cracks in a piezoelectric material [J].InternationalJournalofSolidsandStructures, 2001,38(50/51): 9201-9208. [6] Ding H J, Chen B, Liang J. General solutions for coupled equations for piezoelectric media [J].InternationalJournalofSolidsandStructures, 1996,33(16): 2283-2298. [7] Yang F Q. Fracture mechanics for a Mode Ⅰ crack in piezoelectric materials [J].InternationalJournalofSolidsandStructures, 2001,38(21): 3813-3830. [8] Gradshteyn I S, Ryzhik I M.Tableofintegral,seriesandproducts[M]. New York: Academic Press, 1980. [9] Erdelyi A.TablesofIntegralTransforms[M]. New York: McGraw-Hill, 1954. [10] Morse P M, Feshbach H.MethodsofTheoreticalPhysics[M]. New York: McGraw-Hill, 1958. [11] Itou S. 3-Dimensional wave-propagation in a cracked elastic solid [J].JournalofAppliedMechanics,ASME, 1978,45(4): 807-811. [12] Zhang P W, Zhou Z G, Wu L Z. Coupled field state around three parallel non-symmetric cracks in a piezoelectric/piezomagnetic material plane [J].ArchiveofAppliedMechanics, 2009,79(10): 965-979. [13] Zhang P W, Zhou Z G, Li G. Q. Interaction of four parallel non-symmetric permeable mode-Ⅲ cracks with different lengths in a functionally graded piezoelectric material plane [J].ZeitschriftfürAngewandteMathematikundMechanik, 2009,89(9): 767-788. (in Russian) [14] Itou S. Three-dimensional dynamic stress intensity factors around two parallel square cracks in an infinite elastic medium subjected to a time-harmonic stress wave [J].ActaMechanica, 2000,143(1/2): 79-90. [15] Itou S. 3D dynamic stress intensity factors at three rectangular cracks in an infinite elastic medium subjected to a time-harmonic stress wave [J].ArchiveofAppliedMechanics, 1999,69(4): 286-298.
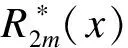
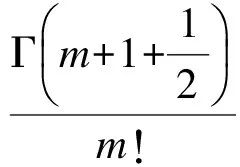
3.2 能量释放率
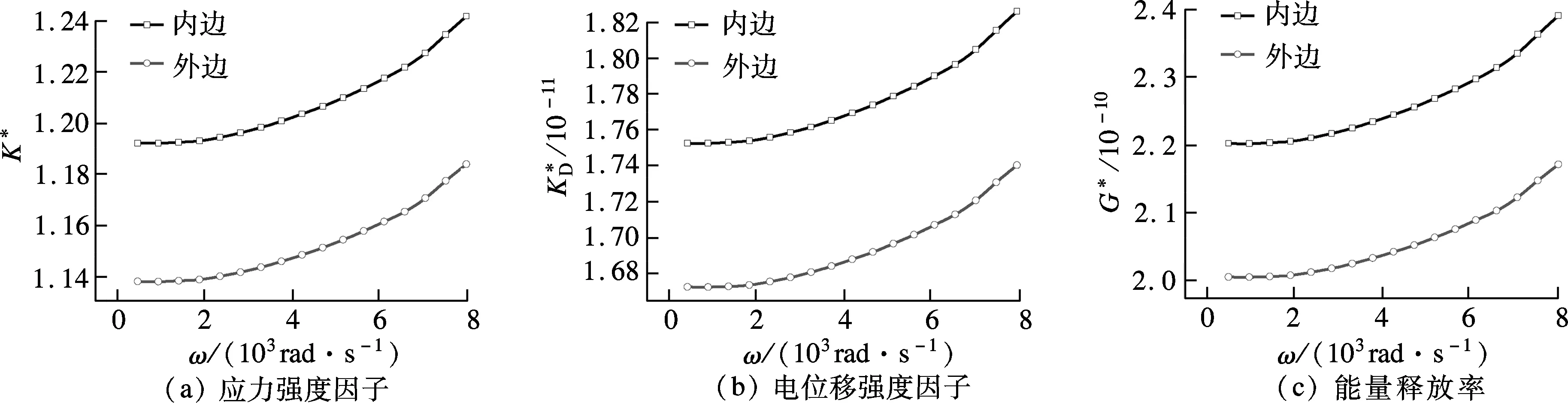
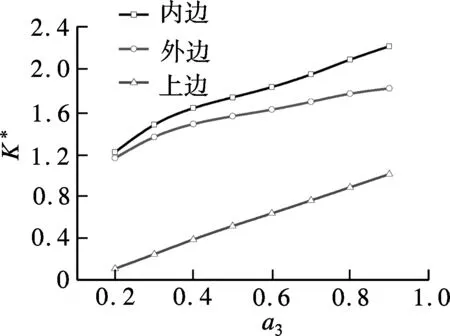
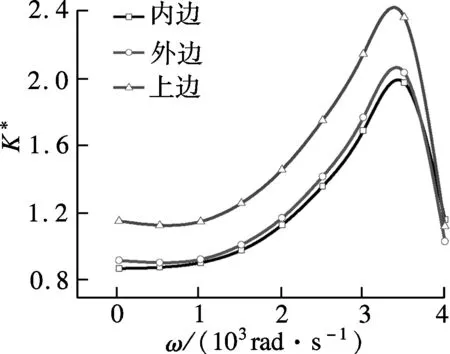
4 数值计算结果及讨论








5 结语
