大跨钢桥钢箱梁损伤时变模型及疲劳可靠性评估

王 莹 李兆霞 赵丽华

(东南大学土木工程学院, 南京 210096)(东南大学江苏省工程力学分析重点实验室, 南京 210096)

随着结构健康监测系统在大跨斜拉桥上的应用,传统的有限元模型已无法满足健康监测和疲劳损伤评估的需要,结构整体和局部细节特性的表征需要借助于多尺度有限元模型[1-3]．同时,结构在长期服役过程中产生的损伤、焊趾裂纹都应该在模型中及时更新,以反映结构当前的时变损伤状态,才能使用于结构疲劳评估的模型分析结果准确反映结构中的热点应力分布状态．大跨斜拉桥索梁锚固区作为斜拉索与钢箱梁之间的连接区域,其焊缝众多,受力复杂[4-5],运营荷载下的疲劳问题十分突出．然而,健康监测系统中的传感器无法获取该处的热点应力分布,需要借助于有效的有限元仿真技术来进行该处热点应力的模拟[6-7]．

本文以润扬长江公路大桥北汊斜拉桥索梁锚固区焊接细节为分析对象,建立了包括桥梁整体结构、索梁锚固区构件、焊缝及其焊接细节处假定的表面裂纹的多尺度有限元模型,借助人工检测获得的损伤信息来更新桥梁在服役不同时期的有限元模型,以实时反映桥梁在当前服役状态下的损伤状态和应力水平．对该桥在重型车辆荷载作用下的索梁锚固区局部应力进行分析,基于焊接处的表面裂纹和断裂力学方法评估了索梁锚固区假定的表面裂纹对整体结构疲劳状态的影响、应力分布以及断裂疲劳寿命．考虑无损探测信息,实现了钢箱梁关键构件疲劳可靠度的更新．

1 考虑损伤时变状态的桥梁模型更新方法

桥梁的疲劳损伤累积是一个长期的时变演化过程,交通管理部门每年都会对其进行分段人工检测,以获得实际出现在桥梁上的缺陷信息．若要得到实际桥梁结构在各个运营时段准确的损伤状态,仅通过一个面向结构疲劳寿命与可靠度评估的初始有限元模型是不可能实现的,必须借助于人工检测信息，不断更新桥梁在服役不同时期的有限元模型,以实时反映桥梁在当前服役状态下的损伤状态和应力水平．本文在桥梁整体粗糙模型的基础上,建立了包含等效正交异性桥面板的局部钢箱梁模型．对易于出现疲劳裂纹的索梁锚固区域,假定经过长期服役和疲劳损伤累积以后出现了疲劳裂纹,估算了桥梁结构的疲劳裂纹扩展寿命．建模及考虑损伤时变状态进行模型更新的流程如图1所示．

以润扬北汊斜拉桥为例,概述模型建立的过程和要点．润扬长江大桥北汊斜拉桥为双塔三跨双索面斜拉桥,跨径布置为175.4m+406m+175.4m,为全封闭双向六车道的高速公路桥．首先根据设计图,建立桥塔、拉索和主梁模型,主梁先采用鱼骨梁模型进行简化,得到结构整体模型(单元特征尺度量级为100m).经过参数修正,使其动力特性与实测值吻合较好[3],为进一步模拟结构中的易损局部和考虑局部损伤时变状态进行模型更新提供了前提条件．然后,在整体粗糙有限元模型的基础上,建立了跨中段的钢箱梁精细有限元模型(单元特征尺度量级为10-3m)．考察桥梁影响线,所建立的钢箱梁精细模型的跨径为146m,以便于进行锚固区疲劳应力的分析．

图1 建模与考虑损伤时变进行模型更新的流程示意图

在钢箱梁精细模型的基础上,对于索梁锚固区,建立更为精确的焊缝单元,其构造如图2所示．

图2 润扬斜拉桥整体和局部有限元模型

承压板N2的焊缝属性通过改变焊缝处壳单元的厚度来模拟,底板及承压板N1的焊缝单元属性则通过梁单元来模拟．焊缝厚度的模拟依据润扬斜拉桥实际的焊接工艺,结合规范确定．

结构焊缝的焊趾附近为裂纹易发的危险区,文献[8]调研资料显示,沿桥梁纵向的裂纹最为常见．考虑桥梁运营初期的浅表裂纹,设定承压板N1为考察对象,建立深度为2mm的表面纵向裂纹模型,考虑上述疲劳裂纹状态对模型相关局部进行更新,更新后的局部模型如图3示．图中,A表示承压板裂纹区域;B表示裂纹尖端区域,且在区域B中最里侧单元类型为奇异单元Solid95．

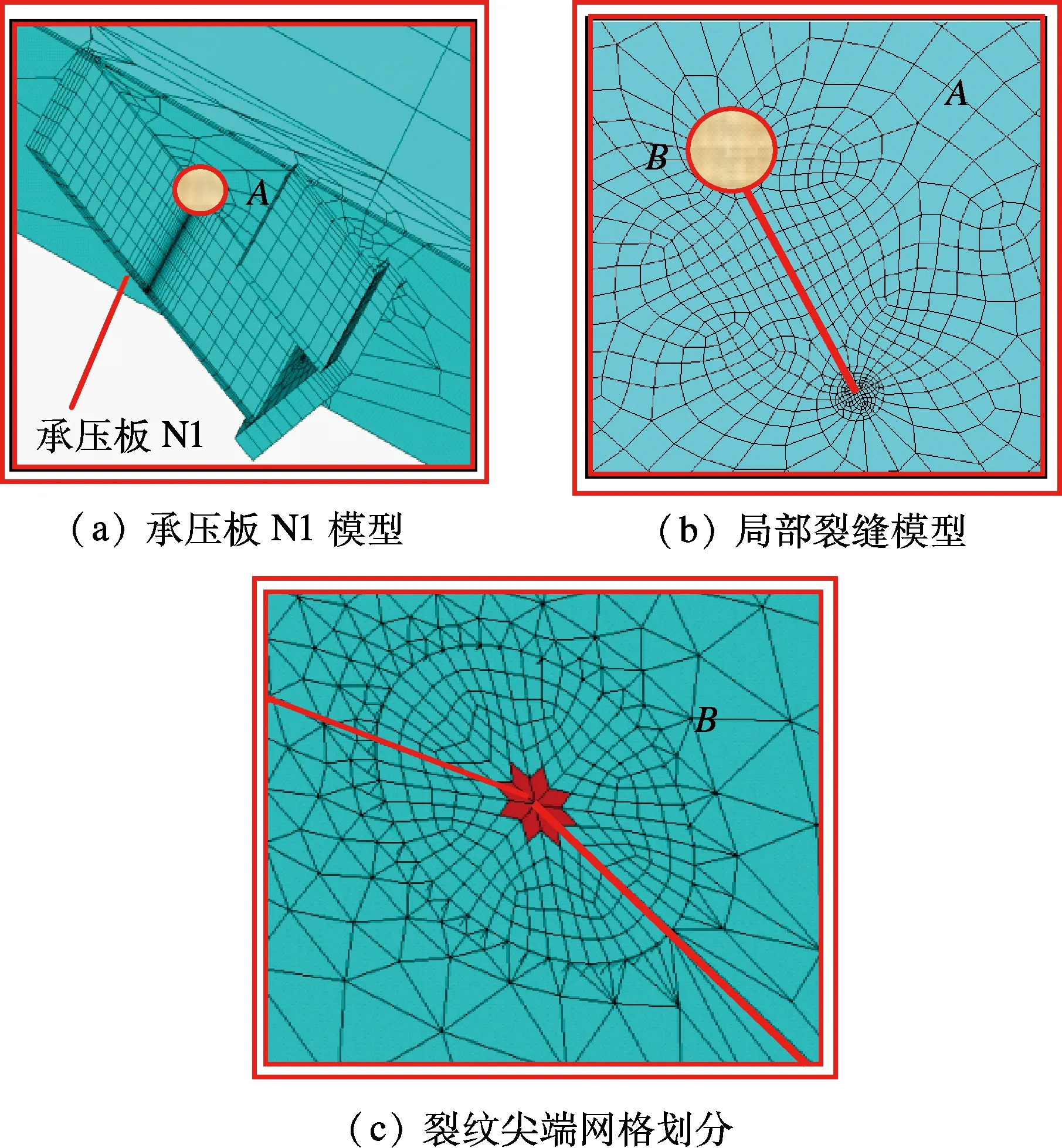
图3 考虑疲劳裂纹状态的局部模型更新示意图

2 润扬大桥索梁锚固区疲劳状态评估

利用第1节建立的模型,可进行梁锚固区的应力响应分析和疲劳状态评估．

2.1 基于Miner累积损伤定律的疲劳状态评估

英国规范BS 5400[9]是最早给出桥梁疲劳设计的标准疲劳车模型及其计算方法的规范,忽略总重小于30kN的典型车辆对桥梁构件疲劳损伤的影响,用一辆总重320kN的4轴虚拟“标准疲劳车”来表示典型车辆标准载荷频值谱效应．借鉴该“标准疲劳车”来进行移动车载加载．所得跨中截面附近箱梁构件的典型应力时程曲线如图 4所示．由图可知,车辆移动载荷在跨中附近会引起2个大小相近的低于15MPa的循环应力幅值．基于该应力幅值,采用Miner累积损伤定律,初步得到桥梁关键钢箱梁构件和拉索构件的疲劳寿命．

图4 跨中钢箱梁构件的典型应力时程

由于ANSYS软件中的时间历程后处理器Timehist Postpro每次只能导出单个节点的应力时程,为了直观显示出变幅荷载作用下所有位置处的应力时程和相应的疲劳寿命,采用如下步骤即可实现桥梁所有位置处构件疲劳寿命的可视化:

① 将车辆荷载作用静力移动荷载施加于润扬大桥的钢箱梁节点上,所施加载荷步的步数依赖于求解的精度和运算速度,每个加载步即对应标准疲劳车行驶至箱梁跨长方向的不同位置．

② 利用ANSYS软件中的时间历程后处理器Timehist Postpro,将所有位置处的应力时程数据以.txt的格式导出并存储．

③ 在MATLAB程序中对所有.txt格式的应力时程数据进行雨流计数,得到所有位置处的雨流计数结果,即应力谱．

④ 计算所有位置处的等效应力幅值Δσef,即

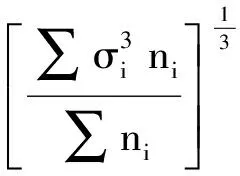
(1)

式中,σi为雨流计数得到的第i级应力幅;ni为σi对应的循环次数．该等效应力幅值所引起的疲劳寿命等于变幅荷载作用所引起的疲劳寿命．

⑤ 利用Miner定律计算累积损伤值D,即

(2)

式中,C为对应材料S-N曲线的参数,其中,S为材料所承受的应力幅值,N为该应力幅值下的疲劳寿命．在MATLAB程序中利用Save命令将所有位置处疲劳寿命以.txt的格式存储,命令为Save Nodelife.txt-ASCII N．

⑥ 在ANSYS软件中,利用*VREAD命令,读取步骤⑤得到的所有位置处疲劳寿命的.txt文件．

⑦ 利用宏命令*DNSOL命令将导入的后缀为.txt的数据赋值给相应的节点,以实现所有位置处疲劳寿命的可视化．大跨钢桥钢箱梁构件的疲劳寿命如图5所示．由图可见,索塔附近的疲劳寿命较长,边跨和跨中处的疲劳寿命相对较短,故下面以跨中处的索梁锚固区作为研究对象,研究其出现疲劳裂纹时的疲劳寿命和相应的疲劳可靠性．

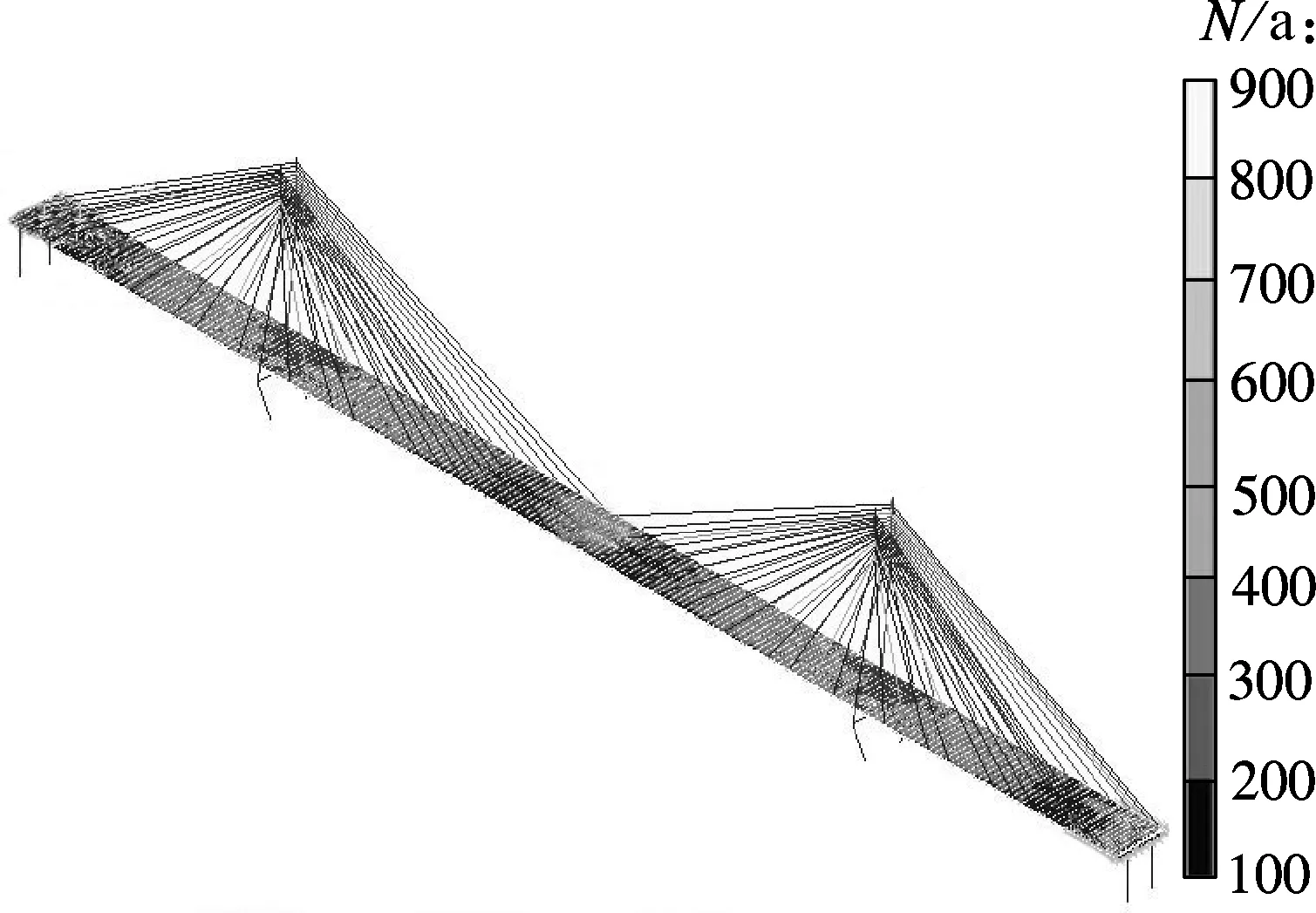
图5 润扬斜拉桥关键构件的疲劳寿命值

2.2 裂纹扩展导致的钢箱梁构件疲劳状态评估

假设考察部位在运营若干年后出现了裂纹,建立了0.1mm缝宽下裂纹长度分别占承压板总长1.33%,2.00%,2.67%,3.33%,4.00%,5.33%,6.67%,10.00%时的一系列裂纹．裂纹尖端均采用Solid95单元,该单元可模拟裂纹尖端的奇异性．

2.2.1 应力场分布

当裂纹长度占承压板总长5.33%、裂缝宽度为0.1mm时,裂纹尖端的应力分布状况如图6所示．由图可知,裂纹尖端出现了应力集中现象,表现出应力奇异性．

图6 裂纹区域及其尖端应力场分布图

2.2.2 不同裂纹长度下的K值

当裂纹缝宽w=0.1mm时,不同长度的初始裂纹对应的应力强度因子K如图7所示．图中,l表示裂纹长度占承压板总长的百分数．由图可知,K随着初始裂纹长度的增加而增加．当l≤6.67%时,K值增加较快;当l>6.67%时,K值增加速度变慢．根据图7,可拟合得到不同裂纹尺寸对应的应力强度因子K的计算公式,即

K=0.0011l3-0.1131l2+5.8470l-11.0028

(3)

图7 不同裂缝长度的K值(w=0.1mm)

2.2.3 疲劳寿命评估

依据断裂力学Paris公式,可得到裂纹由初始长度ai扩展到t时刻的长度时at的疲劳寿命为

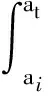
(4)

式中,P,m为裂纹扩展参数,此处根据规范BS 7910[10],P=2.18×10-13,m=3;ΔK为根据式(1)计算得到的等效应力幅Δσef作用下具有不同初始裂纹尺寸的裂尖的应力强度因子幅值,该值基于疲劳加载的多尺度模型,由拟合式(3)计算得到;a为瞬时裂纹长度．当裂纹扩展到贯穿承压板时,认为构件失效,此时破坏的裂纹长度af=69.95cm,由此可得各裂纹长度下构件的荷载作用次数Nf．参考规范BS 5400中给定的每年交通荷载通过的频次,可得各裂纹长度下构件的疲劳寿命,结果见图8．可以看出，当l≤5.33%时，疲劳寿命较高，但随着裂纹长度的增加，寿命迅速降低；当l>5.33%时，随着裂纹的增加，疲劳寿命降低并趋于平缓，但此时疲劳寿命值很小.由此表明，在人工检测和无损探伤领域，初始裂纹长度达到承压板总长5%的疲劳裂纹应该列入当前检修计划内.

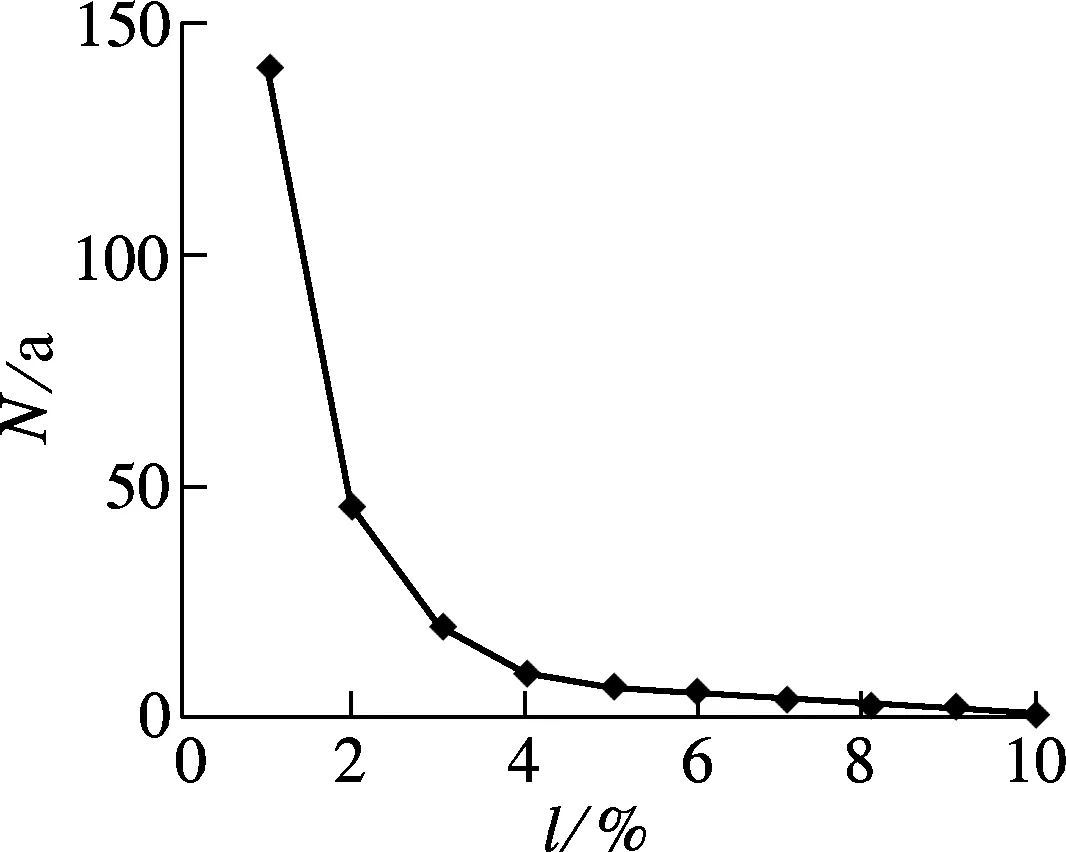
图8 疲劳寿命随初始裂纹长度的变化曲线

3 基于无损探测信息的钢箱梁构件疲劳可靠性更新

在概率断裂力学方法中,分析钢桥的疲劳可靠性时,通常考虑在指定时间t内初始裂纹ai扩展到at;当at大于临界裂纹尺寸acr时,即可认为发生疲劳失效,则钢桥疲劳裂纹随机扩展的极限方程为

Z=acr-at

(5)

临界裂纹尺寸acr是指超过此尺寸就会发生断裂破坏或不适合继续承受荷载作用,通常使用K准则或适合承载条件准则来判定．

使用K准则时,认为acr与材料断裂韧度KIC直接相关,可表示为

(6)

式中,F(a)=2.3512为几何形状修正系数;σ为远离裂纹的名义应力或应力幅．对于Q345型钢材,KIC≈95MPa·m1/2．

使用适合承载条件准则时,临界裂纹尺寸acr被定义为一个明确的裂纹尺寸．若板件中的裂纹大于acr时，细节将不能满足使用性要求．通常来说,适合承载条件准则比K准则所定义的临界裂纹尺寸更保守．

由式(6)可见,at在积分号的上限,根据数值积分法,at无法显式表示,因此需要设定不同的服役年限来反推at．根据工程经验,认为at,acr均服从对数正态分布,考虑到焊接细节,将其变异系数取为0.5．

通过编制Monte-Carlo程序,可以得到当索梁锚固区内初始裂纹长度达到承压板总长的1%时,不同服役年限对应的疲劳可靠度指标，结果见图9．

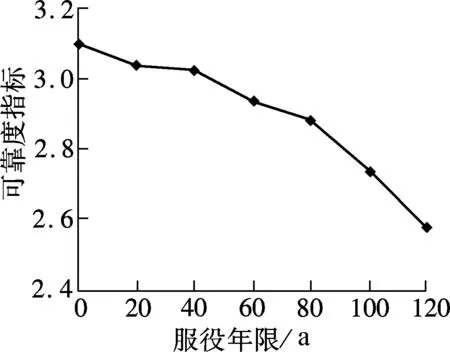
图9 不同服役期的可靠度指标(l=1%)

桥梁管理部门定期会对桥梁进行人工检测或无损探伤,如何在可靠度模型中引入这些检测信息是目前研究的热点．由于检测技术和水平的限制,在检测过程中通常存在以下3种结果:① 检测到具体的裂纹尺寸;② 存在裂纹,但由于检测水平有限并没有被检测到;③ 检测到了裂纹,由于检测水平差异,无法准确获得具体尺寸．相应的状态函数方程也可分为以下3种[11]．

1) 检测到具体裂纹尺寸时,对应的极限状态方程为aN0-Q=0,即检测到的裂纹长度尺寸aN0等于真实的裂纹长度尺寸Q．构件失效的极限状态方程表示为

Z=acr-aN0≤0

(7)

此时的失效概率应为条件概率,即检测到具体裂纹尺寸且该尺寸达到临界裂纹尺寸时的条件概率．该失效概率可以表示为

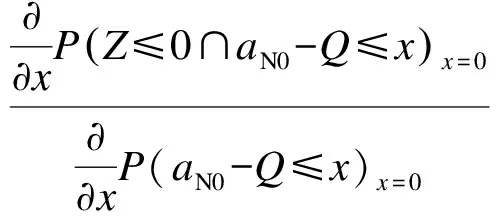
(8)

式中，βup为更新后的可靠度指标.

由于定值处无法求解条件概率的值,故将条件aN0-Q=0设置为-x≤aN0-Q≤x,此时x取为很小的值,假设为x=0.002,则该失效概率的求解步骤如下:

① 计算P(Z≤0∩aN0-Q≤-0.002)及P(aN0-Q≤-0.002);

② 计算P(Z≤0∩aN0-Q≤0.002)及P(aN0-Q≤0.002);

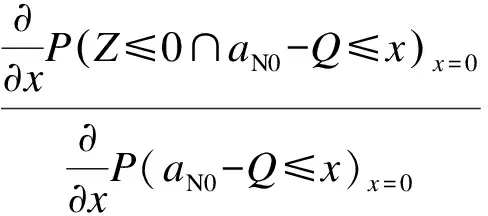
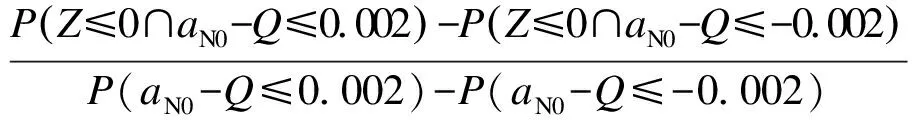
2) 裂纹存在,但由于检测水平有限并没有被检测到时,相应的状态方程可表示为

Z1=aN0-ad≤0

(9)

式中,ad表示可探测到的裂纹的最小尺寸．此时更新的失效概率可表示为

(10)

式中,Z1取决于无损检测的裂纹检测概率,通常由POD曲线来确定.服从指数分布的POD模型的计算公式如下:

POD(a)=(1-p)(1-e-ca)

(11)

式中,p为裂纹尺寸a的置信参数,取值范围通常为[0.01,0.05];c为根据试验数据得到的参数,取值范围通常为[100,500]．可以看出,裂纹尺寸越大,相应的检测概率POD值越大．由此可得

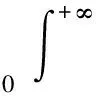
(12)

式中,faN0(a)为裂纹尺寸概率密度函数．由此可以推导出更新的失效概率为

(13)

3) 检测到裂纹但其尺寸未知时,相应的状态方程可以表示为

Z2=aN0-ad≤0

(14)

此时更新的概率可以表示为

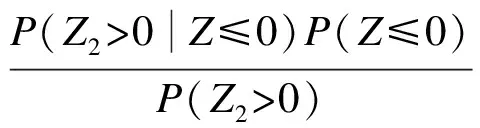
(15)

假设索梁锚固区的初始裂纹为承压板长度的3%,即45mm．使用适合承载条件准则时,假定当临界裂纹尺寸acr达到承压板长度的10%时,不能满足使用性要求,即临界裂纹取为150mm．假定大跨钢桥的目标可靠度为2.0,通过编制Monte-Carlo程序,可以得到l=3%时结构不同服役期的疲劳可靠度指标(见图10)．由图可知,当桥梁服役8年后,由该初始裂纹扩展得到的可靠度低于目标可靠度,需要对承压板进行维修或者更换．

图10 结构的可靠度指标(l=1%)

在第8年检测到具体裂纹时,实际裂纹尺寸服从以均值为检测值Am、变异系数为0.25的对数正态分布．假定裂纹检测值L的取值范围为(0.1±0.002)mm,利用式(9)可以得到更新的可靠度曲线(见图11)．由图可知,检测到具体裂纹后,可靠度指标显著增加．随着服役年限的增加,可靠度指标迅速下降,并向更新前的可靠度指标靠拢．根据更新后的可靠度指标与目标可靠度的比较结果可知,当检测到裂纹后,相应的检修周期可以推后．

图11 第8年检测到的具体裂纹的可靠度

没有检测到裂纹时,考虑裂纹检测的POD模型,c∈[100,500],p∈[0.01,0.05],可以得到更新后的可靠度曲线(见图12)．由图可知,c值对可靠度指标有较大影响;p值对可靠度指标起反作用,p值越大,可靠度指标越低．此外,第8年未探测到裂纹时,由于可靠度指标得到了提高,相应的检修时间可以延后．

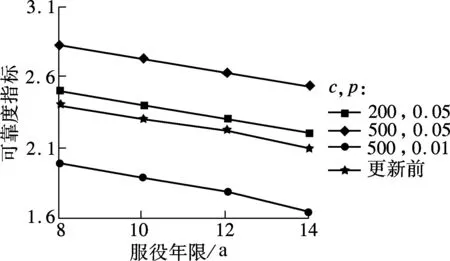
图12 未检测到裂纹时的可靠度曲线

检测到裂纹但具体裂纹尺寸未知时,考虑检测概率的POD模型,得到在第8年被检测到但具体长度未知裂纹(l=3%)时结构的可靠度曲线(见图13)．由图可知,更新后的可靠度水平普遍降低,需要对构件进行再次检测．

图13 检测到未知裂纹时的可靠度曲线

4 结论

1) 考虑损伤时变状态对结构中复杂易损部位进行模型更新,对于获得结构由于当前损伤状态导致的复杂应力分布和准确的疲劳状态评估是十分必要的,这为含裂纹的桥梁结构的疲劳状态评定提供了一种精确的分析手段．

2) 裂缝宽度相同时,应力强度因子随裂纹长度的增加而增大．当裂纹长度处于承压板总长的5.33%以内时,疲劳寿命高,但随着裂纹长度的增加,寿命迅速降低;当裂纹长度超过承压板总长的5.33%时,随着裂纹的增加,疲劳寿命降低并趋于平缓,但此时疲劳寿命值很小．此结果验证了在人工检测和无损探伤领域,初始裂纹长度达到承压板总长5%的疲劳裂纹应该列入当前检修计划内的结论．而低于承压板总长5%的裂纹可以依据需要暂时不予以维修．断裂力学理论认为,初始裂纹对疲劳寿命影响很大,这一结论在本文中也得到验证．

3) 无损检测时检测到的裂纹尺寸可用于模型更新和疲劳损伤可靠度更新．根据更新后的可靠度指标与目标可靠度的比较结果可知,在无损检测中,当检测到具体的裂纹尺寸后,相应的检修周期可以推后．若未检测到裂纹,则更新后的结构可靠度指标提高,此时也可以将结构的检修周期延长．若检测到裂纹但裂纹的长度未知,则根据此裂纹信息对结构进行更新,整个结构的可靠度指标降低,此时需要对构件进行再次检修．

)

[1] Li Z X. Concurrent multi-scale modeling of civil infrastructures for analyses on structural deteriorating.Part Ⅰ: modeling methodology and strategy[J].FiniteElementinAnalysisandDesign, 2009,45(11): 782-794.

[2] Wang Y, Li Z X, Wang C M. Concurrent multifactor optimisation techniques for model updating of long-span bridges[J].StructureandInfrastructureEngineering, 2013,9(6): 578-593.

[3] 孙正华, 李兆霞, 陈鸿天.结构行为一致多尺度有限元模型修正及验证[J]. 东南大学学报:自然科学版, 2009, 39(1): 85-90.

Sun Zhenghua, Li Zhaoxia, Chen Hongtian. Updating and verification for multi-scale finite element model of structure behavior [J].JournalofSoutheastUniversity:NaturalScienceEdition, 2009,39(1): 85-90. (in Chinese)

[4] Liu Xiumin, Chen Congxin, Zhen Yun. Stability and failure mechanism of tunnel anchorage for suspension bridge [J].DisasterAdvances,2012,5(1): 181-186.

[5] Timosidis D, Pantazopoulou S J. Anchorage of longitudinal column reinforcement in bridge monolithic connections [J].JournalofStructuralEngineering，ASCE, 2009,135(4): 344-355.

[6] 瞿伟廉, 何杰, 王文利.基于子模型法的钢桁桥整体节点动力相应分析[J]. 地震工程与工程振动,2009, 29(3): 95-100.

Zhai Weilian, He Jie, Wang Wenli. Dynamic stress analysis of monolithic joint of steel truss bridge based on submodel method [J].JournalofEarthquakeEngineeringandEngineeringVibration, 2009,29(3): 95-100.(in Chinese)

[7] Chan T H T. Hot spot stress approach for Tsing Ma Bridge fatigue evaluation under traffic using finite element method [J].StructuralEngineeringandMechanics, 2005,19(3): 261-279.

[8] 赵建华. 断裂力学在桥梁裂纹检测分析中的应用[D]. 西安: 长安大学工程力学学院, 2008.

[9] BSI. BS 5400 Code of practice for fatigue[EB/OL]. (1982-03)[2012-04-08]. http://zh.scribd.com/doc/64041770/BS5400-10-1980-Code-of-Practice-for-Fatigue.

[10] BSI. BS 7910 Guide to methods for assessing the acceptability of flaws in metallic structures[EB/OL]. (2005-07)[2012-04-08]. http://shop.bsigroup.com/ProductDetail/?pid=000000000030164728.

[11] 王春生, 刘鑫, 俞欣, 等. 基于无损探测信息的既有钢桥构件疲劳可靠度更新评估[J]. 土木工程学报， 2010, 43(8): 81-87.

Wang Chunsheng, Liu Xin, Yu Xin, et al. Fatigue reliability updating evaluation using nondestructive inspections for existing steel bridges[J].ChinaCivilEngineeringJournal, 2010,43(8): 81-87. (in Chinese)