考虑时滞效应的龙爪槐树干液流人工神经网络模型研究

谢恒星，张振华

（1.渭南师范学院 陕西省多河流湿地生态环境重点实验室，陕西 渭南714000；2.鲁东大学地理与规划学院，山东 烟台 264025）

考虑时滞效应的龙爪槐树干液流人工神经网络模型研究

谢恒星1,2，张振华2

（1.渭南师范学院 陕西省多河流湿地生态环境重点实验室，陕西 渭南714000；2.鲁东大学地理与规划学院，山东 烟台 264025）

以鲁东大学校内5年生龙爪槐为例，分别利用美国产AZ-M茎流系统和澳大利亚产AXWG03自动气象站对植株的树干液流和微环境气象因子进行了观测，探讨了BP-人工神经网络模型在植物液流与环境因子定量分析中的适用性，并比较了考虑液流相对于微环境气象因子滞后效应前后人工神经网络模型拟合精度的变化。结果表明，树干液流速率相对于太阳总辐射、光合有效辐射和风速分别存在10 min、10 min和20 min等间隔不等的时滞。与传统的多元线性回归和不考虑滞后效应的BP-人工神经网络模型相比，考虑滞后效应的人工神经网络模型的拟合精度显著提高，考虑、不考虑滞后效应的人工神经网络模型和多元线性回归模型得到的液流速率拟合值与观测值回归方程的决定系数分别为0.94 4、0.888和0.853；液流速率拟合值与观测值相对误差处于±5%和±10%范围内的分别为41.177%、35.849%、30.189%和70.588%、62.264%、31.527%。由分析结果可知，液流的时滞是模型建立中一个不可忽略的现象。

龙爪槐；BP-人工神经网络；多元线性回归；拟合精度；滞后效应

植物蒸腾在SPAC系统水热传输中占有重要的地位，一直是农学、林学、气象学、生态学等众多学科共同关注的热点问题之一[1]。测量植株蒸腾的方法很多[2]，其中的热技术方法(主要用于高大乔木)由于具有基本不破坏树木正常生长状态、连续观测、易于野外操作等优点而得到了广泛应用。热技术根据不同的原理可分为热脉冲法、热平衡法和热扩散法[3]。国内外许多科研工作者应用热技术对植株液流进行了研究，如刘奉觉、Dawson等分别应用热脉冲技术研究了杨树树干液流的时空动态和糖槭大树与小树水分利用量的差异[4-5]；严昌荣、Martin等分别应用热平衡技术研究了北京山区落叶阔叶林中核桃楸在生长中期的树干液流和冬季火炬松、湿地松人工林树干液流的变化[6-7]；孟平、Kostner等分别应用热扩散技术测算了苹果树树干液流数据，分析了苹果树蒸腾耗水规律及其与微气象要素之间的关系和不同处理条件下欧洲赤松的单位边材面积最大液流量[1,8]。植株液流受环境因子的强烈影响，但影响液流的环境因子错综复杂，各环境因子之间存在较强的相关性，它们对液流的影响往往是非线性的[4,6,8]。国外在模型探讨方面所作工作相对较多[9-12]，但由于树木本身的水容调节作用和水分从树木根部运移到叶片需要一段时间[13-14]，树干液流相对于环境因子往往存在滞后效应，而很多研究者没有考虑到这个问题[11]。人工神经网络是一个具有高度非线性的超大规模连续时间动力系统，因其具有自学习功能、联想存贮功能、高速寻找优化解功能等优点而在经济、化工、水文、农业等领域得到了广泛应用[15-18]，但其在液流与环境因子关系分析方面研究还相对较少。本文尝试利用BP-人工神经网络模型建立树干液流与环境因子的定量关系，并比较考虑滞后效应前后人工神经网络模型精度的变化，以期精确揭示液流与环境因子的定量关系。

1 材料与方法

1.1 研究区概况

实验于2005～2007年在鲁东大学校内龙爪槐人工林内进行，人工林面积约为630 m2，株、行距为2.5 m，所植龙爪槐为5龄。试验地地理位置为 37°14′N，121°27′E，海拔 63 m。年均气温11.8℃，年均风速4～6 m/s，多年平均降雨量651.9 mm，年均相对湿度68%，年均日照时数2 698.4 h，无霜期 210 d，属暖温带大陆性季风气候。土壤属烟台市典型棕壤，土层厚度3 m左右，根系活动层平均土壤pH值6.7，有机质含量14.23 mg/kg，全 N1.09 mg/kg，速效 P11.42 mg/kg，土壤容重1.42 g/cm，地下水位2～3 m。研究期间植物水分和肥料供应充足。

1.2 仪器安装

选择长势良好，树干通直，树皮光滑，冠幅、高度相似的3株龙爪槐作为被测树木，以3株样木的平均液流速率作为树干液流速率。样木的平均胸径、株高、冠幅分别为5.2 cm 、2.7 m和2.5 m×2.3 m。在距离地面130 cm处分别安装美国DYNAMAX公司产AZ-M茎流系统的SGB50探头，以避免近地面冷液流的影响[19]。在光滑的茎段上用小刀将树干外的死树皮刮去，再用细砂纸将其打磨光滑，涂上一层很薄的硅胶树脂（G4型），防止水分顺树干进入测定部分或者水气的液化，保护探头不受损伤和防止与树干粘连[6]，然后用O形环将探头的上下两头密封严实。为了防止太阳辐射对探头的影响，在安装好探头后再在探头的外层包裹上3层铝箔。探头通过SF2-135数据转换器与数据采集器（CHANNEL DATA LOGGER）连接，利用12 V铅蓄电池给数据采集器供电。在距样木3 m的空地上安置澳大利亚PTY公司产AXWG03自动气象站，自动气象站可同步观测气温x1（℃）、太阳总辐射量x2（w/m2）、x3风速（m/s）、相对湿度 x4（%）和光合有效辐射量 x5（μmol/(m2·s)）等气象因子。自动气象站和茎流计数据采样间隔均为15 s，每10 min进行平均值计算并记录下来。由于晴天的液流数据更有代表性[1,4,8]，因此选取8月19、20、21日3个晴天白天同时刻的平均液流、气象数据作为分析对象，并用8月22日的气象、液流数据进行模型检验。

2 结果与分析

2.1 人工神经网络模型的基本原理

一个三层的BP人工神经网络模型能够实现任意的连续映射，三层BP网络模型如图1所示。 图中wij表示输入层第i个神经元与隐含层第j个神经元之间的连接权值，vjk表示隐含层第j个神经元与输出层第k个神经元之间的连接权值。设隐含层第j个神经元的阈值为θj，输出层第k个神经元的阈值为γk，则隐含层第j个神经元的输入为[20]。

式中，xi为输入层第i个神经元的输入值；n为输入层的神经元个数。

输出为

图1 三层 BP 人工神经网络Fig.1 Three layer BP artif i cial neural network

式中，p为隐含层神经元个数，f为激励函数，其形式为

输出为

计算过程中，隐含层神经元的激励函数取为S型，而输出层神经元的激励函数取为线性型。为了提高网络的性能，减少其陷入局部极小值的可能性，提高收敛速度，通常采用改进的BP算法—动量法来实现，即

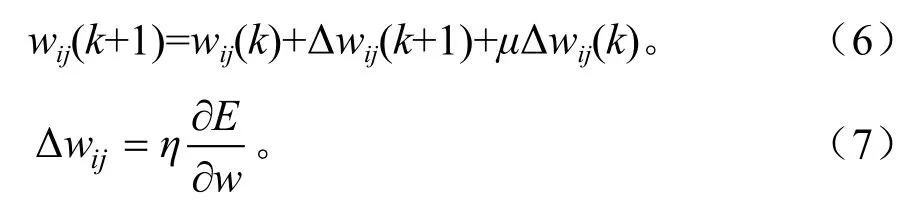
其作用是模拟生物神经元的非线性特性。

输出层第k个神经元的输入为

式中，μ为动量因子；η为比例系数，在训练中反映了学习速率，且η∈(0,1)；E为误差函数。

时刻t网络的误差函数定义为

式中，yk(t)为输出层第k个神经元在时刻t的实际输出，dk(t)为该时刻的希望输出，q为输出层的神经元数。

当E(t)≤ε(ε为预先给定的误差)时，网络停止训练，此时的网络模型就是所需要的。

2.2 树干液流人工神经网络模型分析

对于本树干液流人工神经网络模型来说，输入神经元为环境因子，输出神经元为蒸腾速率。在DPS6.55数据处理软件“BP神经网络分析参数设置”对话框中，隐含网络层数、输入层节点数、最小训练速率、动态参数、参数SΙGMOΙD、允许误差和最大迭代次数分别设置为“3”、“5”、“0.1”、“0.6”、“0.9”、“0.000 1”和“1 000”。由于原始数据量纲不同和数值存在数量级的明显差异，首先要对原始数据进行标准化处理。系统经过755次计算，2次迭代结果的误差小于0.000 1，迭代收敛，结束计算，确定隐含层节点数为5。该模型输入层各神经元与隐含层各神经元的连接权值、隐含层各神经元与输出层各神经元的连接权值如表 1、2。

表1 输入层各神经元与隐含层各神经元之间的连接权值WijTable 1 Connecting weight values between input and invisible layer neural cells

表2 隐含层各神经元与输出层各神经元之间的连接权值VjtTable 2 Connecting weight values between invisible and output layer neural cells

2.3 模型精度对比分析

利用BP人工神经网络模型计算得到液流速率的拟合值，利用拟合值与观测值建立回归方程，二者之间的散点图如图2。

图2 人工神经网络拟合结果Fig.2 Fitted rusult of artif i cial neural network model

由图可知，拟合值与观测值回归方程的决定系数为0.888，拟合值与观测值的相对误差处于± 5%和±10%之间的分别为30.189%和 31.527%，模型拟合精度较高。液流值较大时拟合值偏离回归线较大，这可能是因为液流最大值出现在中午前后[1,19]，而午间叶片经常出现光合“午休”现象而导致叶片气孔关闭[19]，此时液流将不随气温或辐射的增加而增大，从而导致模型拟合精度的降低。为了对比所建立的人工神经网络模型的拟合精度，利用环境因子与液流速率进行多元线性回归，得到回归方程为：

y=-10349.405+482.094x1+13.801x2+46.499x3-2.663x4-4821.709x5R2=0.853 （9）

由方程可知，回归方程的决定系数为0.853，液流速率拟合值与观测值的相对误差处于 ± 5%和±10%之间的分别为35.849%和62.264%，方程的拟合精度较高，与BP人工神经网络模型相比，拟合精度稍微降低。当液流速率较大时，方程的拟合值与观测值的偏差同样较大（图3）。由回归系数可知，影响液流的主要因素为光合有效辐射。孟平等提出影响苹果树蒸腾的主要因素是净辐射[1]，这是因为净辐射是该作者监测的唯一辐射指标。虽然多元线性回归方程可以拟合环境因子与液流的数量关系，但多元线性回归是以自变量相关性较弱为前提，当自变量间相关程度较高时，建立多元线性回归的最小二乘法可能失效，模型将失去意义[21]。由表3可知，气温和太阳辐射、相对湿度及光合有效辐射之间存在很强的相关性，因此利用多元线性回归建立液流与环境因子之间的定量关系的有效性还有待于进一步探讨。

图3 多元线性回归拟合结果Fig.3 Fitted result of multiple linear regression model

表3 自变量间相关系数Table 3 Correlation coefficients between independents

2.4 考虑液流时滞效应的人工神经网络模型

由于枝干的水容调节，液流相对于环境因子存在不同程度的时滞，这种时滞的存在往往被许多研究者所忽略[11,22]。对5个环境因子与液流速率进行相关分析，结果如表3。由表3可知，太阳总辐射量和光合有效辐射量分别与10 min后的液流速率相关系数增大，风速与20 min后的液流速率的相关系数也增大，因此液流速率相对于太阳总辐射量、光合有效辐射量和风速存在时滞效应，且时滞长度分别为 10 min、10 min 和 20 min。

表4 气象因子与液流速率的相关系数Table 4 Correlation coefficients between meteorological factors and sap flow velocity

利用考虑时滞效应的液流速率和环境因子数据建立BP-人工神经网络模型，软件对话框参数选择如上，经过292次迭代计算，系统收敛，计算结束。计算输入层各神经元与隐含层各神经元的连接权值、隐含层各神经元与输出层各神经元的连接权值分别如表1、2。液流速率拟合值与观测值的关系如图4。

图4 考虑滞后效应的神经网络拟合结果Fig.4 Fitted result of artif i cial neural network model with lag effect considered

由图4可知，在考虑液流相对于环境因子时滞效应的条件下，液流速率拟合值与观测值的回归方程的决定系数为0.944，相对于不考虑时滞效应有明显的提高，且从考虑滞后前后拟合值和观测值相对误差的比较中可知(图5)，考虑液流时滞效应的条件下液流速率拟合值与观测值相对误差处于± 5%和±10%之间的分别为41.177%和70.588%，数据波动幅度明显减小，说明在树干液流的模型建立中，液流的时滞是不容忽略的现象。

图5 考虑滞后前后相对误差比较Fig.5 Comparison of relative error with and without time lag effect considered

将8月22日的气象、茎流数据带入所建立的BP人工神经网络模型，模型的拟合结果如图6。拟合值与观测值回归方程的决定系数达到0.929，统计分析表明，相对误差处于± 5%和±10%之间的分别为55.932%和84.746%，从而说明该模型具有很好的通用性。

图6 模型预测结果Fig.6 Results of model predicting

3 结论与讨论

陈立欣等认为在土壤水分充足的条件下，树干液流与土壤湿度相关性较弱，植株液流是蒸腾的反映，利用液流来表示蒸腾受到越来越多的关注[1,2]。液流受环境因子的影响，但由于植株枝干的水容调节作用，液流相对于环境因子存在不同程度的时滞，这种现在往往被忽略。在环境因子与液流的定量关系表达中，多元线性回归是一种较为简单的模型[1]，但由于多元线性回归以最小二乘法为计算基础，当自变量间存在较强的相关性时，这种方法的适用性受到质疑[23-25]。BP人工神经网络是一个具有高度非线性的超大规模连续时间动力系统，它利用梯度下降法优化求解，具有自学习的功能。本文以环境因子作为输入层，以液流作为输出层，通过系统优化拟合了液流速 率随环境因子的变化特征，模型检验表明，BP人工神经网络具有很高的拟合精度。在考虑液流时滞效应的条件下，模型的拟合精度进一步提高，因此液流时滞是一个不容忽视的现象。

[14] Loustau D, Berbigier P, Roumagnac P, et al. Transpiration of a 64-year old maritime pine stand in PortugalⅠ . Seasonal course of water f l ux through maritime pine[J]. Oecologia, 1996,107∶33-42.

[15] 李晓峰, 徐玖平. 企业财务危机预警Rough-ANN 模型的建立及其应用 [J]. 系统工程理论与实践 ,2004 (10)∶ 8-14.

[16] 胡燕瑜 , 桂卫华 , 李勇刚 , 等 . 基于 BP 神经网络的熔融锌液流量检测 [J].有色金属 , 2003,55(3)∶143-146.

[17] 过仲阳 , 陈中原 , 李绿芊 , 等 . 人工神经网络技术在水质动态预测中的应用[J].华东师范大学学报∶ 自然科学版, 2001,1∶84-89.

[18] 蒋任飞, 阮本清, 韩宇平, 等.基于BP神经网络的参照腾发量预测模型[J].中国水利水电科学研究院学报, 2005,3(4)∶ 308-311.

[19] 曹文强 , 韩海荣 , 马钦彦 , 等 . 山西太岳山辽东栎夏季树干液流通量研究 [J]. 林业科学 , 2004, 40(2)∶ 174-177.

[20] 唐启义,冯明光. DPS数据处理系统-实验设计、统计分析及模型优化 [M]. 北京 ∶ 科学出版社 , 2006.

[21] 蔡甲冰 , 刘 钰 ,许 迪 , 等 . 基于通径分析原理的冬小麦缺水诊断指标敏感性分析 [J].水利学报 , 2008, 39(1)∶ 83-90.

[22] 谢恒星 , 张振华 , 杨润亚 , 等 . 龙爪槐树干液流相对于气象因子的滞后效应分析 [J].林业科学 , 2007, 43(5)∶ 106-110.

[23] 陈立欣 , 李湛东 , 张志强 , 等 . 北方四种城市树木蒸腾耗水的环境响应 [J]. 应用生态学报 , 2009, 20(12)∶ 2861-2870.

[24] 巩垠熙 , 高 原 , 仇 琪 , 等 . 基于遥感影像的神经网络立地质量评价研究[J]. 中南林业科技大学学报,2013,33(10)∶42-47.[25] 涂云燕, 彭道黎. 基于神经网络的森林蓄积量估测[J]. 中南林业科技大学学报 , 2012, 32(3)∶ 49-52.

Artif i cial neural network model for stem sap flow of Chinese pagoda tree considering effect of time delay

XΙE Heng-xing1,2, ZHANG Zhen-hua2
(1. Key Lab. for Eco-environment of Multi-river Wetland in Shaanxi Province, Weinan 714000, Shaanxi, China;2. College of Geography and Planning, Ludong University, Yantai 264025, Shandong, China)

Ιn Ludong University, the trunk sapfl ow of Sophora japonica f. pendula and the micro-environment were measured with AZ-M sapfl ow system made in USA and AXWG03 auto-weather station made in Australia. The applicability of BP-arti fi cial neural network model in the quantitative analysis for trunk sapfl ow and environmental factors were conducted, and thefi tting precision changes of BP-arti fi cial neural network model before and after considering the effect of liquid-phase on lagged effect of micro-environment of meteorological factor were compared. The results show that the sapfl ow velocity relative to total solar radiation, photosynthesis available radiation and wind speed had sapfl ow lagging time of 10 min, 10 min and 20 min intervals, respectively; Thefi tting precision of BP-arti fi cal neural network model considering time lag effect was improved signi fi cantly between environmental factors and trunk sap fl ow compared with traditional multiple linear regression model; The determining coef fi cients of the regressive equation betweenfi tted value got from arti fi cial neural network model with time lag effect considered or not and multiple linear regression model and measured value were 0.936, 0.866 and 0.831, respectively; The relative error betweenfi tted value and measured value of sapfl ow velocity were 41.177%, 35.849%, 30.189% and 70.588%, 62.264%, 31.527% between ±5% and±10%. The model fitting precision would be improved signi fi cantly considered with the time lag effect.

Chinese pagoda tree；BP-arti fi cial neural network model; multiple linear regression model;fi tting precision; lagging effect

S715.4

A

1673-923X(2013)12-0037-05

2013-04-08

国家自然科学基金资助项目（41271236）；陕西省教育厅科研计划项目（12JK0814）；渭南师范学院科研计划育苗项目（13YKP011）

谢恒星，博士，主要从事节水灌溉理论与新技术研究，E-mail：xiehengxing@nwsuaf.edu.cn

张振华，教授，硕士生导师，主要从事区域水土资源高效利用研究，E-mail：zhangzh71@163.com

[本文编校：吴 彬 ]

[1] 孟 平,张劲松,王鹤松, 等.苹果树蒸腾规律及其与冠层微气象要素的关系[J].生态学报,2005,25(5)∶1075-1081.

[2] 孙惠珍,周晓峰,康绍忠.应用热技术研究树干液流进展[J].应用生态学报,2004,15(6)∶1074-1078.

[3]Swanson R H. Significant historical developments in thermal methods for measuring sap flow in trees[J ] . Agricultural and Forest Meteorology, 1994,72∶113-132.

[4]刘奉觉 ,Edwards W. R. N.,郑世锴 ,等 .杨树树干液流时空动态研究[J].林业科学研究,1993,6(4)∶368-372.

[5]Dawson T E. Determining water use by trees and forests from isotopic, energy balance and transpiration analyses∶ The role of tree size and hydraulic lift[J]. Tree Physiology, 1996,16∶263-272.

[6] 严昌荣,Alec Downey,韩兴国,等.北京山区落叶阔叶林中核桃楸在生长中期的树干液流研究[J].生态学报,1999,19(6)∶ 793-797.

[7]Martin T A. Winter season tree sap f l ow and stand transpiration in an intensively-managed loblolly and slash pine plantation[J]. Journal of Sustainable Forestry, 2000,10 (1/ 2) ∶155-163.

[8]Kostner B, Biron P, Siegwolf R, et al. Estimates of water vapor flux and canopy conductance of scots pine at the tree level utilizing different xylem sap flow method[J]. Theoretical and Applied Climatology, 1996.53∶105-113.

[9]Giorio P, Giorio G. Sap f l ow of several olive trees estimated with the heat-pulse technique by continuous monitoring of a single gauge[J]. Environmental and Experimental Botany, 2003(49)∶ 9-20.

[10] Herzog K M, Thum R, Zweifel Roman, et al. Heat balance measurements-to quantify sap flow in thin stems only?[J]. Agricultural and Forest Meteorology, 1997(83)∶ 75-94.

[11] Ford C R, Carol E G, Robert J M, et al. Modeling canopy transpiration using time series analysis∶ A case study illustrating the effect of soil moisture def i cit on Pinus taeda[J]. Agricultural Forest Meteorology, 2005,130∶163-175.

[12] Philip G. Oguntunde, et al. Measurement and modeling of transpiration of a rain-fed citrus orchard under sub-humid tropical conditions[J]. Agricultural Water Management, 2007,87(2)∶200-208.

[13] Schulze E D, Cermak J, Matyssek R, et al. Canopy transpiration and water fluxes in the xylem of the trunk of Larix and Picea trees-A comparison of xylem flow, porometer and cuvette measurements[J]. Oecologia (Berlin) 1985,66∶475-483.