MPPT不调节母线电源系统稳定性分析

林文立 刘治钢 余恒

（北京空间飞行器总体设计部，北京 100094）

1 引言

最大功率点跟踪（MPPT）控制技术已经在国外多个低轨大功率卫星、电推进等卫星平台及深空探测器上得到越来越多的应用［1-2］，例如欧洲航天局的“火星快车”（Mars Express）、“金星快车”（Venus Express）［3］、罗塞塔号（Rossetta）［4］、信使号（Messenger）［5］、贝皮-科伦坡（Bepi-Colombo）［6］等均采用串联型MPPT 电源系统。然而，由于功率源与负载均为非线性，串联型MPPT 电源系统在太阳电池阵与太阳电池阵功率调节器（Array Power Regulator，APR）间存在母线电压振荡或跌落等不稳定现象［7］。文献［8］利用简化电压控制模型，对雷达卫星-2（RADARSAT-2）及 宇 宙-地 中 海（COSMOSkyMed）卫星电源电压控制环的稳定性进行了分析，具有一定代表性；而国内目前对于空间电源系统母线电压稳定性的研究还比较少。

本文提出一种MPPT 不调节母线电源系统拓扑结构，介绍了它的两域控制模式，建立了太阳电池阵源端与负载端稳态分析的等效电路模型，采用小信号等效分析方法，对系统稳定性进行分析，研究结果可为MPPT 控制技术在未来空间电源系统中应用提供设计参考。

2 电源系统拓扑及控制模式

图1所示为MPPT 不调节母线电源系统拓扑，主要由太阳电池阵、APR、控制电路、蓄电池组、负载等组成。根据发电端及负载端电压高低，APR 主电路可选择升压（或降压）直流-直流（DC-DC）变换器形式。其中，Ⅰload为负载电流；Ⅰbatt为蓄电池充／放电流；isa为太阳电池阵输出电流；vsa为太阳电池阵输出电压；vMEA为一次电源母线电压。

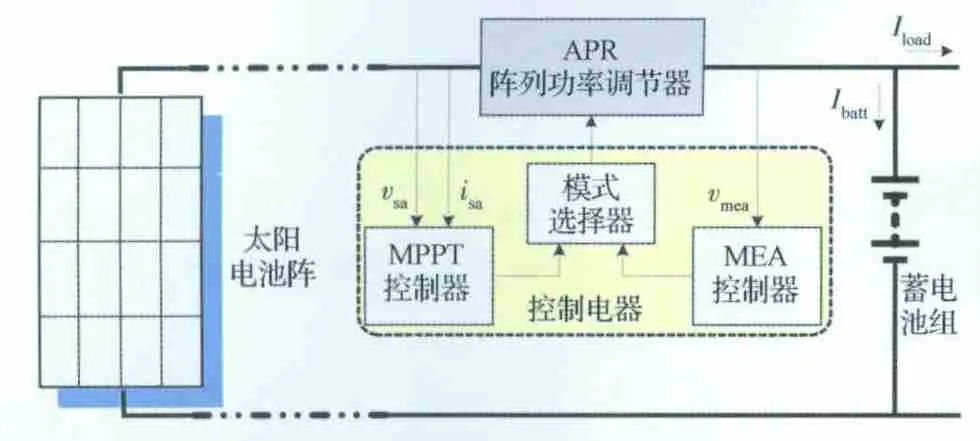
图1 MPPT 不调节母线电源系统拓扑Fig．1 Diagram of MPPT unregulated bus electrical power system topology

图1中，控制电路包括MPPT 控制器、主误差信号放大器（Main Error Amplifier，MEA）控制器、模式选择器等，通常设计为两域控制方式［9］，如图2所示，其中电压Va＜Vb＜Vc＜Vd，模式选择器根据负载功率需求及母线电压高低自主选择MPPT 控制模式或者MEA 控制模式，具体描述如下：当母线电压处于（Va，Vb）范围内，即负载功率需求大于太阳电池阵所能提供的电能时，模式选择器选择MPPT 控制模式，电源系统工作在MPPT 控制域，太阳电池阵始终跟踪最大功率点输出；当母线电压处于（Vc，Vd）范围内，即太阳电池阵所提供电能大于负载功率需求时，模式选择器选择MEA 控制模式，系统处于充电及电压控制域，控制电路根据电池充电特性调整母线电压值，当电池电压充满电后进行恒压控制，在此域范围内太阳电池阵根据负载及电池充电需要调整输出功率；（Vb，Vc）电压范围是控制系统所设置的迟滞区间，以避免在两种模式间频繁切换。

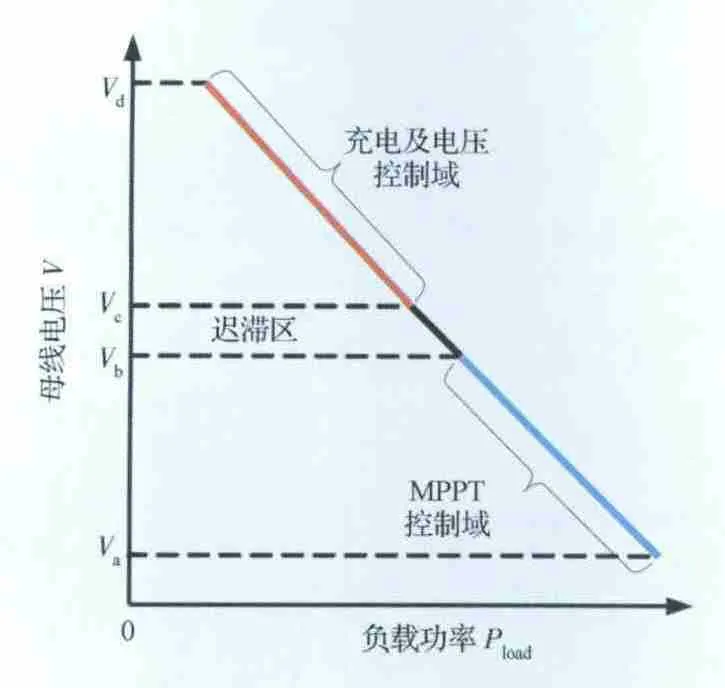
图2 MPPT 不调节母线电源系统的两域控制模式Fig．2 Two-domain control mode for MPPT unregulated bus electrical power system topology

3 电源系统稳定性分析

上文提到MPPT 不调节母线电源系统存在两域工作模式，因此，下面将分别针对两种工作模式进行电源系统的稳定性分析。

3．1 MPPT控制域下电源系统稳定性分析

在MPPT控制域下，太阳电池阵输出电压始终保持在最大功率点对应的电压值附近，因此APR 的输入端可认为是一个恒压源。图3（a）中太阳电池阵输出特性曲线与APR的输入特性（恒压源）曲线二者交点即为暂态工作点，建立MPPT 控制域下的等效电路模型，如图3（b）所示，图中左侧函数f（vsa）代表太阳电池阵的输出特性，vsa为太阳电池阵的输出电压，isa为太阳电池阵的输出电流，电容Csa为太阳电池阵寄生电容，Lline为线路寄生电感，iL为电感电流值，APR及后级负载均统一用恒压源VAPR代替，见图3（b）中右侧方框，其函数表达式为f（iL）。

根据图3（b），得到如下表达式：

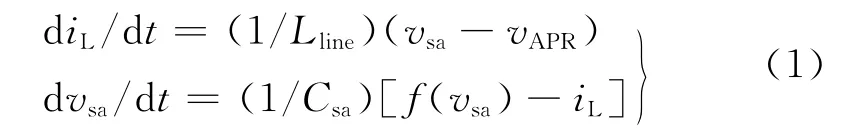
由于f（vsa）为非线性函数，设图3（a）中暂态工作点处电压稳态值为vsa，在此处添加小信号动态扰动值Δvsa，按泰勒级数的一阶线性展开［10］，得

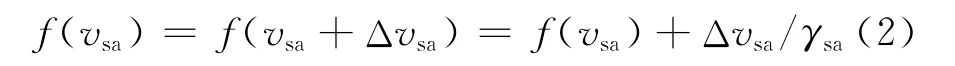
式中：γsa表示函数f（vsa）在某一特定太阳电池阵输出电压数值vsa时的微分值，因此，γsa＜0。

将式（2）代入式（1），得到其在暂态工作点处小信号线性状态空间表达式为

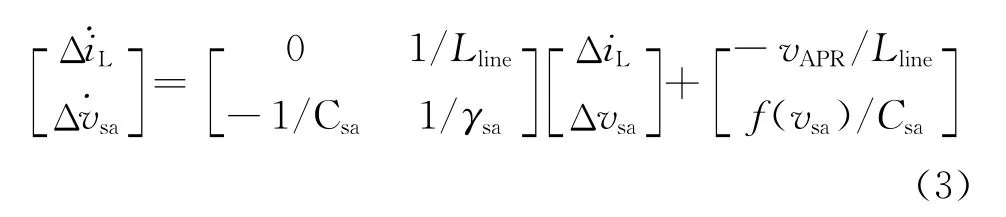
经计算，得到式（3）的特征根为

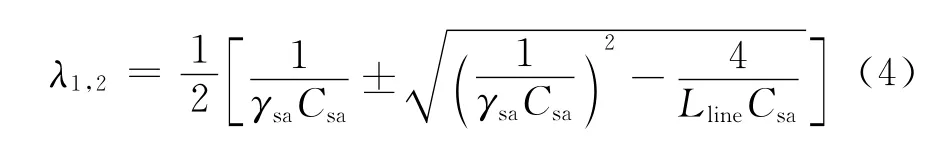
由于γsa＜0，因此式（4）中两个特征根λ1，2均为负值，根据李亚普诺夫稳定性定理［11］可知，该线性定常系统是稳定的，从而表明MPPT 不调节母线电源系统在MPPT 控制域下始终是保持稳定的。

图3 MPPT 控制域下源端与负载端特性曲线及稳态分析等效电路模型Fig．3 Source and load characteristics curves and stability analysis equivalent circuit model in MPPT control domain

3．2 充电及电压控制域下电源系统稳定性分析

在充电及电压控制域下，对一次母线进行恒压控制，因此，APR 的输入端呈现恒功率特性。图4（a）为充电及电压控制域下源端与负载端特性曲线，其中太阳电池阵输出特性曲线与APR 的输入特性（恒功率）曲线二者交点即为暂态工作点，建立充电及电压控制域下的等效电路模型，如图4（b）所示，图中APR 及后级负载均用恒功率特性曲线代替，见图4（b）中右侧方框。

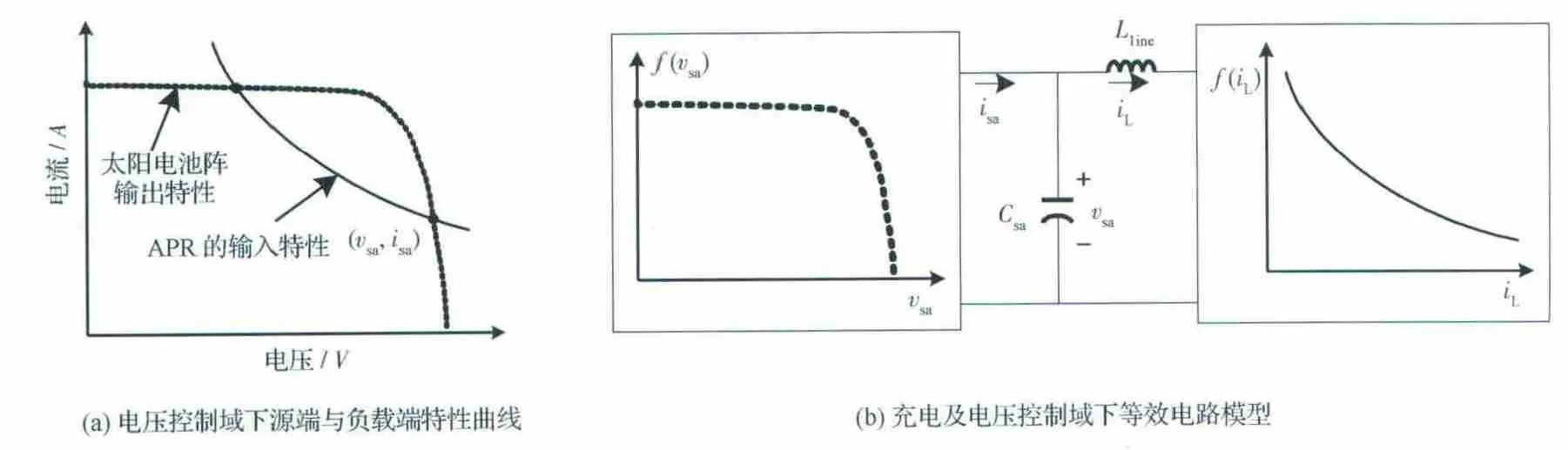
图4 充电及电压控制域下源端与负载端特性曲线及稳态分析等效电路模型Fig．4 Source and load characteristics curves and stability analysis equivalent circuit model in charging and voltage control domain

根据图4（b），得到如下表达式：

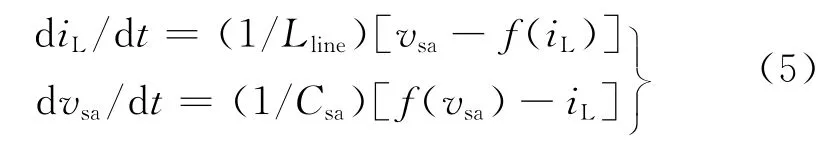
其中，f（vsa）、f（iL）均为非线性函数，设图4（a）中暂态工作点处电压稳态值为（vsa，isa），在暂态工作点处对f（vsa）、f（iL）分别添加小信号动态扰动值Δvsa、ΔiL，然后按泰勒级数的一阶线性展开，得其中，γAPR表示函数f（iL）在电感电流值为iL时的微分值。

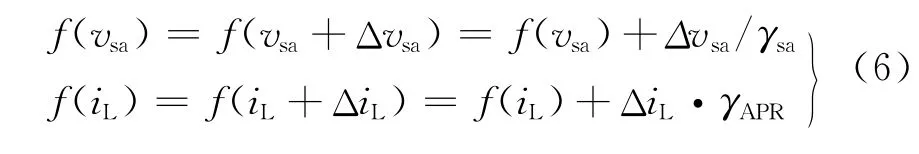
将式（6）代入式（5），得到其在暂态工作点处小信号线性状态空间表达式：

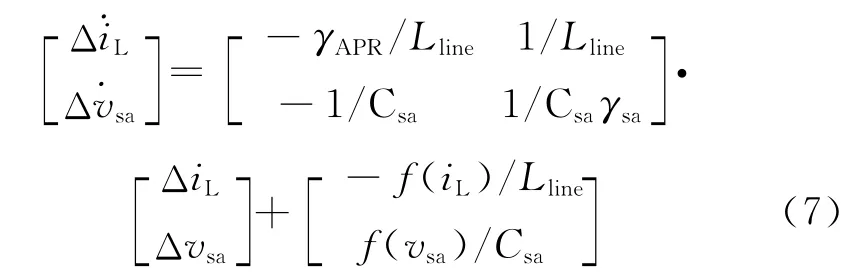
计算式（7）的特征根为

必须根据图4（a）中暂态工作点在太阳电池阵输出特性曲线的位置来判断系统的稳定性：

1）最大功率点左侧的电流源区段：γsa＜0，γAPR＜0并且∣γsa∣＜∣γAPR∣

在本区段范围内，无论γsa，γAPR，Csa，Lline的数值如何，λ1或λ2中至少有一个特征根为正数，即至少有一个特征根位于s平面右侧。根据李亚普诺夫稳定性定理可知，系统是不稳定的。

2）最大功率点右侧的电压源区段：γsa＜0，γAPR＜0并且∣γsa∣＞∣γAPR∣

在本区段范围内，当γsa·γAPR＜Lline／Csa时，λ1和λ2均为负数，根据李亚普诺夫稳定性定理可知，系统是稳定的；当γsa·γAPR＞Lline／Csa时，λ1和λ2均为正数，系统是不稳定的。

因此，在MPPT 不调节母线电源系统设计上，必须满足“γsa·γAPR＜Lline／Csa”的条件，才能保证电源系统在充电及电压控制域下的稳定性。

4 结论

本文提出一种MPPT 不调节母线电源系统拓扑结构，针对其两域控制模式，分别建立了太阳电池阵源端与负载端稳态分析的等效电路模型，采用小信号等效分析方法，对系统稳定性进行分析。

通过研究，得到以下结论：①无论源端与负载端特性曲线及电路参数如何设置，在MPPT 控制域内，电源系统始终保持稳定；②在充电及电压控制域内，电源系统的稳定与否是有条件限制的，即必须保证源端／负载端特性曲线及电路参数满足“γsa·γAPR＜Lline／Csa”的条件，才能保证电源系统稳定。

（References）

［1］刘治钢，蔡晓东，陈琦．采用MPPT 技术的国外深空探测器电源系统综述［J］．航天器工程，2011，20（5）：105-110

Liu Zhigang，Cai Xiaodong，Chen Qi．Overview of electrical power system design based on MPPT for deep space spacecraft［J］．Spacecraft Engineering，2011，20（5）：105-110（in Chinese）

［2］ESA．MPPC Regulated bus power system management for LEO and GEO missions［C］／／Proceedings of the 8th European Space Power Conference．Paris：ESA，2008：1-11

［3］Loche D．Mars Express and Venus Express power subsystem in-flight behaviour［C］／／Proceedings of the 8thEuropean Space Power Conference．Paris：ESA，2008：1-7

［4］Fiebrich H，Haines J，Tonicello F．Power system design of the Rosetta spacecraft［C］／／Proceedings of the 2nd IECEC．Washington D．C．：AIAA，2004：1-7

［5］Dakermanji G，Person C，Jenkins J．The Messenger spacecraft power system design and early mission performance［C］／／Proceedings of the 7th European Space Power Conference．Paris：ESA，2005：1-8

［6］Maset E，Sanchis-Kilders E，Weinberg A H．Ion drive propulsion MPP power conditioning system without battery［C］／／Proceedings of the 8th European Space Power Conference．Paris：ESA，2008：239-247

［7］Usman L，Shakeel B．Stability study of spacecraft electrical power system with constant-power loads［C］／／Proceedings of the 14th International Multitopic Conference．New York：IEEE，2011：217-221

［8］Luciano C，Paolo D，Alberto L．Maximum power point tracker point controller for unregulated bus architecture［C］／／Proceedings of the 7th European Space Power Conference．Paris：ESA，2005：1-6

［9］蔡晓东，刘治钢，张明，等．混合式MPPT 星载电源系统拓扑设计与仿真分析［J］，航天器工程，2013，22（3）：77-82

Cai Xiaodong，Liu Zhigang，Zhang Ming，et a1．Design and simulation of a mixed MPPT electrical power system topology［J］．Spacecraft Engineering，2013，22（3）：77-82（in Chinese）

［10］王宇宾，常鲜戎，罗艳，等．基于隐式Taylor级数法的电力系统暂态稳定计算［J］．华北电力大学学报，2005，32（2）：1-6

Wang Yubin，Chang Xianrong，Luo Yan，et al．An implicit Taylor series method for simulation of power system transient［J］．Journal of North China Electric Power University，2005，32（2）：1-6（in Chinese）

［11］奚国华，沈红平，喻寿益，等．基于全阶状态观测器的无速度传感器DTC系统［J］．电气传动，2008，38（7）：22-25

Xi Guohuang，Shen Hongping，Yu Shouyi，et al．Speed sensorless DTC system based on full-order state observer［J］．Electric Drive，2008，38（7）：22-25 （in Chinese）