六面体小微卫星散热面最优化设计

黄金印 赵欣 麻慧涛 刘庆志

（北京空间飞行器总体设计部 空间热控技术北京市重点实验室，北京 100094）

1 引言

小微卫星具有体积小、质量轻、研制成本较低等特点，目前已经成为空间飞行器领域的重要组成部分，尤其是以编队飞行或者星座组网方式的小微卫星受到越来越多的重视［1-4］。随着卫星体积和质量的不断减小，小微卫星热控制技术将受到较大挑战。一方面，可供热控系统使用的重量和功耗资源相对常规大卫星更加紧张；另一方面，由于小微卫星星上电子设备的高度集成，整星功率体积比密度变大，可能导致局部热流密度较大而导致局部温度较高；此外，由于小微卫星热容量小、比表面积大，更容易受到空间外热流的影响，导致整星温度水平波动较大。文献［5］对国内外部分小微卫星失效原因的分析结果表明：由于上述不利因素的影响，因而造成的热控系统整星失效数占所有小微卫星失效数的34%左右，远高于其它系统或者单机产品。因此，探索适应小微卫星自身特点的热控设计方法十分必要。

吴文瑞等［6］以某太阳同步轨道卫星正六棱柱形卫星为例，建立以热控系统多层隔热材料质量最小为目标的最优化设计模型，对多层隔热材料厚度及卫星散热面面积进行了优化设计。王玉莹等［7］以某太阳同步轨道球形纳卫星为例，采用混沌遗传算法对工作在不同热负荷下的纳卫星散热面面积和多层隔热组件厚度进行了优化设计。上述两个模型都是基于某一固定降交点地方时的太阳同步轨道卫星，外热流环境较为稳定。而对于倾斜轨道卫星以及编队或星座组网方式飞行的小微卫星，通常整个寿命期间卫星各个表面到达的外热流变化十分剧烈，并且卫星各个表面都有可能受到太阳直照，使得卫星没有单一、稳定的散热面。为了解决这一问题，宁献文、赵欣等［8-9］建立了倾斜轨道六面体卫星极端外热流的解析模型，并以此为基础提出了一种针对倾斜轨道、三轴稳定对地定向的六面体卫星的组合式散热面优化设计方法。该方法将卫星的六个表面的散热面分为X型散热面和Y型散热面；通过选择不同的散热面组合方式，得到不同散热面组合方式下卫星吸收总外热流随β角（阳光与轨道面的夹角）的变化规律，从而确定最佳的散热面组合方式。然而，由于选取的组合方式有限并且散热面类型划分较粗，优化设计的结果仍然有一定的局限性。

为了探索应用范围更广的散热面最优化设计方法，本文首先建立基于六面体卫星的散热面最优化设计模型，并以某倾斜轨道六面体小微卫星为例，在详细分析其各面到达外热流随β角变化规律的基础上系统介绍了散热面最优化设计方法。

2 六面体小微卫星散热面优化设计模型

2．1 简化假设

对于给定轨道参数的卫星，其参与的换热过程，包括空间外热流对卫星的加热、卫星内部设备热耗、卫星自身不同设备之间的辐射和导热换热以及卫星向宇宙空间的辐射换热等部分，因此对于卫星表面任意节点i，其与空间环境及卫星内部的换热如下［10］：

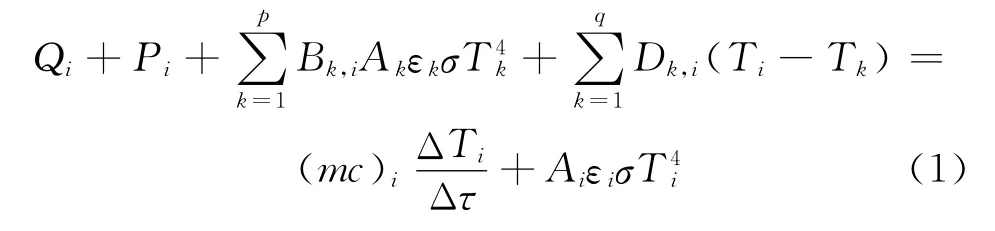
式中：Qi为节点i吸收的空间外热流；Pi为节点i的内热源；Bk，i为节点k辐射的能量被节点i吸收的部分；Dk，i为节点k和节点i之间的热导；Ai为节点i的面积，（mc）i为节点i的热容；ε为表面的红外发射率；σ为玻尔兹曼常数；T为节点温度；τ为时间。

当系统达到热平衡状态后，对整个卫星有

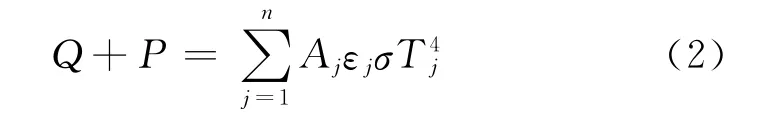
式中：Q为卫星各表面吸收的总外热流；P为卫星总热耗；Aj为卫星第j个外表面的面积。假设卫星外表面除了散热面以外的部位均包覆多层隔热组件，且忽略卫星通过多层隔热组件和空间环境的换热，则式（2）表示卫星吸收空间外热流和整星热耗之和等于卫星通过散热面向空间环境的散热量。

卫星各表面吸收的外热流受β角、太阳辐射的强度、地球反照热流、地球的辐射热流、表面涂层光学参数等众多因素的影响，为了方便建立优化设计模型，采用如下简化假设［8，10］：

（1）虽然一年中冬至日附近的太阳辐射的强度和夏至日附近有6．9%左右的差别，但是在进行极端外热流的理论分析时可忽略这部分变化，认为太阳辐射的强度不随季节变化；

（2）卫星表面状态包括多层隔热组件和散热面两种。对于多层表面，由于其良好的隔热效果，多层表面吸收外热流量级很小，理论分析时忽略这部分影响，仅考虑散热面吸收的外热流；

（3）考虑到卫星在轨道周期内的热惯性，以及地球反照辐射及红外辐射相对于太阳辐射而言比例较小，因此计算中取恒定的地球平均反照系数和平均地球红外辐照，忽略β角变化对于二者所带来的影响。

2．2 优化目标

为了使用最少的热控功耗满足任务需求，热设计过程中需要在保证整星温度水平合理的前提下，通过合理选择散热面的位置和组织星内换热，尽量减小散热面面积。由式（2）可知，影响散热面面积的因素包括空间外热流和卫星内部功耗。卫星内部功耗通常受到设备布局和整星工作模式的限制，因此，进行卫星散热面优化设计的一个有效途径是，根据外热流环境合理选择不同表面散热面面积，从而使不同空间环境下散热面吸收的空间外热流最小。

对于六面体小微卫星，卫星各散热面吸收总外热流Q（β）可以表示为

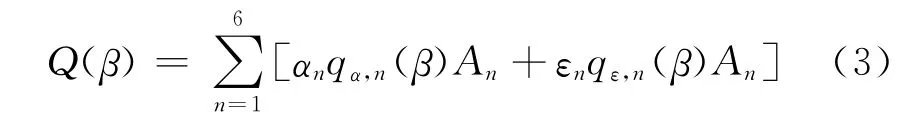
式中：n为六面体卫星各面编号；An为卫星第n个表面的散热面面积；qα，n（β）为到达散热面的太阳直照外热流和地球反照热流之和随β角变化的函数；qε，n（β）为到达散热面的地球红外热流随β角变化的函数。

对于β角在一定范围内变化的卫星，为了使得吸收空间外热流最小，要求所选择的散热面组合方式使得在该区间内的任意一个β角处，散热面吸收空间外热流在不同散热面组合方式中达到最小。这里，该任意β角可表示为βi。若将β角的变化范围l等分，则βi可以描述为

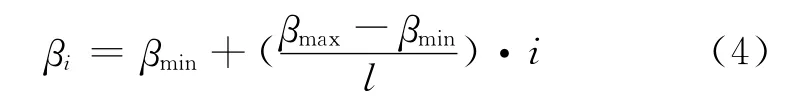
式中：βmin为β角的最小值；βmax 为β角的最大值。

2．3 问题约束

最优化的散热面设计受到几方面因素的影响：首先，各散热面散热能力应保证将卫星内部产生的热耗排散至星外，如式（5）所示；其次，卫星各表面散热面面积受到该表面能够提供作为热控散热面面积的限制，如式（6）所示。

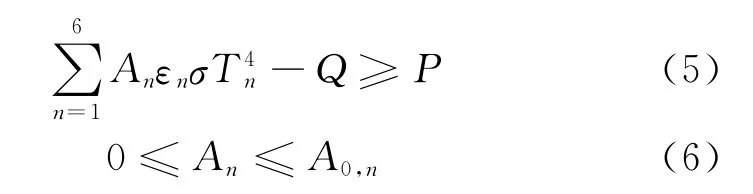
式中：A0，n为卫星第n个表面的面积。

2．4 优化设计模型

综合以上分析，六面体小微卫星散热面最优化设计问题可以抽象为［11］

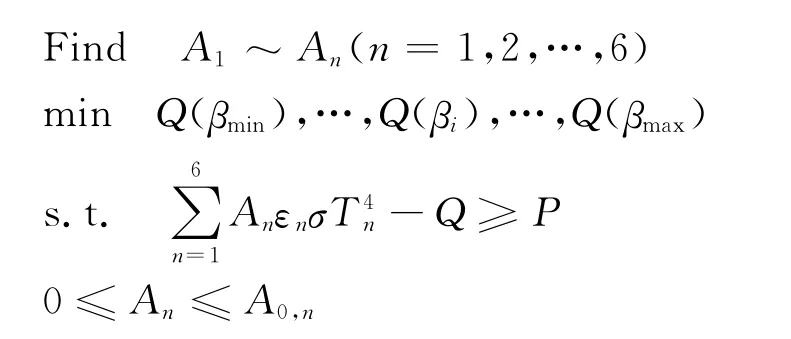
3 应用实例

本节以某倾斜轨道六面体卫星为例，验证上述优化设计模型的合理性。

3．1 算例简介

该六面体卫星尺寸为1m×1m×1m，轨道高度800km，轨道倾角66．5°，轨道偏心率为0。卫星飞行姿态为三轴稳定，＋Z轴对地定向，＋X轴指向飞行方向，＋Y轴由右手定则确定。

图1、图2分别给出了该卫星各表面到达太阳直照外热流和地球反照热流随β角的变化趋势，采用最小二乘法可以拟合出各面到达太阳直照外热流和地球反照热流关于β角的函数。地球红外热流不随β角变化，如表1所示。此外，卫星热耗为100～350 W。为了方便计算各散热面的散热能力，各散热面的平均温度设置为-10 ℃。

表1 不同β角下卫星各表面到达地球红外热流Table 1 Arriving earth IR heat flux on the satellite surfaces

3．2 优化结果

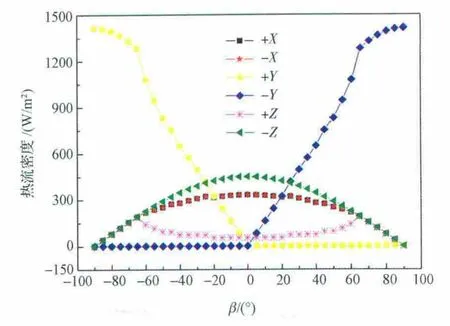
图1 各表面到达太阳直照外热流随β角的变化规律Fig．1 Variation of the arriving solar heat flux on the satellite surfaces versusβ

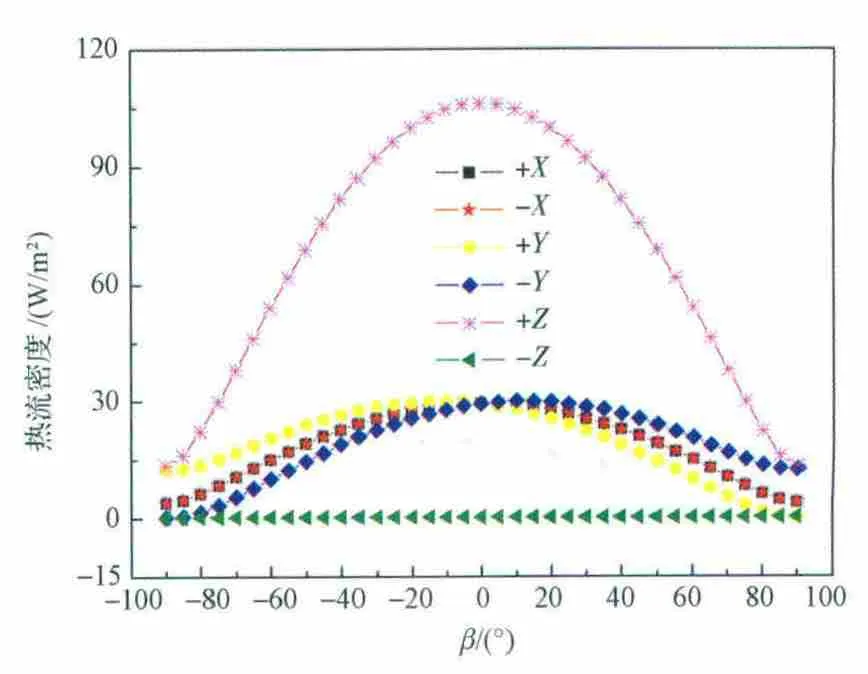
图2 各表面到达地球反照外热流随β角的变化规律Fig．2 Variation of the arriving albedo heat flux on the satellite surfaces versusβ

调用Matlab软件的多目标优化函数fgoalattain，分别得到整星热耗（P）为100 W、150 W、200 W、250 W、300 W 和350 W 时该六面体卫星的最优化散热面布局及对应散热面布局下卫星各散热面吸收总热流随β角的变化规律（图3）。

由图3可知，当｜β｜≤70°时，对于给定的整星热耗，整星各散热面吸收的总外热流随β角的变化很小，这将显著减小由于外热流变化造成的整星温度波动；当70°≤｜β｜≤90°时，散热面吸收总热流相对小β角时迅速减小。由图1可知，随着β角的变化，到达±Y面的太阳辐射热流变化最为剧烈。为了减小整星散热面总吸收外热流随β角的变化，布置在±Y面的散热面面积相对较小。当70°≤｜β｜≤90°时，随着β角的增大，除＋Y（或-Y）面以外，卫星其余各面基本到达的外热流迅速降低，直至完全不受照，因此整星散热面吸收的总热流迅速减小。

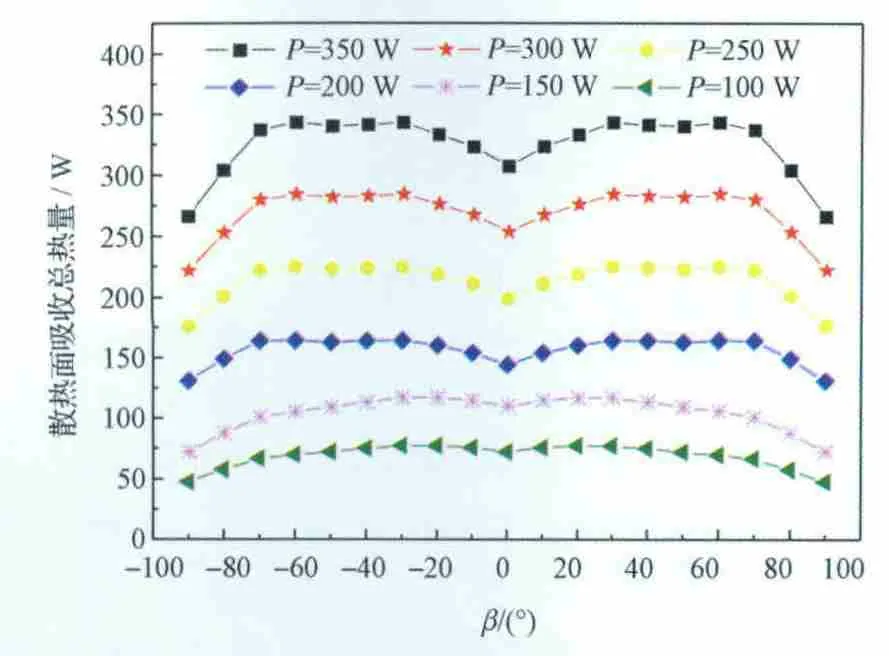
图3 散热面吸收总外热流随β角的变化规律Fig．3 Variation of the total absorbed external heat flux versusβ

图4给出了卫星各表面最优散热面面积随整星热耗的变化规律。如图4所示，最优化的散热面布局随着整星热耗水平的增加而变化，但卫星-Z面是整星最理想的主散热面；随着整星热耗的增加，±Y面散热面面积呈近似线性增大。由图1和图2可知，±Y面到达的太阳直照热流和地球红外热流关于β＝0°对称，并且±Y面外热流随β角的变化规律与其他四个表面相反。因此，为了有效降低卫星吸收总外热流随β的变化，必需在±Y面布置一定面积的散热面；±X面到达太阳外热流随β的变化较剧烈，并且受到较强的地球反照热流和红外热流的照射，当整星热耗较小时，不宜选择±X面作为散热面；当整星热耗较大时，随着整星热耗的增加，±X面散热面面积显著增加，说明对于热耗较大的卫星±X面是较理想的辅助散热面；＋Z面始终对地，受到的地球红外热流最大，并且到达地球反照热流随β的变化也比较剧烈，因此一般不宜作为散热面。

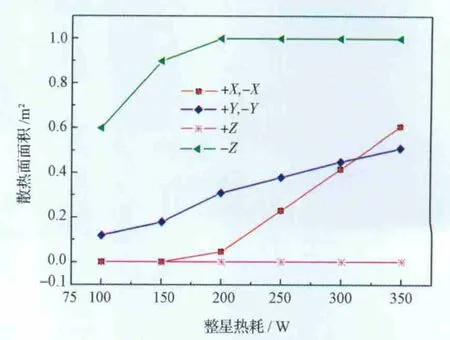
图4 各表面散热面面积随整星热耗的变化规律Fig．4 Variation of the radiator area versus the heatload of satellite

3．3 优化设计方法讨论

一般来说，传统的散热面布局方式往往需要多次迭代并且十分依赖工程经验，而本文所述最优化设计方法仅需根据卫星寿命期间β角的变化范围进行外热流分析，然后在Matlab软件中调用多目标优化设计函数，进行一轮计算即可得到最优化的散热面布局，大大地节省了散热面设计的时间。

根据应用实例及优化结果可知，采用本文最优化方法得到的最优化散热面布局与文献［8-9］所得到的散热面分布规律完全一致。需要进一步指出的是，在实际卫星设计时，需要将设备热负荷布局与本文最优化设计方法结合起来。基于该方法设计的散热面，某长期功耗约为100 W 的小微卫星，整个寿命期间散热面最大吸收外热流和最小吸收外热流的差值仅为15 W 左右，有效地降低了寿命初期整星的补偿功耗。

4 结束语

本文建立了六面体卫星散热面最优化设计模型，并以某倾斜轨道六面体小微卫星为例、调用多目标优化函数针对不同卫星热耗分别得出了最优化的散热面布局，给出了一种基于外热流分析的确定卫星最优化散热面布局的数学方法。分析结果表明：采用本文所述的最优化设计方法得到的散热面布局，可以有效降低由于外热流变化造成的整星温度波动；对于不同的热耗水平，整星最优化散热面布局不完全相同，采用本文所述方法可以为散热面设计提供有力支持。虽然本文算例选取的是β角在±90°之间变化的倾斜轨道六面体小微卫星，但是设计方法和最优化模型对β角变化较小的太阳同步轨道和地球同步轨道同样具有参考意义。

（References）

［1］麻慧涛，钟奇，范含林，等．微型卫星热控制技术研究［J］．航天器工程，2006，15（2）：6-13

Ma Huitao，Zhong Qi，Fan Hanlin，et al．Investigation of the thermal control technology for micro-satellite［J］．Spacecraft Engineering，2006，15（2）：6-13 （in Chinese）

［2］Volodymyr B．Micro-satellites thermal control-concepts and components［J］．Acta Astronautica，2005，56（1-2）：161-170

［3］Elhady A M．Design and analysis of a LEO micro-satellite thermal control including thermal contact conductance［J］．2010IEEE Aerospace Conference．New York：IEEE，2010：1-11

［4］刘佳，李运泽，常静，等．微小卫星热控系统的研究现状及发展趋势［J］．航天器环境工程，2011，28（1）：77-82

Liu Jia，Li Yunze，Chang Jing，et al．A review of small satellite thermal control system［J］．Spacecraft Environment Engineering，2011，28（1）：77-82（in Chinese）

［5］徐济万．小卫星应用与热控系统研究［C］／／第五届空间热物理会议．北京：中国宇航学会，2002：367-376

Xu Jiwan．Research on small satellite application and thermal control system［C］／／5th China Space Thermophysics Conference．Beijing：Chinese Society of Astronautics，2002：367-376（in Chinese）

［6］吴文瑞，黄海．太阳同步轨道卫星热控分系统分析及优化［J］．航天器工程，2012，21（2）：44-49

Wu Wenrui，Huang Hai．Analysis and optimization of SSO satellite thermal control subsystem［J］．Spacecraft Engineering，2012，21（2）：44-49（in Chinese）

［7］王玉莹，李运泽，刘东晓．纳卫星隔热层厚度与散热面面积优化设计［J］．航天器工程，2010，19（2）：46-51

Wang Yuying，Li Yunze，Liu Dongxiao．Optimized design of heat insulation layers’thickness and radiator surfaces for nano-satellite［J］．Spacecraft Engineering，2010，19（2）：46-51（in Chinese）

［8］宁献文，张加迅，江海，等．倾斜轨道六面体卫星极端外热流解析模型［J］．宇航学报，2008，29（3）：754-759

Ning Xianwen，Zhang Jiaxun，Jiang Hai，et al．Extreme external heat flux analytical model for inclined-orbit hexahedral satellite［J］．Journal of Astronautics，2008，29（3）：754-759（in Chinese）

［9］宁献文，赵欣，杨昌鹏．倾斜轨道卫星组合式散热面优化设计方法［J］．航天器工程，2012，21（5）：48-52

Ning Xianwen，Zhao Xin，Yang Changpeng．Optimum design method of combined type radiator for inclined-orbit satellite［J］．Spacecraft Engineering，2012，21（5）：48-52（in Chinese）

［10］侯增祺，胡金刚．航天器热控制技术——原理与应用［M］．北京：中国科学技术出版社，2007：347-351

Hou Zengqi，Hu Jingang．Spacecraft thermal control technology—theory and application［M］．Beijing：China Science and Technology Press，2007：347-351（in Chinese）

［11］李元科．工程最优化设计［M］．北京：清华大学出版社，2006：121-125

Li Yuanke．Optimization principles and techniques for engineering design［M］．Beijing：Tsinghua University Press，2006：121-125（in Chinese）